Published online by Cambridge University Press: 12 March 2014
We presuppose the terminology of [1], and we give a negative answer to the following problem ([1], p. 19): Does every essentially undecidable axiomatizable theory have an essentially undecidable finitely axiomatizable subtheory?
We use the following theorem of Kleene ([2], p. 311). There exist two recursively enumerable sets α and β such that (1) α and β are disjoint (2) there is no recursive set η for which α ⊂ η, β ⊂ η′. By the definition of recursive enumerability, there are recursive predicates Φ and Ψ for which
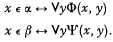
We now specify a theory T which will afford a counter-example to the given problem of Tarski. The only non-logical constants of T are two binary predicates P and Q, one unary operation symbol S, and one individual constant 0. As in ([1], p. 52) we define
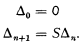
The only non-logical axioms of T are the formulae P(Δm, Δn) for all pairs of integers m, n satisfying Δ(m, n); the formulae Q(Δm, Δn) for all pairs of integers m, n satisfying Ψ(m, n); and the formula
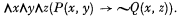
T is consistent, since it has a model. It remains to show that (1) every consistent extension of T is undecidable (2) if T1 is a finitely axiomatizable subtheory of T, there exists a consistent and decidable extension of T1 which has the same constants as T1.