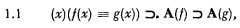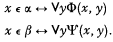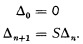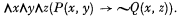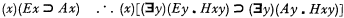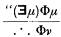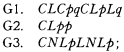Research Article
A new approach to semantics – Part I
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-27
-
- Article
- Export citation
Two concepts from the theory of models1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 28-32
-
- Article
- Export citation
Note on a problem of L. Henkin
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 33-35
-
- Article
- Export citation
On the axiom of extensionality – Part I
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 36-48
-
- Article
- Export citation
Solution of a problem of Tarski
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 49-51
-
- Article
- Export citation
Another variant of natural deduction
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 52-55
-
- Article
- Export citation
Reduction to a symmetric predicate
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 56-59
-
- Article
- Export citation
Modality and quantification in S5
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 60-62
-
- Article
- Export citation
Formal systems of constructive mathematics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 63-75
-
- Article
- Export citation
Reviews
Leonard Linsky. Preface. Semantics and the philosophy of language, A collection of readings, edited by Leonard Linsky, The University of Illinois Press, Urbana1952, pp. vii–viii. - Leonard Linsky. Introduction. Semantics and the philosophy of language, A collection of readings, edited by Leonard Linsky, The University of Illinois Press, Urbana1952, pp. 3–10.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 76
-
- Article
- Export citation
Alfred Tarski. The semantic conception of truth and the foundations of semantics. A reprint of IX 68 (with omission of the Spanish abstract). Semantics and the philosophy of language, A collection of readings, edited by Leonard Linsky, The University of Illinois Press, Urbana1952, pp. 13–47. - C. I. Lewis. The modes of meaning. A reprint of IX 28 (with omission of the Spanish abstract). Semantics and the philosophy of language, A collection of readings, edited by Leonard Linsky, The University of Illinois Press, Urbana1952, pp. 50–63. - Nelson Goodman. On likeness of meaning. A revision of XV 150(2). Semantics and the philosophy of language, A collection of readings, edited by Leonard Linsky, The University of Illinois Press, Urbana1952, pp. 67–74.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 76-77
-
- Article
- Export citation
Willard V. Quine. Notes on existence and necessity. A reprint of VIII 45. Semantics and the philosophy of language, A collection of readings, edited by Leonard Linsky, The University of Illinois Press, Urbana1952, pp. 77–91. - Bertrand Russell. Descriptions. A reprint of Chapter XVI of 11126. Semantics and the philosophy of language, A collection of readings, edited by Leonard Linsky, The University of Illinois Press, Urbana1952, pp. 95–108. - Benson Mates. Synonymity. A reprint of XIX 223(1). Semantics and the philosophy of language, A collection of readings, edited by Leonard Linsky, The University of Illinois Press, Urbana1952, pp. 111–136. - Paul Marhenke. The criterion of significance. Semantics and the philosophy of language, A collection of readings, edited by Leonard Linsky, The University of Illinois Press, Urbana1952, pp. 139–159. (Reprinted from Proceedings and addresses of The American Philosophical Association, vol. 23 (1950).)
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 77-78
-
- Article
- Export citation
Carl G. Hempel. Problems and changes in the empiricist criterion of meaning. A reprint of XVI 293(1). Semantics and the philosophy of language, A collection of readings, edited by Leonard Linsky, The University of Illinois Press, Urbana1952, pp. 163–185. - Willard V. Quine. On what there is. A reprint of XV 152(2). Semantics and the philosophy of language, A collection of readings, edited by Leonard Linsky, The University of Illinois Press, Urbana1952, pp. 189–206. - Rudolf Carnap. Empiricism, semantics, and ontology. A reprint of XVI 292(5). Semantics and the philosophy of language, A collection of readings, edited by Leonard Linsky, The University of Illinois Press, Urbana1952, pp. 208–228. - Nelson Goodman. The problem of counterfactual conditionals. A reprint of XII 139(1). Semantics and the philosophy of language, A collection of readings, edited by Leonard Linsky, The University of Illinois Press, Urbana1952, pp. 231–246. - Arne Næss. Toward a theory of interpretation and preciseness. A reprint of XV 154(1). Semantics and the philosophy of language, A collection of readings, edited by Leonard Linsky, The University of Illinois Press, Urbana1952, pp. 248–269. - Morton G. White. The analytic and synthetic: an untenable dualism. A reprint of XVI 210. Semantics and the philosophy of language, A collection of readings, edited by Leonard Linsky, The University of Illinois Press, Urbana1952, pp. 272–286. - Leonard Linsky. Bibliography. Semantics and the philosophy of language, A collection of readings, edited by Leonard Linsky, The University of Illinois Press, Urbana1952, pp. 287–289. - Nelson Goodman. On likeness of meaning. A reprint of XV 150(2). Philosophy and analysis, A selection of articles published in Analysis between 1933–40 and 1947–53, edited by Margaret Macdonald; Basil Blackwell, Oxford1954, and Philosophical Library, New York 1954; pp. 54–62. Foreword (added 1954), pp. 54–55. - Nelson Goodman. On some differences about meaning. Philosophy and analysis, A selection of articles published in Analysis between 1933–40 and 1941–53, edited by Margaret Macdonald; Basil Blackwell, Oxford1954, and Philosophical Library, New York 1954; pp. 63–69. (Reprinted from Analysis, vol. 13 no. 4 (1953), pp. 90–96; see Corrections, ibid., vol. 13 no. 6 (1953), p. 144.) - Paul Wienpahl. More about denial of sameness of meaning. Analysis (Oxford), vol. 12 no. 1 (1951), pp. 19–23. - J. F. Thomson. Some remarks on synonymy. Analysis (Oxford), vol. 12 no. 3 (1952), pp. 73–76. - C. D. Rollins. Sameness of meaning—reply to Mr. Wienpahl and others. Analysis (Oxford), vol. 13 no. 2 (1952), pp. 46–48. - Richard Rudner. A note on likeness of meaning. Analysis (Oxford), vol. 10 no. 5 (1950), pp. 115–118. - Beverly Levin Robbins. On synonymy of word-events. Analysis (Oxford), vol. 12 no. 4 (1952), pp. 98–100. - F. H. George. Meaning and class. Analysis (Oxford), vol. 13 no. 6 (1953), pp. 135–140. - Lester Meckler. On Goodman's refutation of synonymy. Analysis (Oxford), vol. 14 no. 3 (1954), pp. 68–78.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 78-82
-
- Article
- Export citation
L. J. Cohen and A. C. Lloyd. Assertion-statements. Analysis (Oxford), vol. 15 no. 3 (1955), pp. 66–70.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 82-83
-
- Article
- Export citation
S. Korner. Truth as a predicate. Analysis (Oxford), vol. 15 no. 5 (1955), pp. 106–109.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 83
-
- Article
- Export citation
Paul Weiss. The paradox of necessary truth. Philosophical studies, vol. 6 (1955), pp. 31–32.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 83
-
- Article
- Export citation
Yehoshua Bar-Hillel. Mr. Weiss on the paradox of necessary truth. Philosophical studies, vol. 6 (1955), pp. 92–93.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 83
-
- Article
- Export citation
Friedrich Waismann. Analytic—synthetic. Analysis (Oxford), vol. 10 (1949–1950), pp. 25–40, and vol. 11 (1950–1), pp. 25–38, 49–61, 115–124, and vol. 13 (1952–3), pp. 1–14, 73–89.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 84-85
-
- Article
- Export citation
Beryl Lake. Necessary and contingent statements. Analysis (Oxford), vol. 12 no. 5 (1952), pp. 115–122. - Peter G. Winch. Necessary and contingent truths. Analysis (Oxford), vol. 13 no. 3 (1953), pp. 52–60.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 85
-
- Article
- Export citation
Max Black. The identity of indiscernibles. Mind, n.s. vol. 61 (1952), pp. 153–164. Reprinted with minor changes in: Problems of analysis, Philosophical essays, by Max Black, Cornell University Press, Ithaca 1954, pp. 80–92, 292–293. - Gustav Bergmann. The identity of indiscernibles and the formalist definition of “identity.”Mind, n.s. vol. 62 (1953), pp. 75–79. - N. L. Wilson. The identity of indiscernibles and the symmetrical universe. Mind, n.s. vol. 62 (1953), pp. 506–511. - A. J. Ayer. The identity of indiscernibles. Actes du XIème Congrès International de Philosophie, Volume III, Métaphysique et ontologie, North-Holland Publishing Company, Amsterdam1953, and Éditions E. Nauwelaerts, Louvain 1953, pp. 124–129. Reprinted in Philosophical essays by A. J. Ayer, St. Martin's Press, New York 1954, and Macmillan & Co., London 1954, pp. 26–35. - D. J. O'Connor. The identity of indiscernibles. Analysis (Oxford), vol. 14 no. 5 (1954), pp. 103–110. - Nicholas Rescher. The identity of indiscernibles: A reinterpretation. The journal of philosophy, vol. 52 (1955), pp. 152–155. - D. Pears. The identity of indiscernibles. Mind, n.s. vol. 64 (1955), pp. 522–527.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 85-86
-
- Article
- Export citation