One of the main goals in the theory of forcing iteration is to formulate preservation theorems for not collapsing ω1 which are as general as possible. This line leads from c.c.c. forcings using finite support iterations to Axiom A forcings and proper forcings using countable support iterations to semi-proper forcings using revised countable support iterations, and more recently, in work of Shelah, to yet more general classes of posets. In this paper we concentrate on a special case of the very general iteration theorem of Shelah from [5, chapter XV]. The class of posets handled by this theorem includes all semi-proper posets and also includes, among others, Namba forcing.

In [5, chapter XV] Shelah shows that, roughly, revised countable support forcing iterations in which the constituent posets are either semi-proper or Namba forcing or P[W] (the forcing for collapsing a stationary co-stationary subset of

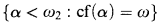
with countable conditions) do not collapse ℵ1. The iteration must contain sufficiently many cardinal collapses, for example, Levy collapses. The most easily quotable combinatorial application is the consistency (relative to a Mahlo cardinal) of ZFC + CH fails + whenever A ∪ B = ω2 then one of A or B contains an uncountable sequentially closed subset. The iteration Shelah uses to construct this model is built using P[W] to “attack” potential counterexamples, Levy collapses to ensure that the cardinals collapsed by the various P[W]'s are sufficiently well separated, and Cohen forcings to ensure the failure of CH in the final model.

In this paper we give details of the iteration theorem, but we do not address the combinatorial applications such as the one quoted above.

These theorems from [5, chapter XV] are closely related to earlier work of Shelah [5, chapter XI], which dealt with iterated Namba and P[W] without allowing arbitrary semi-proper forcings to be included in the iteration. By allowing the inclusion of semi-proper forcings, [5, chapter XV] generalizes the conjunction of [5, Theorem XI.3.6] with [5, Conclusion XI.6.7].