Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T00:50:33.360Z Has data issue: false hasContentIssue false
  • English
  • Français

Set-theoretic foundations for logic

Published online by Cambridge University Press:  12 March 2014

W. V. Quine
Get access Rights & Permissions [Opens in a new window]

Extract

1. Introduction. In his set theory Zermelo uses the variables “x”, “y”, etc. for the representation of “things” generally. Among these things he includes sets, or, as I shall say henceforth, classes. He adopts the connective “ϵ” of membership as his sole special primitive; thus the elementary formulae of his system are describable simply as expressions of the form “xϵy”, with any thing-variables ”x”, “y”, “z”, etc. supplanting “x” and “y”. The postulates of his system are so fashioned as to avoid the logical paradoxes without use of the theory of types. One of the postulates, the so-called Aussonderungsaxiom, may be stated in familiar logical notation as

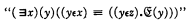
where 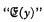is understood as any statement about y which is definite in a certain sense which Zermelo introduces informally for the purpose. Skolem has pointed out that it is adequate here to construe “definite” statements as embracing just the elementary formulae and all formulae thence constructible by the truth functions and by quantification with respect to thing-variables. A second of Zermelo's postulates is the principle of extensionality; this asserts that mutually inclusive classes are identical, i.e. are members of just the same classes. There are further postulates which provide for the existence of the null class, the class of all subclasses of any given class, the class of all members of members of any given class, the unit class of any given thing, and the class whose sole members are any two given things. Finally the multiplicative axiom (Auswahlprinzip) and the axiom of infinity are adopted.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 1 , Issue 2 , June 1936 , pp. 45 - 57
Copyright
Copyright © Association for Symbolic Logic 1936

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

2 Zermelo, , Grundlagen der Mengenlehre I, Mathematische Annalen, vol. 65 (1908), pp. 261–281CrossRefGoogle Scholar.

3 See Skolem, , Einige Bemcrkungen zu der Abhandlung von E. Zermelo: “Über die Definitheit in der Axiomatik”, Fundamenta mathematicae, vol. 15 (1930), pp. 337–341CrossRefGoogle Scholar.

4 Whitehead and Russell, Principia mathematica, 2nd. edition.

5 Vol. 2, p. 183; vol. 1, p. 481.

6 See Łukasiewicz, and Tarski, , Utiterstichungen über den Aussagenkalkül, Comptes rendus Soc. Sci. et Let. de Varsovie, vol. 23 (1930), Classe III , p. 34 (reprint p. 6), Satz 6Google Scholar.

7 See Quine, , Truth by convention, Philosophical essays for A. N. Whitehead (Lee, O. H., editor; New York, 1936), pp. 107–112, esp. note 18Google Scholar.

8 Tarski, , Einige Betrachtungen über die Begriffe der ω-Widerspruchsfreikeit und der ω-Vollsändigkeit, Monatshefte für Mathematik und Physik, vol. 40 (1933), p. 103, Def. 9. Note that “Fr(θ)” here is a misprint for “Fr(η)”Google Scholar.

9 See Łukasiewicz and Tarski, op. cit., p. 42 (reprint p. 14), Satz 30.

10 See P.M., vol. 1, pp. xiii, xvi.

11 See P.M., vol. 1, p. xvi.

12 See Łukasiewicz, , Uwagi o aksyomacie Nicod'a i o “dedukcyi uogólniajqcej,” Ksiega pamiqtkowa Polskiego Towarzystwa Filozowicznego we Lwowie (Lwów, 1931), pp. 2–7Google Scholar.

13 Op. cit., pp. 97–103. My formulation departs from Tarski in inessential respects, largely notational.

14 Tarski, op. cit., p. 97.

15 Wiener, , A simplification of the logic of relations, Proceedings of the Cambridge Philosophical Society, vol. 17 (1914), pp. 387–390Google Scholar.

16 Kuratowski, , Sur la notion de l'ordre dans la théorie des ensembles, Fundamenta mathematicae, vol. 2 (1920), p. 171Google Scholar.

17 See the next to the last formula in the proof of Lemma 3, below.

18 This is the basis of the proof of Lemma 5, below.

19 See P.M., vol. 1, p. xiii. Indeed, Tarski has revised Δ in just this fashion in Der Wakrheitsbegriff in den formalisierten Sprachen, Studia philosophica, vol. 1 (1935), pp. 365–366, 291–299Google Scholar.