Article contents
Post completeness in modal logic
Published online by Cambridge University Press: 12 March 2014
Extract
Let ⊥, →, and □ be primitive, and let us have a countable supply of propositional letters. By a (modal) logic we understand a proper subset of the set of all formulas containing every tautology and being closed under modus ponens and substitution. A logic is regular if it contains every instance of □A ∧ □B ↔ □(A ∧ B) and is closed under the rule

A regular logic is normal if it contains □⊤. The smallest regular logic we denote by C (the same as Lemmon's C2), the smallest normal one by K. If L and L' are logics and L ⊆ L′, then L is a sublogic of L', and L' is an extension of L; properly so if L ≠ L'. A logic is quasi-regular (respectively, quasi-normal) if it is an extension of C (respectively, K).
A logic is Post complete if it has no proper extension. The Post number, denoted by p(L), is the number of Post complete extensions of L. Thanks to Lindenbaum, we know that

There is an obvious upper bound, too:

Furthermore,
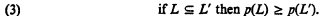 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1972
References
REFERENCES
- 12
- Cited by


