Article contents
On the reduction of the decision problem. Third paper. Pepis prefix, a single binary predicate
Published online by Cambridge University Press: 12 March 2014
Extract
It has been proved by Pepis that any formula of the first-order predicate calculus is equivalent (in respect of being satisfiable) to another with a prefix of the form
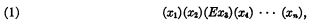
containing a single existential quantifier. In this paper, we shall improve this theorem in the like manner as the Ackermann and the Gödel reduction theorems have been improved in the preceding papers of the same main title. More explicitly, we shall prove the
Theorem 1. To any given first-order formula it is possible to construct an equivalent one with a prefix of the form (1) and a matrix containing no other predicate variable than a single binary one.
An analogous theorem, but producing a prefix of the form
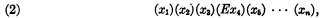
has been proved in the meantime by Surányi; some modifications in the proof, suggested by Kalmár, led to the above form.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1950
References
1 See Annales de la Société Polonaise de Mathématique, vol. 18 (1945), p. IIIGoogle Scholar.
2 Pepis, Józef, Ein Verfahren der mathematischen Logik, this Journal, vol. 3 (1938), pp. 61–76Google Scholar; Untersuchungen über das Entscheidungsproblem der mathematischen Logik, Fundamenta mathematicae, vol. 30 (1938), pp. 257–348CrossRefGoogle Scholar, especially theorems 35, 37, 38, and 40, pp. 325–340.
3 As a matter of fact, Pepis has constructed for any given first-order formula an equivalent one of the form (x1)(x2)(Ex3)N(x1, x2, x3)& (x4)…(xn)N′(x4, …, xn) (N and N′ containing no quantifiers), which can be brought into the prenex form
but also into the prenex form
4 Kalmár, László, On the reduction of the decision problem, first paper, Ackermann prefix, a single binary predicate, this Journal, vol. 4 (1939), pp. 1–9Google Scholar; László Kalmár and János Surányi, On the reduction of the decision problem, second paper, Gödel prefix, a single binary predicate, ibid., vol. 12 (1947), pp. 65–73. We shall quote these papers as “first paper,” “second paper.”
5 János Surányi, A logikai függvénykalkulus eldöntésproblémájának redukciójáról (in Hungarian with German abstract: Zur Reduktion des Entscheidungsproblems des logischen Funktionenkalküls), Matematikai és fizikai lapok, vol. 50 (1943), pp. 51–74Google Scholar, especially theorem 2, pp. 65–73, and in the abstract, p. 74.
6 Surányi's theorem (loc. cit.) is a consequence of Theorem 1, for a formula having a prefix of the form (1) can be changed, by attaching the quantifier (x 0) before (x 1) with a variable x 0 not occurring in the formula, into another with a prefix of the form (2).
7 Surányi (loc. cit.) supposes that A has a prefix of the form (1) (and, as a matter of fact, n = 4, which does not involve any loss of generality, as shown in the same paper; see a forthcoming paper of Surányi with the same main title as that of the present one, fifth paper). The use of the theorem of the first paper, suggested by Kalmár, allows some simplifications but is not absolutely necessary to reach the prefix (1) instead of (2).
8 See e. g. Skolem, Th., Über einige Grundlagenfragen der Mathematik, Skrifter utgitt av det Norske Videnskaps-Akademi i Oslo, mat.-naturv. klasse, 1929, no. 4, pp. 1–49, especially §4Google Scholar. In the first paper, it has been shown that to every satisfiable first-order formula there is another, A, of the above form, which can be satisfied in the above way.
9 We shall omit the adjective “positive” unless we wish to emphasize it.
10 This idea to replace existential quantifiers by universal ones was used also by Pepis (loc. cit.). We think, it takes its origin from Skolem, Th., Logisch-kombinatorische Untersuchungen über die Erfüllbarkeit oder Beweisbarkeit mathematischer Säize nebst einem Theorem über dichte Mengen, Videnskapsselskapets skrifter, Kristiania, mat.-naturv. klasse, 1920, no. 4, pp. 1–36, especially pp. 4–6Google Scholar.
11 Had we not supposed that A contains a single predicate variable, we would have had to characterize here each of the predicates forming together a satisfying system for A (as elements of J) by means of a predicate expressed by ψ. This we could do similarly as we did in the second paper. Surányi (loc. cit.) proceeds also in this way. In the case of a single predicate, this reduces to the characterization of Φ by means of the predicate ψ (x, x).
12 For simplicity, we omit the conjunction sign, or we replace it by a dot.
13 Instead of this, we could also define ψ (x, y) for integers x, y to hold if and only if y differs from x as well as from x + 1. By means of the ψ defined thus, the predicates “y = x + 1” and “y = x” could be expressed respectively as ![]() and
and ![]() .
.
14 The sign Π stands for conjunction.
15 We regard a conjunction abbreviated by the sign Π as a single member.
16 I. e., if the antecedent of (8) holds; similarly for (9), (10), (11a), (11b), (12), and, later on, for (8′a), (8′b), (9′), (10′), and (11′).
17 Also (x 0)(x 1)(Ez)(x 2)(x 3) … (xn)(p 11)(p 12) … (pnn)(N1(G; x 0, …, x n, p 11, p 12, …, pnn)N2(G; x 0, x 1, z, x 2, x 3)) is a prenex formula equivalent to B.
18 The range of the variables being J again.
19 See footnote 16.
20 Also (x 0)(x 1)(Ez)(x 2)(x 3)… (x n)(p 11)(p 12) … (p nn)(N′1(G; x 0,…, x n, p 11, p 12, …, p nn)N′2(G; x 0, x 1, z, x 2)) is a prenex formula equivalent to B′.
21 Indeed, the descriptive function attached to the existential quantifier in (3) has n − 1 arguments, while that corresponding to (1) has two arguments only.
22 In the case of the first variant, the structure of (10) prevents us from performing an analogous modification.
- 6
- Cited by


