Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kaye, Richard
1990.
Diophantine Induction.
Annals of Pure and Applied Logic,
Vol. 46,
Issue. 1,
p.
1.
Adamowicz, Z.
and
Dimitracopoulos, C.
1991.
On A Problem Concerning Parameter Free Induction.
Mathematical Logic Quarterly,
Vol. 37,
Issue. 23-24,
p.
363.
Clote, P.
and
Takeuti, G.
1992.
Bounded arithmetic for NC, ALogTIME, L and NL.
Annals of Pure and Applied Logic,
Vol. 56,
Issue. 1-3,
p.
73.
Fernández‐Margarit, A.
and
Pérez‐Jiménez, M. J.
1994.
Maximum Schemes in Arithmetic.
Mathematical Logic Quarterly,
Vol. 40,
Issue. 3,
p.
425.
Beklemishev, Lev D.
1999.
Parameter free induction and provably total computable functions.
Theoretical Computer Science,
Vol. 224,
Issue. 1-2,
p.
13.
Buss, S.
1999.
1998 European Summer Meeting of the Association for Symbolic Logic.
Bulletin of Symbolic Logic,
Vol. 5,
Issue. 1,
p.
59.
Moniri, Morteza
2003.
Independence results for weak systems of intuitionistic arithmetic.
Mathematical Logic Quarterly,
Vol. 49,
Issue. 3,
p.
250.
Беклемишев, Лев Дмитриевич
and
Beklemishev, Lev Dmitrievich
2005.
Схемы рефлексии и алгебры доказуемости в формальной арифметике.
Успехи математических наук,
Vol. 60,
Issue. 2,
p.
3.
Cordón-Franco, Andrés
Fernández-Margarit, Alejandro
and
Lara-Martín, F. Félix
2005.
Fragments of Arithmetic and true sentences.
Mathematical Logic Quarterly,
Vol. 51,
Issue. 3,
p.
313.
Cordón–Franco, Andrés
and
Lara–Martín, F. Félix
2012.
How the World Computes.
Vol. 7318,
Issue. ,
p.
440.
Visser, Albert
2014.
Peano Corto and Peano Basso: A Study of Local Induction in the Context of Weak Theories.
Mathematical Logic Quarterly,
Vol. 60,
Issue. 1-2,
p.
92.
Cordón-Franco, A.
Fernández-Margarit, A.
and
Lara-Martín, F. F.
2014.
On axiom schemes for T-provably $${\Delta_{1}}$$ Δ 1 formulas.
Archive for Mathematical Logic,
Vol. 53,
Issue. 3-4,
p.
327.
Visser, Albert
2015.
The Arithmetics of a Theory.
Notre Dame Journal of Formal Logic,
Vol. 56,
Issue. 1,
Hetzl, Stefan
and
Vierling, Jannik
2023.
Induction and Skolemization in saturation theorem proving.
Annals of Pure and Applied Logic,
Vol. 174,
Issue. 1,
p.
103167.
Kurahashi, Taishi
and
Minami, Yoshiaki
2024.
On collection schemes and Gaifman's splitting theorem.
Mathematical Logic Quarterly,
Vol. 70,
Issue. 4,
p.
398.


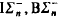 (induction and collection schemas for parameter free
(induction and collection schemas for parameter free 