Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-03T02:36:11.912Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on truth-tables

Published online by Cambridge University Press:  12 March 2014

Jan Kalicki
Jan Kalicki*
Affiliation:
University of Leeds
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper a method will be described which is intended to exhibit some relationships between sets of tautologies determined by truth-tables. This method is an attempt to form an algebra of truth-tables. The results sketched below are restricted to sets of tautologies determined by truth-tables with a finite number of elements and involving a single binary connective Δ. However, most of the results can be easily extended to the case of Tarski's logical matrix and even to a more general case.

We denote by S(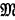) the set of all tautologies (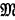-tautologies) according to a given truth-table 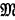. Let 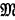describe a binary connective Δ. Then Δ(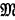)(x, y) stands for the truth-value of ΔPQ, when P has the truth-value x and Q has the truth-value y. If no ambiguity may arise we write Δ(x, y) or Δ(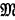) for Δ(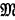)(x, y).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 15 , Issue 3 , September 1950 , pp. 174 - 181
Copyright
Copyright © Association for Symbolic Logic 1950

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 For the definition of the logical matrix see Łukasiewicz, J. and Tarski, A., Untersuchungen über den Augsagenkalkül, Comptes rendus des séances de la Société des Sciences et des Lettres de Varsovie, vol 23 (1930), def. 3, p. 33Google Scholar.

2 See the author's On Tarski's matrix method, forthcoming in the Comptes rendus des séances de la Société des Sciences et des Lettres de Varsovie.

3 See Wajsberg, M., Beiträge zum Metaaussagenkalkül I, Monatshefte für Mathematik und Physik, vol 42 (1935), p. 241Google Scholar.

4 See Tarski, A., Der Aussagenkalkül und die Topologie, Fundamenta mathematicae, vol. 31 (1938), def. 2.3 and cor. 2.7CrossRefGoogle Scholar.

5 For a definition see Lukasiewicz, J., Elementy logiki matematycznej, Warsaw 1929, pp. 116–120Google Scholar.

6 See the author's A test for the existence of tautologies according to many-valued truth-tables, in this number of this Journal.

7 We call a w.f.f. W the shortest in a set S if there is no Y ϵ S which can be written by means of a smaller number of signs than W. There may be many W's with this property.

8 See J. Łukasiewicz and A. Tarski, op. cit.