Published online by Cambridge University Press: 12 March 2014
Professor C. I. Lewis, in Lewis and Langford's Symbolic logic, designates the system (S2) determined by the postulates used in Chapter VI—namely, 11.1–7 (B1–7) and

as the system of strict implication. For certain reasons, he prefers it to either the earlier system (S3) determined by the stronger set of postulates of his Survey of symbolic logic, as emended, namely, A1–7 and
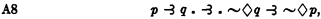
or the system (S1) determined by the weaker set of postulates B1–7 or A1–7.
But Lewis and others, following O. Becker, have also given consideration to systems which contain some additional principle effecting the reduction of complex modalities to simpler ones. Notable are the system (S4) determined by B1–7 plus
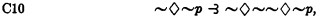
which includes (is stronger than) S3; and the system (S5) determined by B1–7 plus

which includes S4.
It seems worth while to investigate further the system of the Survey (emended), S3, which is intermediate between S2 and S4. This is the purpose of the present paper. We first prove some additional theorems in S2 and S3. These enable us to reduce all the complex modalities in S3 to a finite number, viz. 42; and it is shown that no further reduction is possible. Finally, several systems which include S3 are considered.
1 We shall leave out of account the existence postulate 20.01 (B9) of Symbolic logic, which may be considered either as present in all of the systems to be discussed or as absent in all of them.
2 Op. cit., pp. 177f., 496.
3 Zur Logik der Modalitäten, Jahrbuch für Philosophie und phänomenologische Forschung, vol. 11 (1930), pp. 497–548Google Scholar.
4 McKinsey, J. C. C., A reduction in number of the postulates for C. I. Lewis's system of strict implication, Bulletin of the American Mathematical Society, vol. 40 (1934), pp. 425–427CrossRefGoogle Scholar.
5 Proceedings of the American Academy of Arts and Sciences, vol. 72 (1937), pp. 1–44CrossRefGoogle Scholar; cited in this paper as “Huntington.”
6 An alternative set of postulates for S3 is obtained by adding to the postulates for S2 the principle
proved below as a theorem of S3. 30.1 (A8) can then be proved, as follows:
The same effect would of course be produced by adding any of the principles
etc., instead of 31.12.
This postulate set provides a sort of analysis of S3 in comparison with 82, making clearer just what S3 involves. 31.12, it seems to me, is as intuitively evident, is as acceptable a principle of deduction, as any of the postulates of S2 (or at least, as any of those of the second degree, i.e., B6–8; see note 11 below). It may profitably be compared with the principle of replacement of equivalents, according to which, for example, if P−Q, then (since ∼◇∼P=∼◇∼P=∼◇∼P=∼◇∼Q.
7 Churchman, C. W., On finite and infinite modal systems, this Journal, vol. 3 (1938), pp. 77–82Google Scholar; see pp. 79f.
8 Theorems 31.2–.32, 31.5–32.31 are contained in my doctoral thesis, Implication, on file in the Harvard University Library.
9 Cf. Wajsberg, M., Ein erweiterter Klassenkalkül, Monatshefte für Mathematik und Physik, vol. 40 (1933), pp. 113–126, especially pp. 115f, and Sätze 1–3, pp. 118fCrossRefGoogle Scholar. For the proof of Satz 1.6,18.53 p⊰q·∼◇∼p:⊰·∼◇∼q may be used instead of Wajsberg's Axiom e (corresponding to our 31.11).
10 Cf. O. Becker, op. cit.; Feys, R., Les Logiques nouvelles des modalités, Revue néoscolastique de philosophie, vol. 40 (1937), pp. 517–553, vol. 41 (1938), pp. 217–252,—especially no. 21 (p. 532f)CrossRefGoogle Scholar; Parry, W. T., Zum Lewisschen Aussagenkalkül, Ergebnisse eines mathematischen Kolloquiums, Heft 4 (1933), pp. 15–16Google Scholar.
11 More generally, the degree of a modal function is defined thus: (1) The propositional variables p, q, r, … are of zero degree. (2) If P is of degree n, then ∼P is of degree n, and (3) ◇P is of degree n+1. (4) If P is of degree n, and Q of degree m, where n≥m, then the degree of P·Q and of Q·P is n. (5) Any function equivalent by definition to a function of degree n is also of degree n.
12 This reduction may be checked by constructing a “tree” of A-modalities, substituting alternately -1p, -2p for p, in p and in every resultant of this process, ending a “branch” at each modality which reduces to one of lower degree. The branches end at the following modalities: -1-2-2p; -1-1-1-1p, -1-1-1-2p, -1-1-2-2p, -1-2-1-1p, -1-2-1-2p; -1-1-2-1-1p, -1-1-2-1-2p; -2-2p; -2-1-2p; -2-1-1-1p, -2-1-1-2p, each of which reduces to one of the ten given above, by: 32.95; 32.31.33.96.97.82; 32.98.84;32.9; 32.91;32.92.93, respectively.
13 Ex. 0.4 is the writer's example in The postulates for “strict implication”, Mind, vol. 43 (1934), pp. 78–80Google Scholar, introduced to distinguish S2 from S3, with different designation of the elements.
The definition may be expressed thus: Let the elements be understood as designating classes. 1 = the universe class, composed of the mutually exclusive classes 4, 6, and 7. The complements of 1, 4, 6, 7 are designated by 8, 5, 3, 2 respectively. Then p·q = the logical product of p and q; and ∼p = the complement of p (making the system a Boolean algebra).
14 Cf. Becker, op. cit., I, §2.
15 This fact is mentioned but not proved in Symbolic logic, p. 501.
16 There are implications, however. For example, any affirmative (or negative) modality of type A implies any affirmative (or negative, respectively) of type B; any affirmative (or negative) of type C implies any affirmative (or negative, respectively) of type D.
17 Op. cit., §3 (pp. 512–517).
18 Symbolic logic, p. 498. The proof of this fact, by the way, was first pointed out to me by Mr. Y. T. Shen.
19 Churchman (op. cit., pp. 78–81) has shown that S5 is obtained by adding to S2 the principle C15′ p⊰∼◇◇∼◇p.
S5 is notable as reducing all modal functions to those of the first (or zero) degree—for which an Entscheidungsverfahren has been given: M. Wajsberg, op. cit.; W. T. Parry, Zum Lewisschen Aussagenkalkül, loc. cit.
20 Op. cit., 29.2–4. Feys' postulates 29.41 (corresponding to our 32.2) and 29.42 in this “logique tt” are redundant.
The total number of possibly distinct modalities of degrees 0 through n is (2+22+23+…2n+1=) 2n+2−2. Feys' “logique tt” therefore has a maximum of 14 distinct modalities.
21 Actually Feys states his principles with material implication (or equivalence) as the main relation; this can then be made into a strict relation by means of his rule of procedure 25.2—our 41.2.
If we add to S1 the postulates
corresponding to Feys 29.43, and 51.1 ![]() , then C11 follows, thus:
, then C11 follows, thus:
51.1 follows (by 22.3) from C12, which corresponds to Feys 28.31. Therefore Feys' “logique ss” (29.5), formed by adding Feys 28.31 to his “logique tt,” reduces to his “logique à modalités simples,” i.e., S5.
22 Becker, op. cit., Bemerkung zu §2 (p. 518f.).
23 Churchman, op. cit., pp. 78, 81n.