Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2025-01-03T18:22:53.205Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximal chains in the Turing degrees

Published online by Cambridge University Press:  12 March 2014

C. T. Chong  and
Liang Yu
C. T. Chong
Affiliation:
Department of Mathematics, Faculty of Science, National University of Singapore, Lower Kent Ridge Road, Singapore 117543, Singapore. E-mail: [email protected]
Liang Yu
Affiliation:
Institute of Mathematical Science, Nanjing University, Nanjing, Jiangsu Province 210093 PR. OF China. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the problem of existence of maximal chains in the Turing degrees. We show that:

1. ZF + DC + “There exists no maximal chain in the Turing degrees” is equiconsistent with ZFC + “There exists an inaccessible cardinal”

2. For all a ∈ 2ω, (ω1)L[a] = ω1 if and only if there exists a 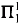[a] maximal chain in the Turing degrees. As a corollary, ZFC + “There exists an inaccessible cardinal” is equiconsistent with ZFC + “There is no (bold face) 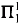maximal chain of Turing degrees”.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 72 , Issue 4 , December 2007 , pp. 1219 - 1227
Copyright
Copyright © Association for Symbolic Logic 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Abraham, Uri and Shore, Richard A., Initial segments of the degrees of size ℵ1, Israel journal of Mathematics, vol. 53 (1986), no. 1, pp. 1–51.CrossRefGoogle Scholar
[2]Barwise, Jon, Admissible Sets and Structures, Springer-Verlag, Berlin, 1975.CrossRefGoogle Scholar
[3]Boolos, George and Putnam, Hilary, Degrees of unsolvability of constructible sets of integers, this Journal, vol. 33 (1968), pp. 497–513.Google Scholar
[4]Devlin, Keith J., Constructibility, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1984.CrossRefGoogle Scholar
[5]van Engelen, Fons, Miller, Arnold W., and Steel, John, Rigid Borel sets and better quasiorder theory, Logic and Combinatorics (Areata, California, 1985), Contemporary Mathematics, vol. 65, American Mathematical Society, Providence, RI, 1987, pp. 199–222.CrossRefGoogle Scholar
[6]Jech, Thomas, Set Theory, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
[7]Jensen, R. B., The fine structure of the constructible hierarchy, Annals of Mathematical Logic, vol. 4 (1972), pp. 229–308, erratum, ibid. 4 (1972), 443.CrossRefGoogle Scholar
[8]Lerman, Manuel, Degrees of Unsolvability, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1983, Local and global theory.CrossRefGoogle Scholar
[9]Martin, D. A., Borel determinacy. Annals of Mathematics (2), vol. 102 (1975), no. 2, pp. 363–371.CrossRefGoogle Scholar
[10]Martin, D. A. and Solovay, R. M., Internal Cohen extensions, Annals of Mathematical Logic, vol. 2 (1970), no. 2, pp. 143–178.CrossRefGoogle Scholar
[11]Miller, Arnold W., Infinite combinatorics and definability, Annals of Pure and Applied Logic, vol. 41 (1989), no. 2, pp. 179–203.CrossRefGoogle Scholar
[12]Moschovakis, Yiannis N., Descriptive Set Theory, Studies in Logic and the Foundations of Mathematics, vol. 100, North-Holland Publishing, Amsterdam, 1980.Google Scholar
[13]Sacks, Gerald E., Degrees of Unsolvability, Princeton University Press, Princeton, N.J., 1963.Google Scholar
[14]Sacks, Gerald E., Higher Recursion Theory, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1990.CrossRefGoogle Scholar
[15]Simpson, Stephen G., Minimal covers and hyperdegrees, Transactions of the American Mathematical Society, vol. 209 (1975), pp. 45–64.CrossRefGoogle Scholar
[16]Solovay, Robert M., On the cardinality of sets of reals, Foundations of Mathematics (Symposium commemorating Kurt Gödel, Columbus, Ohio, 1966), Springer, New York, 1969, pp. 58–73.Google Scholar
[17]Solovay, Robert M., A model of set-theory in which every set of reals is Lebesgue measurable. Annals of Mathematics (2), vol. 92 (1970), pp. 1–56.CrossRefGoogle Scholar