Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-04T21:25:32.479Z Has data issue: false hasContentIssue false
  • English
  • Français

Intrinsic bounds on complexity and definability at limit levels

Published online by Cambridge University Press:  12 March 2014

John Chisholm ,
Ekaterina B. Fokina ,
Sergey S. Goncharov ,
Valentina S. Harizanov ,
Julia F. Knight  and
Sara Quinn
John Chisholm
Affiliation:
Department of Mathematics, Western Illinois University, Macomb, Il 61455, USA, E-mail: [email protected]
Ekaterina B. Fokina
Affiliation:
Kurt Gödel Research Center for Mathematical Logic, University of Vienna, Währinger Strasse 25, A-1090 Wien, Austria, E-mail: [email protected]
Sergey S. Goncharov
Affiliation:
Sobolev Institute of Mathematics, Siberian Branch of Ras, 4 Acad, Koptyug Ave. 630090 Novosibirsk, Russia, E-mail: [email protected]
Valentina S. Harizanov
Affiliation:
Department of Mathematics, George Washington University, Government Hall, Room 220, Washington, Dc 20052, USA, E-mail: [email protected]
Julia F. Knight
Affiliation:
Department of Mathematics, University of Notre Dame, 255 Hurley Hall, Notre Dame, In 46556, USA, E-mail: [email protected]
Sara Quinn
Affiliation:
Department of Mathematics, Northwestern University, 2033 Sheridan Road, Evanston, Il 60208-2730, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

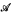We show that for every computable limit ordinal α, there is a computable structure that is 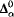categorical, but not relatively 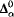categorical (equivalently, it does not have a formally 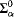Scott family). We also show that for every computable limit ordinal α, there is a computable structure 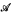with an additional relation R that is intrinsically 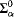on 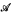, but not relatively intrinsically 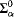on 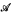(equivalently, it is not definable by a computable Σα formula with finitely many parameters). Earlier results in [7], [10], and [8] establish the same facts for computable successor ordinals α.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 74 , Issue 3 , September 2009 , pp. 1047 - 1060
Copyright
Copyright © Association for Symbolic Logic 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ash, C. J., A construction for recursive linear orderings, this Journal, vol. 56 (1991), pp. 673–683.Google Scholar
[2]Ash, C. J., Jockusch, C. G. Jr., and Knight, J. F., Jumps of orderings, Transactions of the American Mathematical Society, vol. 319 (1990), pp. 573–599.CrossRefGoogle Scholar
[3]Ash, C. J. and Knight, J., Computable structures and the hyperarithmetical hierarchy, Elsevier, Amsterdam, 2000.Google Scholar
[4]Ash, C. J., Knight, J., Manasse, M., and Slaman, T., Generic copies of countable structures, Annals of Pure and Applied Logic, vol. 42 (1989), pp. 195–205.CrossRefGoogle Scholar
[5]Badaev, S. A., Computable enumerations of families of general recursive functions, Algebra and Logic, vol. 16 (1977), pp. 129–148 (Russian), 83–98 (English translation).CrossRefGoogle Scholar
[6]Chisholm, J., Effective model theory vs. recursive model theory, this Journal, vol. 55 (1990), pp. 1168–1191.Google Scholar
[7]Gončarov, S. S., The number of nonautoequivalent constructivizations, Algebra and Logic, vol. 16 (1977), pp. 257–282 (Russian), 169–185 (English translation).Google Scholar
[8]Goncharov, S. S., Harizanov, V., Knight, J., McCoy, C., Miller, R., and Solomon, R., Enumerations in computable structure theory, Annals of Pure and Applied Logic, vol. 136 (2005), pp. 219–246.CrossRefGoogle Scholar
[9]Goncharov, S. S., Harizanov, V. S., Knight, J. F., and Shore, R. A., relations and paths through , this Journal, vol. 69 (2004), pp. 585–611.Google Scholar
[10]Manasse, M. S., Techniques and counterexamples in almost categorical recursive model theory, Ph.D. thesis, University of Wisconsin, Madison, 1982.Google Scholar
[11]Rogers, H. Jr., Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar
[12]Selivanov, V. L., The numerations of families of general recursive functions, Algebra and Logic, vol. 15 (1976), pp. 205–226 (Russian), 128–141 (English translation).CrossRefGoogle Scholar
[13]Soskov, I. N., Intrinsically hyperarithmetical sets, Mathematical Logic Quarterly, vol. 42 (1996), no. 4, pp. 469–480.CrossRefGoogle Scholar
[14]Watnick, R., A generalization of Tennenbaum's theorem on effectively finite recursive linear orderings, this Journal, vol. 49 (1984), pp. 563–569.Google Scholar