Published online by Cambridge University Press: 12 March 2014
A proof of the (propositional) Craig interpolation theorem for cut-free sequent calculus yields that a sequent with a cut-free proof (or with a proof with cut-formulas of restricted form; in particular, with only analytic cuts) with k inferences has an interpolant whose circuit-size is at most k. We give a new proof of the interpolation theorem based on a communication complexity approach which allows a similar estimate for a larger class of proofs. We derive from it several corollaries:
(1) Feasible interpolation theorems for the following proof systems:
(a) resolution
(b) a subsystem of LK corresponding to the bounded arithmetic theory 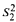 (α)
(α)
(c) linear equational calculus
(d) cutting planes.
(2) New proofs of the exponential lower bounds (for new formulas)
(a) for resolution ([15])
(b) for the cutting planes proof system with coefficients written in unary ([4]).
(3) An alternative proof of the independence result of [43] concerning the provability of circuit-size lower bounds in the bounded arithmetic theory 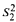 (α).
(α).
In the other direction we show that a depth 2 subsystem of LK does not admit feasible monotone interpolation theorem (the so called Lyndon theorem), and that a feasible monotone interpolation theorem for the depth 1 subsystem of LK would yield new exponential lower bounds for resolution proofs of the weak pigeonhole principle.