Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Matsubara, Yo
and
Usuba, Toshimichi
2021.
Advances in Mathematical Logic.
Vol. 369,
Issue. ,
p.
133.
Guzmán, Osvaldo
Hrušák, Michael
and
Zapletal, Jindřich
2021.
Preservation theorems for Namba forcing.
Annals of Pure and Applied Logic,
Vol. 172,
Issue. 2,
p.
102869.


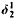 while preserving
while preserving 