Article contents
Functors and ordinal notations. I: A functorial construction of the veblen hierarchy
Published online by Cambridge University Press: 12 March 2014
Extract
This paper is the first of several works: the matter is the systematic rewriting of usual results of ordinal notations, using Π½-logic. The purpose of these articles is already realized in Π½-logic, in a relatively abstract form; also, they are examples for Π½-logic. The first and second articles in this series are complete versions of unpublished results that one of authors had announced in 1976.
Veblen introduced his hierarchy in 1908. The hierarchy has since been widely used in proof theory; in fact, what is actually needed is the more natural hierarchy: 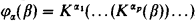 , with
, with 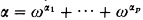 (not necessarily a Cantor normal form) and K the Veblen hierarchy.
(not necessarily a Cantor normal form) and K the Veblen hierarchy.
We shall show:
i) φ is in fact a two-variables functor (denoted by V in the text) commuting with direct limits and with pull-backs.
ii) The property of commutation with pull-backs permits one to give a representation of each ordinal x < φα(0) by means of a finite sequence of ordinals < α. This representation is independent of α it is ⊆ x, and can be used in the building up of notations systems. This representation is the “blowing-up” of the Cantor normal form, and it corresponds exactly to the denotation of ordinals < φα(0) by means of the functions (φβ)β<α.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1984
References
REFERENCES
- 9
- Cited by


