Article contents
Embedding jump upper semilattices into the Turing degrees
Published online by Cambridge University Press: 12 March 2014
Abstract
We prove that every countable jump upper semilattice can be embedded in 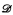 , where a jump upper semilattice (jusl) is an upper semilattice endowed with a strictly increasing and monotone unary operator that we call jump, and
, where a jump upper semilattice (jusl) is an upper semilattice endowed with a strictly increasing and monotone unary operator that we call jump, and 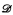 is the jusl of Turing degrees. As a corollary we get that the existential theory of 〈D, ≤T, ∨, ′〉 is decidable. We also prove that this result is not true about jusls with 0, by proving that not every quantifier free 1-type of jusl with 0 is realized in
is the jusl of Turing degrees. As a corollary we get that the existential theory of 〈D, ≤T, ∨, ′〉 is decidable. We also prove that this result is not true about jusls with 0, by proving that not every quantifier free 1-type of jusl with 0 is realized in 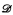 . On the other hand, we show that every quantifier free 1-type of jump partial ordering (jpo) with 0 is realized in
. On the other hand, we show that every quantifier free 1-type of jump partial ordering (jpo) with 0 is realized in 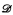 . Moreover, we show that if every quantifier free type, p(x1,…, xn), of jpo with 0, which contains the formula x1 ≤ 0(m) & … & xn ≤ 0(m) for some m, is realized in
. Moreover, we show that if every quantifier free type, p(x1,…, xn), of jpo with 0, which contains the formula x1 ≤ 0(m) & … & xn ≤ 0(m) for some m, is realized in 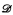 , then every quantifier free type of jpo with 0 is realized in
, then every quantifier free type of jpo with 0 is realized in 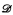 .
.
We also study the question of whether every jusl with the c.p.p. and size 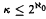 is embeddable in
is embeddable in 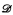 . We show that for
. We show that for 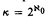 the answer is no, and that for κ = ℵ1 it is independent of ZFC. (It is true if MA(κ) holds.)
the answer is no, and that for κ = ℵ1 it is independent of ZFC. (It is true if MA(κ) holds.)
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2003
References
REFERENCES
- 3
- Cited by


