Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2025-01-03T17:28:54.295Z Has data issue: false hasContentIssue false
  • English
  • Français

A definability result for compact complex spaces

Published online by Cambridge University Press:  12 March 2014

Dale Radin
Dale Radin*
Affiliation:
Department of Mathematics, University of Illinois at Chicago, Chicago, IL, 60607, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A compact complex space X is viewed as a 1-st order structure by taking predicates for analytic subsets of X, X x X, … as basic relations. Let f: X → Y be a proper surjective holomorphic map between complex spaces and set Xy ≔ f−1(y). We show that the set

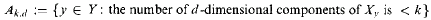
is analytically constructible, i.e.. is a definable set when X and Y are compact complex spaces and f: X → Y is a holomorphic map. The analogous result in the context of algebraic geometry gives rise to the definability of Morley degree.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 1 , March 2004 , pp. 241 - 254
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aroca, J. M., Hironaka, H., and Vicente, J. L., Desingularization theorems, Memorias de Matematica del Instituto “Jorge Juan”, no. 30, Madrid, 1977.Google Scholar
[2]Cartan, H., Détermination des points exceptionelles d'un système de p fonctions analytiques de n variables complexes, Bulletin des Sciences Mathématiques, II, Ser. 57. (1933), pp. 334–344.Google Scholar
[3]Fischer, G., Complex analytic geometry, Lecture Notes in Mathematics, vol. 538, Springer, 1976.CrossRefGoogle Scholar
[4]Frisch, J., Points de platitude d'un morphisme d'espaces analytiques complexes, Inventiones Mathematical, vol. 4 (1967), pp. 118–138.Google Scholar
[5]Grauert, H., Peternell, Th., and Remmert, R. (editors), Several complex variables VII, Encyclopaedia of Mathematical Sciences, vol. 74, Springer-Verlag, 1994.CrossRefGoogle Scholar
[6]Grauert, H. and Remmert, R., Coherent analytic sheaves, Grundlehren der mathematischen Wissenschaften, vol. 265, Springer-Verlag, 1984.Google Scholar
[7]Hrushovski, E., Strongly minimal expansions of algebraically closed fields, Israel Journal of Mathematics, vol. 79 (1992), pp. 129–151.Google Scholar
[8]Łojasibwicz, S., Introduction to complex analytic geometry, Birkhäuser-Verlag, 1991.CrossRefGoogle Scholar
[9]Moosa, R., Contributions to the model theory of fields and compact complex spaces, Ph.D. thesis, University of Illinois at Urbana-Champaign, 2001.Google Scholar
[10]Pillay, A. and Scanlon, T., Compact complex manifolds with the DOP and other properties, this Journal, vol. 67 (2002), pp. 737–743.Google Scholar
[11]Remmert, R., Holomorphe und meromorphe Abbildungen komplexer Räume, Mathematische Annalen, vol. 133 (1957), pp. 328–370.Google Scholar
[12]van den Dries, L., Model theory offields: decidability, and bounds for polynomial ideals, Ph.D. thesis, Universiteit Utrecht, 1978.Google Scholar
[13]Zilber, B., Model theory and algebraic geometry, Proceedings of the 10th Easter Conference on Model Theory (Berlin), 1993.Google Scholar