Article contents
The characteristic sequence of a first-order formula
Published online by Cambridge University Press: 12 March 2014
Abstract
For a first-order formula φ(x; y) we introduce and study the characteristic sequence (Pn: n < ω) of hypergraphs defined by 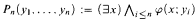 . We show that combinatorial and classification theoretic properties of the characteristic sequence reflect classification theoretic properties of φ and vice versa. The main results are a characterization of NIP and of simplicity in terms of persistence of configurations in the characteristic sequence. Specifically, we show that some tree properties are detected by the presence of certain combinatorial configurations in the characteristic sequence while other properties such as instability and the independence property manifest themselves in the persistence of complicated configurations under localization.
. We show that combinatorial and classification theoretic properties of the characteristic sequence reflect classification theoretic properties of φ and vice versa. The main results are a characterization of NIP and of simplicity in terms of persistence of configurations in the characteristic sequence. Specifically, we show that some tree properties are detected by the presence of certain combinatorial configurations in the characteristic sequence while other properties such as instability and the independence property manifest themselves in the persistence of complicated configurations under localization.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2010
References
REFERENCES
- 5
- Cited by


