Article contents
Chang's Conjecture and the Non-Stationary Ideal
Published online by Cambridge University Press: 12 March 2014
Extract
In The Axiom of Determinacy, Forcing Axioms and the Nonstationary Ideal [W1], Woodin constructs the partial order ℙmax, which in the presence of large cardinals yields a forcing extension of L(ℝ) where ZFC holds and the non-stationary ideal on ω1 (hereafter denoted NSω1) is ω2-saturated. The basic analysis of ℙmax forcing over L(ℝ) can be carried out assuming only the Axiom of Determinacy (AD). In the central result of this paper, we show that if one increases slightly the strength of the determinacy assumptions, then Chang's Conjecture—the assertion that every finitary algebra on ω2 has a subalgebra of order type ω1—holds in this extension as well. Specifically, we obtain:
Corollary 4.6. Assume AD + V = L(ℝ, μ) + μ is a normal, fine measure on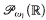 . Chang's Conjecture holds in any ℙmax-generic extension of L(ℝ).
. Chang's Conjecture holds in any ℙmax-generic extension of L(ℝ).
This technique for obtaining Chang's Conjecture is fairly general. We [Se] have adapted it to obtain Chang's Conjecture in the model presented by Steel and Van Wesep [SVW] and Woodin [Wl] has adapted it to his ℚmax forcing notion. In each of these models, as in the ℙmax extension, one forces over L(ℝ) assuming AD to obtain ZFC and NSω1 is ω2-saturated.
By unpublished results of Woodin, the assumption for Corollary 4.6 is equiconsistent with the existence of ω2 many Woodin cardinals, and hence strictly stronger than ADL(ℝ). One would like to reduce this assumption to ADL(ℝ). Curiously, this reduction is not possible in the arguments for ℚmax or the Steel and Van Wesep model, and the following argument of Woodin suggests why it may not be possible for ℙmax either.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2001
References
REFERENCES
- 2
- Cited by


