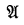Let and 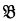be (well-formed) formulas of the functional calculus, let c be an n-adic functional variable, and let a1, …, an be distinct individual variables. Church has defined the metalogical notation 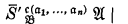to indicate the formula resulting from 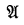when each part of 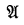of the form c{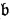1, …, 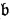n) (such that the occurrence of c is free in 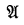) is replaced by the formula 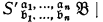which arises from 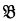by replacing every free occurrence of ai by 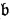i, i, = 1, …, n. (Here 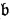1, …, 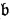n may be any individual variables or constants, not necessarily all distinct.) The notation is not defined for all 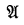, , 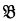c, a1, …, an, however, but only for those cases (specified in detail by Church) when the resulting formula constitutes a valid substitution instance of the formula 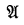according to the standard interpretation of the functional calculus.

The full and correct syntactical statement of the conditions (under which this type of substitution is permissible) has proved so arduous, that it seems to have been rendered in error more often than not. Unfortunately the functional calculi are often set up as deductive systems in which this type of substitution occurs as one of the primitive rules of inference, or in one of the axiom schemata. Thus the beginning student who is introduced to the calculi through such a formulation is forced to cope from the outset with details which have proved treacherous even to the initiate. For this reason it is desirable to seek alternative formulations of the functional calculi in which this type of substitution is not mentioned.