Article contents
Arithmetical problems and recursively enumerable predicates1
Published online by Cambridge University Press: 12 March 2014
Extract
It is an immediate consequence of results of Church and Gödel that there exist arithmetical recursively unsolvable problems, that is, recursively unsolvable problems of the form [M](P = Q) where P and Q are polynomials and [M] is some finite sequence of existential and universal quantifiers. A question which is immediately raised by this result is whether there exist unsolvable problems of this form where [M] is some finite sequence of existential quantifiers only. As a matter of fact this question is easily seen to be closely related to the tenth problem in the famous list proposed by Hilbert in 1900.
In this paper, we prove the existence of recursively unsolvable problems of the form
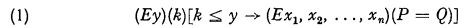
where P and Q are polynomials with non-negative integral coefficients. As a matter of fact we show that every recursively enumerable predicate is of the form (1), and conversely that every predicate of the form (1) is recursively enumerable. While our result does not yield the recursive unsolvability of Hilbert's tenth problem, it is easily seen that any considerable improvement of our result would yield this unsolvability.
The author wishes to take this opportunity to express his gratitude to Professors Alonzo Church and E. L. Post with whom he has had the privilege of discussing some of the questions involved in this paper. He also wishes to thank his friends Melvin Hausner and Jacob Schwartz who have made valuable suggestions.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1953
Footnotes
The results of this paper are included in [2], a thesis presented to the faculty of Princeton University in candidacy for the degree Doctor of Philosophy and accepted in May, 1950. The results were announced at a meeting of the Association for Symbolic Logic in December 1949 (cf. this Journal, vol. 15 (1950), p. 77).
References
REFERENCES
- 44
- Cited by


