Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-17T16:11:09.272Z Has data issue: false hasContentIssue false
  • English
  • Français

Arithmetical independence results using higher recursion theory

Published online by Cambridge University Press:  12 March 2014

Andrew Arana
Andrew Arana*
Affiliation:
Department of Philosophy, Building 90, Stanford University, Stanford, CA 94305-2155, USA, E-mail: [email protected], URL: http://www.stanford.edu/~aarana
Get access Rights & Permissions [Opens in a new window]

Abstract

We extend an independence result proved in [1]. We show that for all n, there is a special set of Πn sentences {φa}a ∈ H corresponding to elements of a linear ordering (H, <H) of order type 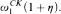. These sentences allow us to build completions {Ta}a ∈ H of PA such that for a <H b, Ta ∩ Σn ⊂ Tb ∩ Σn, with φa ∈ Ta, ¬φa ∈ Th. Our method uses the Barwise-Kreisel Compactness Theorem.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 1 , March 2004 , pp. 1 - 8
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Arana, Andrew, Solovay's theorem cannot be simplified, Annals of Pure and Applied Logic, vol. 112 (2001), no. 1, pp. 27–41.Google Scholar
[2]Ash, Christopher J. and Knight, Julia F., Computable structures and the hyperarithmetical hierarchy, Studies in Logic and the Foundations of Mathematics, vol. 144, Elsevier, Amsterdam, 2000.Google Scholar
[3]D'Aquino, Paola and Knight, Julia F., Coding in IΔ0, 2002, Preprint.Google Scholar
[4]Feferman, Solomon, Arithmetically definable models of formalizable arithmetic, Notices of the American Mathematical Society, vol. 5 (1958), p. 679.Google Scholar
[5]Kaye, Richard, Models of Peano Arithmetic, Oxford Logic Guides, vol. 15, Oxford University Press, Oxford, 1991.Google Scholar
[6]Rogers, Hartley, Theory of recursive functions and effective computability, MIT Press, Cambridge, 1967.Google Scholar
[7]Simmons, Harold, Large discrete parts of the E-tree, this Journal, vol. 53 (1988), no. 3, pp. 980–984.Google Scholar