Article contents
Arithmetic with creative definitions by induction
Published online by Cambridge University Press: 12 March 2014
Extract
The purpose of this paper is to present a system of arithmetic stronger than those usually employed, and to prove some syntactical theorems concerning it.
We presuppose the lower functional calculus with identity and functions, and we start with three of Peano's axioms.
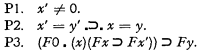
The other two (0 ϵ N and x ϵ N .⊃. x′ ϵ N) we do not need since our variables are anyhow restricted to natural numbers. Sometimes in the interest of a uniform notation for functions, we write Sx instead of x′.
Next we have two axioms for μ (the smallest number such that) as follows.
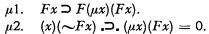
A third axiom for μ must wait until we have defined ≤.
Now we introduce the central feature of the system, the following rule of definition.
RD. Let Φ be a previously unused symbol. Then we can introduce it by a pair of definitions of the following form (n ≥ 0),
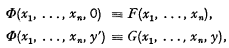
where F(x1, …, xn) is a wff in which no symbol occurs which was not previously defined (in particular, not Φ), and in which no free variables occur other than x1, …, xn (and possibly not all of these), and G(x1, …, xn, y) is a wff in which no free variables occur other than x1, …, xn, y (and possibly not all of these), and in which no symbol occurs which was not previously defined, except that Φ may occur but only if its last argument is y.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1953
References
1 Hilbert, and Bernays, , Grundlagen der Mathematik, vol. 2, Berlin, 1939, Supplement I B.Google Scholar
2 Loc. cit., vol. 1, Berlin, 1934, p. 371.
3 Loc. cit., vol. 2, p. 337.
4 Loc. cit., vol. 2, p. 338.
6 Lésniewski, S., Über definitionen in der sogenannten Theorie der Deduktion, Comptes rendus des stances de la Société des Sciences et des Lettres ds Varsovie, Classe III, vol. 24 (1931), pp. 289–309Google Scholar.
6 Loc. cit., vol. 2, p. 333.
7 (Added June 21, 1952.) Note that this proof requires α to be finite; if we could carry it out for arbitrary infinite α, we could obtain a contradiction by defining truth in K within K itself.
8 (Added January 14, 1952.) The consistency of RD relative to Gödel set theory follows from the fact that every definition permitted thereby is likewise permitted by an easy extension of 8.45 of Gödel's, The consistency of the axiom of choice and of the generalized continuum hypothesis with the axioms of set theory. Annals of Mathematics studies, no. 3, Princeton, 1940Google Scholar.
- 4
- Cited by


