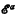 -arithmetic and transfinite induction
-arithmetic and transfinite inductionPublished online by Cambridge University Press: 12 March 2014
A hierarchy of systems of quantifier-free elementary recursive arithmetics, based on the Grzegorczyk hierarchy of functions, was set up in [2] and some meta-mathematical properties of these systems were developed. The Grzegorczyk hierarchy has been extended recently, mainly by Löb and Wainer [5], and our metamathematical developments may be similarly extended; the αth member of this hierarchy of formal systems will be denoted 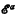 -arithmetic throughout. The main result in [2] was: For α > 1,
-arithmetic throughout. The main result in [2] was: For α > 1, 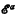 -arithmetic can be proved consistent in
-arithmetic can be proved consistent in 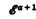 -arithmetic. In this paper we shall continue this work in particular, beginning with this consistency result, we shall find (for α > 1) the order type of the weakest simple transfinite induction scheme which is independent of
-arithmetic. In this paper we shall continue this work in particular, beginning with this consistency result, we shall find (for α > 1) the order type of the weakest simple transfinite induction scheme which is independent of 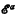 -arithmetic, thus giving a ‘measure of the complexity of derivations’ of these systems. For example we shall show that transfinite induction on a sequence of type ωω is a nonderivable rule of primitive recursive arithmetic (
-arithmetic, thus giving a ‘measure of the complexity of derivations’ of these systems. For example we shall show that transfinite induction on a sequence of type ωω is a nonderivable rule of primitive recursive arithmetic (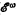 -arithmetic). This particular result was proved by Guard in [4] by a specialisation of a version of Gentzen's proof that ∈0-transfinite induction is independent of some standard formal systems of arithmetic with quantifiers. These methods can be adapted to our hierarchy but require what we might term an ‘ωω-jump’—that is if β is the largest ordinal for which transfinite induction up to β is derivable in the system in question then a scheme of transfinite induction up to β·ωω is independent. The proof presented in this paper requires only an ‘ω-jump’ and allows more precise results to be obtained for the systems in the extended Grzegorczyk hierarchy; it is also more direct and less proof-theoretic in character. We show that the consistency of
-arithmetic). This particular result was proved by Guard in [4] by a specialisation of a version of Gentzen's proof that ∈0-transfinite induction is independent of some standard formal systems of arithmetic with quantifiers. These methods can be adapted to our hierarchy but require what we might term an ‘ωω-jump’—that is if β is the largest ordinal for which transfinite induction up to β is derivable in the system in question then a scheme of transfinite induction up to β·ωω is independent. The proof presented in this paper requires only an ‘ω-jump’ and allows more precise results to be obtained for the systems in the extended Grzegorczyk hierarchy; it is also more direct and less proof-theoretic in character. We show that the consistency of 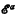 -arithmetic (for α > 1) can be proved in a system obtained by adding to
-arithmetic (for α > 1) can be proved in a system obtained by adding to 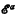 -arithmetic a transfinite induction scheme up to ω2, and that this induction scheme can be adapted to obtain the required result by increasing the ordinal and simultaneously decreasing the complexity of the functions involved in the induction scheme (detailed definitions of these concepts will be given in the next section).
-arithmetic a transfinite induction scheme up to ω2, and that this induction scheme can be adapted to obtain the required result by increasing the ordinal and simultaneously decreasing the complexity of the functions involved in the induction scheme (detailed definitions of these concepts will be given in the next section).