Article contents
Analytic cell decomposition and the closure of p-adic semianalytic sets
Published online by Cambridge University Press: 12 March 2014
Extract
The p-adic semianalytic sets are defined, locally, as boolean combinations of sets of the form 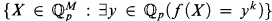 over the p-adic fields ℚp, where f is an analytic function. A well-know example due to Osgood showed the projection of a semianalytic set need not be a semianalytic set. We call those sets that are, locally, the projections of p-adic semianalytic sets p-adic subanalytic sets. The theory of p-adic subanalytic sets was presented by Denef and Van den Dries in [5]. The basic tools are the quantifier elimination techniques together with the ultrametric Weierstrass Preparation Theorem. Simultaneously with their developments of the p-adic subanalytic sets, they established some basic properties of p-adic semianalytic sets.
over the p-adic fields ℚp, where f is an analytic function. A well-know example due to Osgood showed the projection of a semianalytic set need not be a semianalytic set. We call those sets that are, locally, the projections of p-adic semianalytic sets p-adic subanalytic sets. The theory of p-adic subanalytic sets was presented by Denef and Van den Dries in [5]. The basic tools are the quantifier elimination techniques together with the ultrametric Weierstrass Preparation Theorem. Simultaneously with their developments of the p-adic subanalytic sets, they established some basic properties of p-adic semianalytic sets.
In this paper, we prove that the closure of any p-adic semianalytic set is also a semianalytic set. The analogous property for real semianalytic sets was proved in [12] and that for rigid semianalytic sets, informed by the referee, has been proved recently by a quite different method in [14] (cf. [9]). The keys to the proof are a separation lemma (Lemma 2) and an analytic cell decomposition theorem (Theorem 2) which is an analytic version of Denef's cell decomposition theorem (see [3, 4]; A total different form of anayltic cells appeared in [13]). The analytic cell decomposition theorem allows us to partition certain kinds of basic subsets into analytic cells that possess the closure property (see §1 for the definition).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1997
References
REFERENCES
- 1
- Cited by


