In this note we give a simple recursive axiomatization for the class of structures of type (ℶω ℵ0). This solves a problem of Vaught which is Problem 13 in the book [1] of Chang and Keisler. The same technique is used to get a recursive axiomatization for the class of κ-like structures where κ is strongly ω-inaccessible.

Let us fix throughout some recursive first-order language L, and until further notice let us suppose that included in L is a distinguished unary predicate symbol U. For cardinals κ and λ with κ ≥ λ ≥ ℵ0, we say the structure 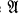has type (κ, λ) if card(A)= κ and card 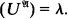. Let K(κ, λ) be the class of all structures of type (κ, λ). For each ordinal α define 2ακby 20κ = κ, and 2ακ= ⋃ {2λ: λ = 2βκ for some β < α} when α > 0. Let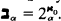

Vaught proved the following theorem in [7].

Theorem (Vaught). Suppose a is a sentence such that for each n < ω there are κ, λ with κ > 2λn and a model of σ of type (κ, λ). Then whenever κ ≥ λ ≥ ℵ0, the sentence σ has a model of type (κ, λ).