Ziegler studies in [2] the expressive power of (Lωω)t for T3 topological spaces. He defines for every natural number n the set 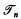of n-types by induction: 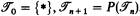. If A is a T3 space, the n-type of a ∈ A is defined inductively by: 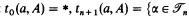: in every neighborhood of a there is an a′ ≠ a with tn(a′, A) = α}. These types are (Lωω)t-definable. Then, it is shown that two T3 spaces are (Lωω)t-equivalent precisely if for every n-type α they have the same number of points with n-type α (cf. [2]).

In order to study the expressability of (Lω1ω)t, for T3 spaces, we introduce in this paper the notion of accessible set. Looking at the behaviour of convergence by means of this notion, we refine Ziegler's notion of n-type and introduce a new set Sn of n-types, which are (Lω1ω)t-definable. Then, we prove a characterization of (Lω1ω)t-equivalence for a wide class of T3 spaces. A T3 space A belongs to this class if there is a κ ∈ ω such that, for every n ∈ ω, there are at most κ n-types in Sn which are satisfiable in A. Such a space is said to be of a-finite type. Some relations between these spaces and the spaces of finite type in the sense of [2] are shown in the last section.

The contents of the present paper are treated in more detail in [3].