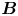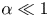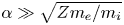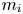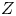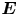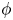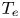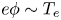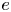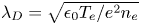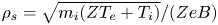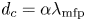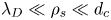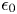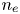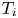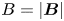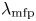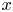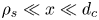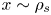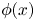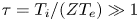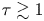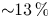A model is presented for the ion distribution function in a plasma at a solid target with a magnetic field 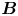 $\boldsymbol {B}$ inclined at a small angle,
$\boldsymbol {B}$ inclined at a small angle, 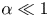 $\alpha \ll 1$ (in radians), to the target. Adiabatic electrons are assumed, requiring
$\alpha \ll 1$ (in radians), to the target. Adiabatic electrons are assumed, requiring 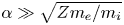 $\alpha \gg \sqrt {Zm_{e}/m_{i}}$, where
$\alpha \gg \sqrt {Zm_{e}/m_{i}}$, where 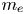 $m_{e}$ and
$m_{e}$ and 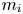 $m_{i}$ are the electron and ion mass, respectively, and
$m_{i}$ are the electron and ion mass, respectively, and 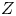 $Z$ is the charge state of the ion. An electric field
$Z$ is the charge state of the ion. An electric field 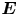 $\boldsymbol {E}$ is present to repel electrons, and so the characteristic size of the electrostatic potential
$\boldsymbol {E}$ is present to repel electrons, and so the characteristic size of the electrostatic potential 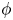 $\phi$ is set by the electron temperature
$\phi$ is set by the electron temperature 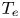 $T_{e}$,
$T_{e}$, 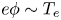 $e\phi \sim T_{e}$, where
$e\phi \sim T_{e}$, where 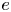 $e$ is the proton charge. An asymptotic scale separation between the Debye length
$e$ is the proton charge. An asymptotic scale separation between the Debye length 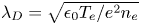 $\lambda _{D} = \sqrt {\epsilon _0 T_{{e}} / e^{2} n_{{e}} }$, the ion sound gyro-radius
$\lambda _{D} = \sqrt {\epsilon _0 T_{{e}} / e^{2} n_{{e}} }$, the ion sound gyro-radius 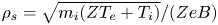 $\rho _{s} = \sqrt { m_{i} ( ZT_{e} + T_{i} ) } / (ZeB)$ and the size of the collisional region
$\rho _{s} = \sqrt { m_{i} ( ZT_{e} + T_{i} ) } / (ZeB)$ and the size of the collisional region 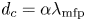 $d_{c} = \alpha \lambda _{\textrm {mfp}}$ is assumed,
$d_{c} = \alpha \lambda _{\textrm {mfp}}$ is assumed, 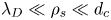 $\lambda _{D} \ll \rho _{s} \ll d_{c}$. Here
$\lambda _{D} \ll \rho _{s} \ll d_{c}$. Here 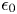 $\epsilon _0$ is the permittivity of free space,
$\epsilon _0$ is the permittivity of free space, 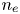 $n_{e}$ is the electron density,
$n_{e}$ is the electron density, 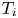 $T_{i}$ is the ion temperature,
$T_{i}$ is the ion temperature, 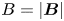 $B= |\boldsymbol {B}|$ and
$B= |\boldsymbol {B}|$ and 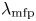 $\lambda _{\textrm {mfp}}$ is the collisional mean free path of an ion. The form of the ion distribution function is assumed at distances
$\lambda _{\textrm {mfp}}$ is the collisional mean free path of an ion. The form of the ion distribution function is assumed at distances 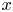 $x$ from the wall such that
$x$ from the wall such that 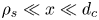 $\rho _{s} \ll x \ll d_{c}$, that is, collisions are not treated. A self-consistent solution of the electrostatic potential for
$\rho _{s} \ll x \ll d_{c}$, that is, collisions are not treated. A self-consistent solution of the electrostatic potential for 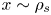 $x \sim \rho _{s}$ is required to solve for the quasi-periodic ion trajectories and for the ion distribution function at the target. The large gyro-orbit model presented here allows to bypass the numerical solution of
$x \sim \rho _{s}$ is required to solve for the quasi-periodic ion trajectories and for the ion distribution function at the target. The large gyro-orbit model presented here allows to bypass the numerical solution of 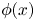 $\phi (x)$ and results in an analytical expression for the ion distribution function at the target. It assumes that
$\phi (x)$ and results in an analytical expression for the ion distribution function at the target. It assumes that 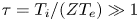 $\tau =T_{i}/(ZT_{e})\gg 1$, and ignores the electric force on the quasi-periodic ion trajectory until close to the target. For
$\tau =T_{i}/(ZT_{e})\gg 1$, and ignores the electric force on the quasi-periodic ion trajectory until close to the target. For 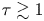 $\tau \gtrsim 1$, the model provides an extremely fast approximation to energy–angle distributions of ions at the target. These can be used to make sputtering predictions.
$\tau \gtrsim 1$, the model provides an extremely fast approximation to energy–angle distributions of ions at the target. These can be used to make sputtering predictions.