The Vlasov equation is solved by a phase-space boundary integration method in order to investigate the nonlinear frequency of an electron plasma mode. Unlike the familiar discrete particle simulation codes in which a limited number of particles may be considered, the present model represents a more realistic plasma case in which a very large number (practically unlimited) of plasma particles evolving in their self-consistent collective field is investigated. The unperturbed collisionless one-dimensional plasma system consists of warm electrons having a water-bag distribution to simulate equilibrium, and of static ions. The initial perturbation is introduced by changing the boundaries of the electron plasma such that υu = υ0 (1 + α.sin kx) and υl = − υ0(1 − α sin kx), υu and υl representing the upper and the lower boundaries, respectively. This corresponds to a standing wave perturbation. The results obtained for different wavelength perturbations λ ≡ 2π/k, and for several perturbation amplitudes α, are presented and discussed.

The paper contains an analysis of the linearized plasma-dynamical equations, including the energy conservation equations, and accounting completely for all the dissipative mechanisms, in the absence of external fields. The eigenvalues of the 14 plasmadynamical modes are obtained systematically in terms of the transport coefficients of the plasma.

The kinetic theory of a plasma is developed on the basis of a normal mode analysis-In the absence of any external field, the system approaches a ‘plasmadynamical (PD) state’, described by fourteen amplitudes of the PD modes. The corresponding eigenvalues and eigenvectors are constructed explicitly. When an external time-dependent electric field is switched on, transitions between these modes determine the evolution of the plasma. Assuming that a PD regime is valid, the kinetic equations reduce to a set of equations describing parametric effects and nonlinear mode-mode couplings. A new source term, arising from the interference between collisions and external field, also appears. Some qualitative implications are discussed.

The Fokker-Planck equation is studied for an energetic ion beam injected into a magnetized plasma consisting of Maxwellian ions and electrons with υthi ≪υb≪ υthe. The time evolution of the fast ion distribution is given in terms of an infinite sum of Legendre polynomials for distributions that are axisymmetric about the magnetic field. The effect of charge exchange is included. The resulting ion distribution is somewhat isotropic for velocities much less than the injection velocity, however, the distribution is sharply peaked in both energy and pitch angle for velocities near the injection velocity. Approximate asymptotic expressions are given for the distribution in the vicinity of the injected beam and for velocities greater than the injection velocity. The effect of a weak parallel electric field is also given.

There is considerable interest in the use of energetic ion beams to heat magnetically confined plasmas to ignition temperature. An uncertainty in this heating technique is the possible role of instabilities driven by the fast ion beams. For this reason, we have investigated homogeneous plasma modes, including the cross field ion-ion wave and the beam ion-acoustic wave, as well as the ordinary electromagnetic mode, which taps the free energy associated with the beam anisotropy. The growth rates of these modes are calculated and the stability thresholds are compared to parameters for both present injection experiments and the proposed TFTR device.

Incompressible turbulent flows are investigated in the framework of ideal magnetohydrodynamics. All the field quantities vary with only two spatial dimensions. Equilibrium canonical distributions are determined in a phase space whose co-ordinates are the real and imaginary parts of the Fourier coefficients for the field variables. In the geometry considered, the magnetic field and fluid velocity have variable x and y components, and all field quantities are independent of z. Three constants of the motion are found (one of them new) which survive the truncation in Fourier space and permit the construction of canonical distributions with three independent temperatures. Spectral densities are calculated. One of the more novel physical effects is the appearance of macroscopic structures involving long wavelength, self-generated, magnetic fields (‘magnetic islands’) for a wide range of initial parameters. Current filaments show a tendency toward consolidation in much the same way that vorticity filaments do in the guiding-centre plasma case. In the presence of finite dissipation, energy cascades to higher wavenumbers can be accompanied by vector potential cascades to lower wavenumbers, in much the same way as, in the fluid dynamic (Navier-Stokes) case, energy cascades to lower wavenumbers accompany enstrophy cascades to higher wavenumbers. It is suggested that the techniques may be relevant to theories of the magnetic dynamo problem and to the generation of megagauss magnetic fields when pellets are irradiated by lasers.

A general formalism for describing two-time fluctuations in magnetized plasma is presented. Two-time expectations of one-body operators (phase functions) are written in terms of the phase space density autocorrelation function

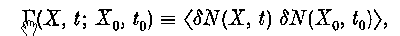
where δN is the fluctuation in the singular Klimontovich microdensity. It is shown that 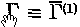is the first member of a set of two-time quantities

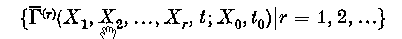
which collectively obeys the linearized BBGKY cumulant hierarchy in the (Xi, t) variables, with initial conditions successively smaller in the plasma parameter 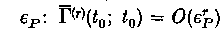. We study in detail the case of fluctuations in thermal equilibrium, although the general formalism holds also for the non-equilibrium case. To lowest order in εP, Γ obeys the linearized Vlasov equation. From this are recovered all of Rostoker's results for fluctuations excited by Cherenkov emission and absorbed by Landau damping, as well as a constructive proof of the test particle superposition principle. To first order, Γ obeys (in the Markovian approximation) the linearized Balescu-Guernsey-Lenard equation. For frequencies and wavenumbers in the hydrodynamic regime, the velocity moments of Γ obey linearized fluid equations with classical transport coefficients (i.e. essentially those computed by Braginskii in the 3-D case). It has been found that the classical theory is in disagreement with certain computer and laboratory experiments performed in strong magnetic fields. This defect is attributed to the absence in the classical theory of contributions to the collision operator, hence transport coefficients, of fluctuations long-lived on the Vlasov scale. Analogous difficulties arise in the theory of hydrodynamics in neutral fluids. To improve the plasma theory, a renormalization of the two-time hierarchy is proposed which sums selected terms from all orders in εP and thus treats the hydrodynamic fluctuations self-consistently. The resulting theory retains appropriate fluid conservation laws, thereby avoiding erroneous results encountered in certain diffusing orbit theories, when the fluid viscosity is indiscriminantly replaced by the test particle diffusion coefficient. In order to explain the results of the computer simulations, the theory is applied in part 2 to the problem of anomalous hydrodynamic contributions to the transport coefficients.

The general formalism for treating two-time fluctuations in magnetized plasma, developed in part 1 of this series, is applied to the case of anomalous cross-field transport in 2-D, strongly magnetized, thermal equilibrium systems. For (where εP is the plasma parameter), classical predictions for the ion shear viscosity and test particle diffusion coefficients are dominated by the anomalous contributions of low frequency, long wavelength hydrodynamic fluctuations (convective cells). The anomalous transport is discussed from the points of view of (a) kinetic theory; (b) the assumption of long-time local thermal equilibrium (Landau-Placzek method); and (c) a renormalized mode-coupling version of the generalized Langevin equation. The results of all these approaches are in agreement, and they predict that the transport coefficients scale with magnetic field B as 1/B for, and as independent of B for

in good agreement with the computer simulations of Okuda & Dawson. The transport is weakly non-Markovian, the Green-Kubo integrands decay non-classically for long times as [t ln (t)]−½, and the test particle ‘;diffusion’ coefficient does not asymptotically approach a constant for t → ∞.