The Kelvin–Helmholtz instability, proposed a long time ago for its role in and impact on the transport properties at magnetospheric flanks, has been widely investigated in the Earth’s magnetosphere context. This review covers more than fifty years of theoretical and numerical efforts in investigating the evolution of Kelvin–Helmholtz vortices and how the rich nonlinear dynamics they drive allow solar wind plasma bubbles to enter into the magnetosphere. Special care is devoted to pointing out the main advantages and weak points of the different plasma models that can be adopted for describing the collisionless magnetospheric medium and in underlying the important role of the three-dimensional geometry of the system.

We investigate the question of how plasma currents circulate and close in the scrape-off-layer (SOL) of convection-limited tokamak plasmas. A simplified two-fluid model describes how currents must evacuate charge at the sheaths due to cross-field currents that are not divergence-free. These include turbulence-driven polarization currents and poloidally asymmetric equilibrium diamagnetic currents. The theory provides an estimate for the radial profile of the floating potential, which reveals a dipolar structure like the one observed experimentally. Simulations with a fluid turbulence code provide evidence for the predicted behaviour of currents and floating potential.

The extreme properties of the gamma-ray flares in the Crab nebula present a clear challenge to our ideas on the nature of particle acceleration in relativistic astrophysical plasma. It seems highly unlikely that standard mechanisms of stochastic type are at work here and hence the attention of theorists has switched to linear acceleration in magnetic reconnection events. In this series of papers, we attempt to develop a theory of explosive magnetic reconnection in highly magnetized relativistic plasma which can explain the extreme parameters of the Crab flares. In the first paper, we focus on the properties of the X-point collapse. Using analytical and numerical methods (fluid and particle-in-cell simulations) we extend Syrovatsky’s classical model of such collapse to the relativistic regime. We find that the collapse can lead to the reconnection rate approaching the speed of light on macroscopic scales. During the collapse, the plasma particles are accelerated by charge-starved electric fields, which can reach (and even exceed) values of the local magnetic field. The explosive stage of reconnection produces non-thermal power-law tails with slopes that depend on the average magnetization $\unicode[STIX]{x1D70E}$. For sufficiently high magnetizations and vanishing guide field, the non-thermal particle spectrum consists of two components: a low-energy population with soft spectrum that dominates the number census; and a high-energy population with hard spectrum that possesses all the properties needed to explain the Crab flares.

Using analytical and numerical methods (fluid and particle-in-cell simulations) we study a number of model problems involving merger of magnetic flux tubes in relativistic magnetically dominated plasma. Mergers of current-carrying flux tubes (exemplified by the two-dimensional ‘ABC’ structures) and zero-total-current magnetic flux tubes are considered. In all cases regimes of spontaneous and driven evolution are investigated. We identify two stages of particle acceleration during flux mergers: (i) fast explosive prompt X-point collapse and (ii) ensuing island merger. The fastest acceleration occurs during the initial catastrophic X-point collapse, with the reconnection electric field of the order of the magnetic field. During the X-point collapse, particles are accelerated by charge-starved electric fields, which can reach (and even exceed) values of the local magnetic field. The explosive stage of reconnection produces non-thermal power-law tails with slopes that depend on the average magnetization $\unicode[STIX]{x1D70E}$. For plasma magnetization $\unicode[STIX]{x1D70E}\leqslant 10^{2}$ the spectrum power-law index is $p>2$; in this case the maximal energy depends linearly on the size of the reconnecting islands. For higher magnetization, $\unicode[STIX]{x1D70E}\geqslant 10^{2}$, the spectra are hard, $p<2$, yet the maximal energy $\unicode[STIX]{x1D6FE}_{\text{max}}$ can still exceed the average magnetic energy per particle, ${\sim}\unicode[STIX]{x1D70E}$, by orders of magnitude (if $p$ is not too close to unity). The X-point collapse stage is followed by magnetic island merger that dissipates a large fraction of the initial magnetic energy in a regime of forced magnetic reconnection, further accelerating the particles, but proceeds at a slower reconnection rate.

A numerical investigation is carried out to understand the equilibrium 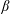$\unicode[STIX]{x1D6FD}$-limit in a classical stellarator. The stepped-pressure equilibrium code (Hudson et al., Phys. Plasmas, vol. 19 (11), 2012) is used in order to assess whether or not magnetic islands and stochastic field-lines can emerge at high 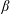$\unicode[STIX]{x1D6FD}$. Two modes of operation are considered: a zero-net-current stellarator and a fixed-iota stellarator. Despite the fact that relaxation is allowed (Taylor, Rev. Mod. Phys., vol. 58 (3), 1986, pp. 741–763), the former is shown to maintain good flux surfaces up to the equilibrium 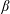$\unicode[STIX]{x1D6FD}$-limit predicted by ideal-magnetohydrodynamics (MHD), above which a separatrix forms. The latter, which has no ideal equilibrium 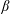$\unicode[STIX]{x1D6FD}$-limit, is shown to develop regions of magnetic islands and chaos at sufficiently high 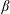$\unicode[STIX]{x1D6FD}$, thereby providing a ‘non-ideal 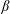$\unicode[STIX]{x1D6FD}$-limit’. Perhaps surprisingly, however, the value of 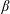$\unicode[STIX]{x1D6FD}$ at which the Shafranov shift of the axis reaches a fraction of the minor radius follows in all cases the scaling laws predicted by ideal-MHD. We compare our results to the High-Beta-Stellarator theory of Freidberg (Ideal MHD, 2014, Cambridge University Press) and derive a new prediction for the non-ideal equilibrium 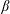$\unicode[STIX]{x1D6FD}$-limit above which chaos emerges.

The properties of a non-relativistic magnetised low-beta electron–positron plasma in slab geometry are investigated. The two species are taken to be drift kinetic while we retain Larmor radius effects in quasi-neutrality, and inertia in Ohm’s law. A linear analysis shows that, for small magnetic perturbations, Alfvénic perturbations travel at the electron Alfvén speed, which is based on the electron mass. We discuss the role of the displacement current when Larmor-scale and Debye-scale effects are both retained. We predict the existence of a kinetic electron Alfvén wave which connects to the K-modes of Mishchenko et al. (J. Plasma Phys., 2017 (submitted)) in the electrostatic limit. It is found that linear drift waves are not supported by the system if the two species have the same temperature. Tearing modes can be driven unstable by equilibrium current density gradients. Also in this case, the characteristic time is based on the electron Alfvén speed. Nonlinear hybrid fluid-kinetic equations are also derived. It is shown that each species is described, to leading order, by the kinetic reduced electron heating model (KREHM) kinetic equation of Zocco & Schekochihin (Phys. Plasmas, vol. 18, 2011, 102309). The model is extended to retain first-order Larmor radius effects. It supports collisionless dispersive waves, which can greatly impact nonlinear magnetic reconnection. Diamagnetic effects enter the nonlinear equations via the first-order magnetic compressibility. A minimal nonlinear model for two-dimensional low-frequency isothermal pair plasmas is derived.

The time evolution of slow sound waves in a homogeneous, collisionless and quasineutral plasma, in particular their Landau damping, is investigated using the kinetic-magnetohydrodynamics formulation of Ramos (J. Plasma Phys. vol. 81, 2015 p. 905810325; vol. 82, 2016 p. 905820607). In this approach, the electric field is eliminated from a closed, hybrid fluid-kinetic system that ensures automatically the fulfilment of the charge neutrality condition. Considering the time dependence of a spatial-Fourier-mode linear perturbation with wavevector parallel to the equilibrium magnetic field, this can be cast as a second-order self-adjoint problem with a continuum spectrum of real and positive squared frequencies. Therefore, a conventional resolution of the identity with a continuum basis of singular normal modes is guaranteed, which simplifies significantly a Van Kampen-like treatment of the Landau damping. The explicit form of such singular normal modes is obtained, along with their orthogonality relations. These are used to derive the damped time evolution of the fluid moments of solutions of initial-value problems, for the most general kinds of initial conditions. The non-zero parallel electric field is not used explicitly in this analysis, but it is calculated from any given solution after the later has been obtained.

The nonlinear dynamics of energetic-particle (EP) driven geodesic acoustic modes (EGAM) is investigated here. A numerical analysis with the global gyrokinetic particle-in-cell code ORB5 is performed, and the results are interpreted with the analytical theory, in close comparison with the theory of the beam-plasma instability. Only axisymmetric modes are considered, with a nonlinear dynamics determined by wave–particle interaction. Quadratic scalings of the saturated electric field with respect to the linear growth rate are found for the case of interest. As a main result, the formula for the saturation level is provided. Near the saturation, we observe a transition from adiabatic to non-adiabatic dynamics, i.e. the frequency chirping rate becomes comparable to the resonant EP bounce frequency. The numerical analysis is performed here with electrostatic simulations with circular flux surfaces, and kinetic effects of the electrons are neglected.

Nanopulse atmospheric carbon monoxide discharges and corresponding afterglows have been investigated in a wide range of applied reduced electric field (130 < E/N < 200 Td) and different pulse durations (2–50 ns). The results have been obtained by solving an appropriate Boltzmann equation for the electron energy distribution function (EEDF) coupled to the kinetics of vibrational and electronic excited states as well as to a simplified plasma chemistry for the different species formed during the activation of CO. The molar fraction of electronically excited states generated in the discharge is sufficient to create structures in the EEDF in the afterglow regime. On the other hand, only for long duration pulses (i.e. 50 ns), non-equilibrium vibrational distributions can be observed especially in the afterglow. The trend of the results for the case study E/N = 200 Td, $\unicode[STIX]{x1D70F}_{\text{pulse}}=2$  ns is qualitatively and quantitatively similar to the corresponding case for CO2 implying that the activation of CO2 by cold plasmas should take into account the kinetics of formed CO with the same accuracy as the CO2 itself.

The influence of finite Larmor radius correction, tensor viscosity and uniform rotation on self-gravitational and firehose instabilities is discussed in the framework of the quantum magnetohydrodynamic and Chew–Goldberger–Low (CGL) fluid models. The general dispersion relation is obtained for transverse and longitudinal modes of propagation. In both the modes of propagation the dispersion relation is further analysed with respect to the direction of the rotational axis. In the analytical discussion the axis of rotation is considered in parallel and in the perpendicular direction to the magnetic field. (i) In the transverse mode of propagation, when rotation is parallel to the direction of the magnetic field, the Jeans instability criterion is affected by the rotation, finite Larmor radius (FLR) and quantum parameter but remains unaffected due to the presence of tensor viscosity. The calculated critical Jeans masses for rotating and non-rotating dense degenerate plasma systems are $3.5M_{\odot }$ and $2.1M_{\odot }$ respectively. It is clear that the presence of rotation enhances the threshold mass of the considered system. (ii) In the case of longitudinal mode of propagation when rotation is parallel to the direction of the magnetic field, Alfvén and viscous self-gravitating modes are obtained. The Alfvén mode is modified by FLR corrections and rotation. The analytical as well as graphical results show that the presence of FLR and rotation play significant roles in stabilizing the growth rate of the firehose instability by suppressing the parallel anisotropic pressure. The viscous self-gravitating mode is significantly affected by tensor viscosity, anisotropic pressure and the quantum parameter while it remains free from rotation and FLR corrections. When the direction of rotation is perpendicular to the magnetic field, the rotation of the considered system coupled the Alfvén and viscous self-gravitating modes to each other. The finding of the present work is applicable to strongly magnetized dense degenerate plasma.

Magnetic reconnection is a fundamental energy conversion mechanism in nature. Major attempts to study this process in controlled settings on Earth have largely been limited to reproducing approximately two-dimensional (2-D) reconnection dynamics. Other experiments describing reconnection near three-dimensional null points are non-driven, and do not induce any of the 3-D modes of spine fan, torsional fan or torsional spine reconnection. In order to study these important 3-D modes observed in astrophysical plasmas (e.g. the solar atmosphere), laboratory set-ups must be designed to induce driven reconnection about an isolated magnetic null point. As such, we consider the limited range of fundamental resistive magnetohydrodynamic (MHD) and kinetic parameters of dynamic laboratory plasmas that are necessary to induce the torsional spine reconnection (TSR) mode characterized by a driven rotational slippage of field lines – a feature that has yet to be achieved in operational laboratory magnetic reconnection experiments. Leveraging existing reconnection models, we show that within a ${\lesssim}1~\text{m}^{3}$ apparatus, TSR can be achieved in dense plasma regimes (${\sim}10^{24}~\text{m}^{-3}$) in magnetic fields of ${\sim}10^{-1}~\text{T}$. We find that MHD and kinetic parameters predict reconnection in thin ${\lesssim}20~\unicode[STIX]{x03BC}\text{m}$ current sheets on time scales of ${\lesssim}10~\text{ns}$. While these plasma regimes may not explicitly replicate the plasma parameters of observed astrophysical phenomena, studying the dynamics of the TSR mode within achievable set-ups signifies an important step in understanding the fundamentals of driven 3-D magnetic reconnection and the self-organization of current sheets. Explicit control of this reconnection mode may have implications for understanding particle acceleration in astrophysical environments, and may even have practical applications to fields such as spacecraft propulsion.

The Fokker–Planck transport equation describing the motion of energetic particles through a plasma is explored analytically. The latter equation provides a pitch-angle and position-dependent distribution function of the charged particles. In the current paper the first 14 moments of this equation are computed exactly for an arbitrary initial pitch angle. Such analytical forms are required in nonlinear treatments of perpendicular transport and other scenarios in plasma physics and astrophysics.

We present a series of experiments on novel, line-tied plasma geometries as a study of the generation of chaos and turbulence in line-tied systems. Plasma production and the injection scale for magnetic energy is provided by spatially discrete plasma guns that inject both plasma and current. The guns represent a technique for controlling the injection scale of magnetic energy. A two-dimensional (2-D) array of magnetic probes provides spatially resolved time histories of the magnetic fluctuations at a single cross-section of the experimental cylinder, allowing simultaneous spatial measurements of chaotic and turbulent behaviour. The first experiment shows chaotic fluctuations and self-organization in a hollow-current line-tied screw pinch. These dynamics is modulated primarily by the applied magnetic field and weakly by the plasma current and safety factor. The second experiment analyses the interactions of multiple line-tied flux ropes. The flux ropes all exhibit chaotic behaviour, and under certain conditions develop an inverse cascade to larger scales and a turbulent inertial range with magnetic energy ($E$) related to perpendicular wave number ($k_{\bot }$) as $E\propto k_{\bot }^{-2.5\pm 0.5}$.

In this paper, we consider the asymptotic behaviour of solitons and double layers. By using the Sagdeev pseudopotential formalism, a Taylor series expansion is used to derive the asymptotic behaviour. For solitons and supersolitons that propagate faster than the acoustic speed, an exponential decay rate is derived. In contrast, for acoustic speed solitons and supersolitons, we show that the decay rate is algebraic, resulting in much fatter tails. These results can be extended to double layers. However, the double layer velocity affects only one side of the tail. The other side of the tail is affected by the multiplicity of the double layer root. All the results are illustrated by means of a case study.

A drift-kinetic model to describe the plasma dynamics in the scrape-off layer region of tokamak devices at arbitrary collisionality is derived. Our formulation is based on a gyroaveraged Lagrangian description of the charged particle motion, and the corresponding drift-kinetic Boltzmann equation that includes a full Coulomb collision operator. Using a Hermite–Laguerre velocity space decomposition of the gyroaveraged distribution function, a set of equations to evolve the coefficients of the expansion is presented. By evaluating explicitly the moments of the Coulomb collision operator, distribution functions arbitrarily far from equilibrium can be studied at arbitrary collisionalities. A fluid closure in the high-collisionality limit is presented, and the corresponding fluid equations are compared with previously derived fluid models.

The self-similar expansion of an adiabatic electronegative dusty plasma (consisting of inertialess adiabatic electrons, inertialess adiabatic ions and inertial adiabatic negatively charged dust fluids) is theoretically investigated by employing the self-similar approach. It is found that the effects of the plasma adiabaticity (represented by the adiabatic index $\unicode[STIX]{x1D6FE}$) and dusty plasma parameters (determined by dust temperature and initial dust population) significantly modify the nature of the plasma expansion. The implications of our results are expected to play an important role in understanding the physics of the expansion of space and laboratory electronegative dusty plasmas.

A set of layer equations for determining the stability of semi-collisional tearing modes in an axisymmetric torus, incorporating neoclassical physics, in the small ion Larmor radius limit, is provided. These can be used as an inner layer module for inclusion in numerical codes that asymptotically match the layer to toroidal calculations of the tearing mode stability index, $\unicode[STIX]{x1D6E5}^{\prime }$. They are more complete than in earlier work and comprise equations for the perturbed electron density and temperature, the ion temperature, Ampère’s law and the vorticity equation, amounting to a twelvth-order set of radial differential equations. While the toroidal geometry is kept quite general when treating the classical and Pfirsch–Schlüter transport, parallel bootstrap current and semi-collisional physics, it is assumed that the fraction of trapped particles is small for the banana regime contribution. This is to justify the use of a model collision term when acting on the localised (in velocity space) solutions that remain after the Spitzer solutions have been exploited to account for the bulk of the passing distributions. In this respect, unlike standard neoclassical transport theory, the calculation involves the second Spitzer solution connected with a parallel temperature gradient, because this stability problem involves parallel temperature gradients that cannot occur in equilibrium toroidal transport theory. Furthermore, a calculation of the linearised neoclassical radial transport of toroidal momentum for general geometry is required to complete the vorticity equation. The solutions of the resulting set of equations do not match properly to the ideal magnetohydrodynamic (MHD) equations at large distances from the layer, and a further, intermediate layer involving ion corrections to the electrical conductivity and ion parallel thermal transport is invoked to achieve this matching and allow one to correctly calculate the layer $\unicode[STIX]{x1D6E5}^{\prime }$.

We calculate the disruption scale $\unicode[STIX]{x1D706}_{\text{D}}$ at which sheet-like structures in dynamically aligned Alfvénic turbulence are destroyed by the onset of magnetic reconnection in a low-$\unicode[STIX]{x1D6FD}$ collisionless plasma. The scaling of $\unicode[STIX]{x1D706}_{\text{D}}$ depends on the order of the statistics being considered, with more intense structures being disrupted at larger scales. The disruption scale for the structures that dominate the energy spectrum is $\unicode[STIX]{x1D706}_{\text{D}}\sim L_{\bot }^{1/9}(d_{e}\unicode[STIX]{x1D70C}_{s})^{4/9}$, where $d_{e}$ is the electron inertial scale, $\unicode[STIX]{x1D70C}_{s}$ is the ion sound scale and $L_{\bot }$ is the outer scale of the turbulence. When $\unicode[STIX]{x1D6FD}_{e}$ and $\unicode[STIX]{x1D70C}_{s}/L_{\bot }$ are sufficiently small, the scale $\unicode[STIX]{x1D706}_{\text{D}}$ is larger than $\unicode[STIX]{x1D70C}_{s}$ and there is a break in the energy spectrum at $\unicode[STIX]{x1D706}_{\text{D}}$, rather than at $\unicode[STIX]{x1D70C}_{s}$. We propose that the fluctuations produced by the disruption are circularised flux ropes, which may have already been observed in the solar wind. We predict the relationship between the amplitude and radius of these structures and quantify the importance of the disruption process to the cascade in terms of the filling fraction of undisrupted structures and the fractional reduction of the energy contained in them at the ion sound scale $\unicode[STIX]{x1D70C}_{s}$. Both of these fractions depend strongly on $\unicode[STIX]{x1D6FD}_{e}$, with the disrupted structures becoming more important at lower $\unicode[STIX]{x1D6FD}_{e}$. Finally, we predict that the energy spectrum between $\unicode[STIX]{x1D706}_{\text{D}}$ and $\unicode[STIX]{x1D70C}_{s}$ is steeper than $k_{\bot }^{-3}$, when this range exists. Such a steep ‘transition range’ is sometimes observed in short intervals of solar-wind turbulence. The onset of collisionless magnetic reconnection may therefore significantly affect the nature of plasma turbulence around the ion gyroscale.

Analytical models for nonlinear electron plasma waves in weakly magnetized plasmas are developed for single as well as multi-mode conditions, with continuous wave spectra being a limiting case. The conditions for wave decay as well as modulational instabilities are analysed. Our results demonstrate that slow or nearly stationary plasma density variations can be found for weakly magnetized plasmas even for weakly nonlinear electron plasma waves without involving cavitation of large amplitude plasma waves. A reduction of the growth rates for decay as well as modulational instabilities are found when the spectral width of the wave spectrum is increased. Some of our results are relevant for the interpretation of the nonlinearly enhanced ion acoustic lines often observed in non-equilibrium ionospheres.

The interaction of radio frequency waves with charged particles in a magnetized plasma is usually described by the quasilinear operator that was originally formulated by Kennel & Engelmann (Phys. Fluids, vol. 9, 1966, pp. 2377–2388). In their formulation the plasma is assumed to be homogenous and embedded in a uniform magnetic field. In tokamak plasmas the Kennel–Engelmann operator does not capture the magnetic drifts of the particles that are inherent to the non-uniform magnetic field. To overcome this deficiency a combined drift and gyrokinetic derivation is employed to derive the quasilinear operator for radio frequency heating and current drive in a tokamak with magnetic drifts retained. The derivation requires retaining the magnetic moment to higher order in both the unperturbed and perturbed kinetic equations. The formal prescription for determining the perturbed distribution function then follows a novel procedure in which two non-resonant terms must be evaluated explicitly. The systematic analysis leads to a diffusion equation that is compact and completely expressed in terms of the drift kinetic variables. The equation is not transit averaged, and satisfies the entropy principle, while retaining the full poloidal angle variation without resorting to Fourier decomposition. As the diffusion equation is in physical variables, it can be implemented in any computational code. In the Kennel–Engelmann formalism, the wave–particle resonant delta function is either for the Landau resonance or the Doppler shifted cyclotron resonance. In the combined gyro and drift kinetic approach, a term related to the magnetic drift modifies the resonance condition.