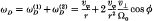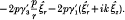Research Article
Ion-acoustic double layers
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 353-360
Alfvén surface waves in a two-ion-species cylindrical plasma with finite edge density
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 361-378
Modulational instability of obliquely modulated ion-acoustic waves in a collisional plasma with one- and two-electron-temperature distributions
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 379-394
Ion-acoustic double layers in multi-species plasmas maintained by negative ions
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 395-406
The equilibrium of sheared, rippled, magnetically focused beams of relativistic charged particles
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 407-420
Higher-order approximations for the growth rate of the Weibel instability in strongly anisotropic plasmas
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 421-428
Transition scattering of waves on charged dust particles in a plasma
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 429-443
Dispersion properties of dusty plasmas
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 445-456
Transient nonlinear wave mixing in collisional plasmas
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 457-478
Linear and nonlinear geometric optics. Part 1. Constitutive relations and three-wave interaction
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 479-493
Linear and nonlinear geometric optics. Part 2. The Vlasov-Maxwell equations
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 495-506
Nonlinear modulational stability and propagation of an electromagnetic pulse in a two-component neutral plasma
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 507-519
Influence of an ambient magnetic field on the nonlinear modulational stability of circularly polarized electromagnetic pulses in a two-component neutral plasma
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 521-530
Corrigendum
Corrigendum
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 531-532
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Book Review
The Theory of Target Compression by Longwave Laser Emission, edited by G. V. Slizkov. Nova Science Publishers, NY. pp. 167. $73.
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 533-534
Author Index to Volume 42
Index
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 535-537
Front matter
PLA volume 42 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Back matter
PLA volume 42 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. b1-b10
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service

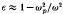 for the unperturbed case (cold plasma), we find that
for the unperturbed case (cold plasma), we find that 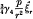
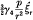
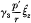
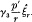
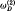 in
in