Second-order perturbation calculation shows that an explosive instability of three resonantly interacting coherent electrostatic waves can be limited, and converted into a multiple-periodic process by nonlinear terms of the same order as those that destabilize the waves in the first-order approximation. No higher- order nonlinearities are necessary. The method used is purely classical, and consists in transforming the Hamiltonian of the waves into angle-action variables, and canonical averaging of the Hamiltonian over the proper angles. The number of degrees of freedom is thus reduced to one, which permits one to analyse the wave interaction in the phase plane without using the usual equations for the complex wave amplitudes.

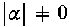We formulate, in the framework of MHD, a simple eigenvalue problem, capable of treating the stability of force-free magnetic fields curl B = αB in different geometries. We prove that a force-free field surrounded by a rigid wall is stable, if the eigenvalue α corresponds to the lowest value of compatible with the geometry considered. We extend this result to the case where α is a function of position; and we recliscuss it from the viewpoint of the first-order variation. We give various theorems and criteria for stability, for continuous as well as for admissible discontinuous or infinite displacements. A general upper limit for the growth rate is 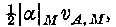, where and 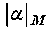and are respectively the maximum values of 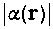and υAthe Alfvén velocity inthe plasma volume.

Theorems and criteria on stability of force-free fields, developed in part 1 (Krüger 1976) are illustrated for continuous, as well as discontinuous, spectra of α. Previous and new results are understood from a unified viewpoint.

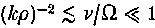The paper investigates the effect, on the Bernstein-mode dispersion relation, of a small collision frequency v, such that , for the high-frequency regime. It is shown that the ion-acoustic mode dominates the Bernstein modes in this regime for homogeneous plasmas; and it is suggested that this also holds for inhomogeneous plasmas.

By using the concept of combined field, we present a simple and symmetric Hamiltonian formulation for an infinitely conducting fluid, moving in an electromagnetic field. The definition of the combined field potentials makes it possible to replace the interaction between the electromagnetic field and charges by an interaction between two fields. Some applications are made, to prove the theory (e.g. the Hamiltonian of a point charge, Fourier representation).

Sturrock's theory of stochastic acceleration and Dupree's theory of strong plasma turbulence are here derived in a very simple way, showing that trapping cannot correctly be taken into account by this kind of theory. A comparison of Sturrock and Dupree's diffusion coefficients D shows that they differ significantly only in the domain where these theories fail, and where the highest values of D are reached. The need for a theory taking trapped orbits into account appears clearly. Such an attempt is the object of a sequel.

The recurrence of ion waves has been examined experimentally in the region where the nonlinearity is so weak that recurrence length is determined oniy by dispersion. We observe that the recurrence length is longer than the theoretical prediction derived from the Korteweg–de Vries equation of hot ions, and that the recurrence is imperfect. The result is qualitatively explained by wave–particle interaction.

This paper studies the linear dispersion properties of ion temperature anisotropy instabilities in an infinite, homogeneous Vlasov plasma containing a second, cooler-ion component. The cooler component enhances the T‖>T⊥ firehose instability, as well as the T⊥>T‖, ion-cyclotron instability, by making the waves more resonant with the ions. The effect of various parameters on this enhancement is studied numerically.

The problem of harmonic and subharmonic generation of electrostatic waves in a general collisionless plasma, or in some other electromagnetic medium, is treated anew, using coupled-mode theory based on two time scales. A novel feature is that one of the two interacting waves may be a negative energy wave. Furthermore, the model describing the medium need not be specified, only a general linear and nonlinear conductivity or an equivalent description is required. Just by invoking wave energy conservation, the coupled-mode equations are obtained in such a way that unequivocal conclusions can be drawn.

When both waves have positive energy, they exchange part of it in a periodic fashion, provided they both have some energy initially. If initially all the energy is in the fundamental, then all of it will eventually end up (irreversibly) in thesecond harmonic. If, on the other hand, all the energy is in the harmonic initially, then no generation of the fundamental (or subharmonic) will take place. If one of the two waves is a negative-energy wave, however, an explosive instability develops, and this regardless of initial values. For comparable conditions, the instability time depends on whether the negative energy wave is in the fundamental or in the upper harmonic.

The paper investigates the stability of electrostatic waves in non-uniform magnetoplasmas, governed by anti-loss-cone distributions. A new high- frequency anti-loss-cone instability occurs if ρ > ρc. (ρ is the parameter charactensing the strength of the anti-loss-cone.) An increase in ρ increases the growth rates for this instability, but stabilizes the low-frequency instability that exists even in the absence of the anti-loss cone. The growth rates can be of order 0.1Ωe.

In propagation perpendicular to the magnetic field, the lower hybrid frequency is the transition between long electromagnetic and short electrostatic waves. Cold, warm and hot plasma theories are applied to the case of a plasma composed of different ion species. For cold and warm (adiabatic) theories, the dispersion curves are not qualitatively different from the single-ion case. In the hot microscopic theory, the dispersion curves, the so-called ‘Bernstein modes’, have a structure mainly related to the lightest ion gyroharmonics, even in concentration as low as 1 %. The theoretical results can explain the ray structure observed in the ISIS II and Electron Echo 1 experiments.

The Green's function (or matrix) for a source of sinusoidal time dependence in an infinite homogeneous absorbing magneto-ionic plasma is written as a Fourier integral over wavenumber space. It is shown that this Fourier integral solution exists, and is unique as a generalized function. By extending the Fourier integral to complex wavenumbers, it is shown that the far-field expression for the Green's function may be written as an integral over sections of the dispersion surface, which in this case is a complex sub-manifold of the space of three complex variables. Use of the saddle-point method in two dimensions allows a further simplification of the far-field result. The matrix coefficients in the resulting expression are shown to represent a decomposition into modes. Corresponding results are also obtained for sources with spatial dependence, described by either functions of compact support or rapidly decreasing functions.

A ray or quasi-optical approximation is developed, using complex rays. The ‘amplitude’ terms are matrices, rather than vectors that represent the wave polarization. Thus, the way the propagation resolves a source into various modes is described. The second term in the amplitude series is shown to include a type of inter-mode coupling. It is shown that initial values needed to integrate along the rays can be chosen so that the leading term of the approximation agrees with the far-field solution for localized sources in a homogeneous medium. By invoking the ‘canonical problem’ method, the result is extended to give an approximation for the Green's matrix in a slowly-varying medium.

For the purpose of deriving appropriate Lagrangians for equations in plasma physics that include effects of energy loss, the paper examines the inverse problem of the calculus of variations for systems of first and second order quasi- linear partial differential equations. This results in convenient forms of the sufficient conditions, under which the given differential equations are Euler Lagrange equations of a Lagrangian. These conditions are then applied, to determine the necessary transformation that converts equations, apparently not already in it, into Euler—Lagrange form. The appropriate Lagrangian for a warm collisional plasma is obtained. As an additional example, the Lagrangian is derived for a resistive transmission line.