Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-27T05:27:20.453Z Has data issue: false hasContentIssue false
  • English
  • Français

General stability analysis of force-free magnetic fields. Part 1. General theory

Published online by Cambridge University Press:  13 March 2009

Jan Krüger
Jan Krüger
Affiliation:
Seminarie voor Wiskundige Natuurkunde, Rijksuniversiteit Ghent, Krijgslaan 271, S9, B-9000 Ghent, Belgium
Get access Rights & Permissions [Opens in a new window]

Abstract

We formulate, in the framework of MHD, a simple eigenvalue problem, capable of treating the stability of force-free magnetic fields curl B = αB in different geometries. We prove that a force-free field surrounded by a rigid wall is stable, if the eigenvalue α corresponds to the lowest value of 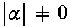compatible with the geometry considered. We extend this result to the case where α is a function of position; and we recliscuss it from the viewpoint of the first-order variation. We give various theorems and criteria for stability, for continuous as well as for admissible discontinuous or infinite displacements. A general upper limit for the growth rate is 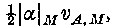, where and 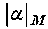and are respectively the maximum values of 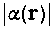and υAthe Alfvén velocity inthe plasma volume.

Type
Research Article
Information
Journal of Plasma Physics , Volume 15 , Issue 1 , February 1976 , pp. 15 - 30
Copyright
Copyright © Cambridge University Press 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bernstein, I. B., Frieman, E. A., Kruskal, M. D., & Kulsrud, R. M. 1958 Proc. Roy. Soc. A 244, 17.Google Scholar
Chandrasekhar, S., & Woltjer, L. 1958 Proc. Nat. Acad. Sci. 44, 285.CrossRefGoogle Scholar
Goedbloed, J. P. 1970 Phys. Rev. Lett. 24, 253.CrossRefGoogle Scholar
Jette, A. D. 1970 J. Math. An. Appl. 29, 109.CrossRefGoogle Scholar
Krüger, J. 1967 Verh. Kon. Vl. Ac. Wet. België, 19, 97.Google Scholar
Krüger, J. G., & Callebaut, D. K. 1967 Mém. Soc. Roy. Sci. Liège 5me Sér. 15, 175.Google Scholar
Krüger, J. G., & Callebaut, D. K. 1972 Proc. 5th European, Conf. on Controlled Fusion and Plasma Phys. Grenoble, 31.Google Scholar
Krüger, J. 1976 J. Plasma Phys. 15, 31.CrossRefGoogle Scholar
Lundquist, S. 1951 Phys. Rev. 83, 307.CrossRefGoogle Scholar
Newcomb, W. A. 1959 Phys. Fluids, 2, 362.CrossRefGoogle Scholar
Richter, E. 1960 Z. Phys. 159, 194.CrossRefGoogle Scholar
Schäfer, P. 1970 Beitr. Piasmaphys. 10, 21.CrossRefGoogle Scholar
Schmidt, G. 1966 Physics of High-Temperature Plasmas. Academic.Google Scholar
Voslamber, D., & Callebaut, D. K. 1962 Phys. Rev. 128, 2016.CrossRefGoogle Scholar
Wagner, R. 1971 Z. Naturforsch. A 26, 1753.CrossRefGoogle Scholar
Woltjer, L. 1958 Proc. Nat. Acad. Sci. 44, 489.CrossRefGoogle Scholar
Woltjer, L. 1959 Proc. Nat. Acad. Sci. 45, 769.CrossRefGoogle Scholar