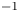1. Introduction
Ion stopping in plasma is an important topic in inertial confinement fusion (ICF) which is researched as a potential source of energy. The energy loss of the 3.5 MeV $\alpha$![]() -particles produced in deuterium–tritium fusion reactions must dominate all loss processes, causing the target to self-heat, ultimately leading to further fusion reactions. Therefore, modelling the various plasmas within the dynamic environments of a burning fusion pellet is necessary. This is especially true for ignition and the launch of a thermonuclear burn wave, which will ultimately result in an energy gain (Hurricane et al. Reference Hurricane2016). For target heating schemes using ion beams as the primary drivers, such as heavy-ion fusion (Callahan-Miller & Tabak Reference Callahan-Miller and Tabak2000) or ion-driven fast ignition (Fernandez et al. Reference Fernandez, Albright, Beg, Foord, Hegelich, Honrubia, Roth, Stephens and Yin2014), ion stopping in a plasma is also essential. Theoretical treatment of ion stopping remains a challenging problem despite decades of extensive analytical and numerical studies. The Born approximation and other perturbative theories (Maynard & Deutsch Reference Maynard and Deutsch1985; Peter & Meyer-Ter-Vehn Reference Peter and Meyer-Ter-Vehn1991; Li & Petrasso Reference Li and Petrasso1993; Deutsch et al. Reference Deutsch2010) are in good agreement with the data when the projectile ion velocity is much higher than the thermal velocity of the plasma electrons ($v_{i}\gg v_{e,\text {th}}$
-particles produced in deuterium–tritium fusion reactions must dominate all loss processes, causing the target to self-heat, ultimately leading to further fusion reactions. Therefore, modelling the various plasmas within the dynamic environments of a burning fusion pellet is necessary. This is especially true for ignition and the launch of a thermonuclear burn wave, which will ultimately result in an energy gain (Hurricane et al. Reference Hurricane2016). For target heating schemes using ion beams as the primary drivers, such as heavy-ion fusion (Callahan-Miller & Tabak Reference Callahan-Miller and Tabak2000) or ion-driven fast ignition (Fernandez et al. Reference Fernandez, Albright, Beg, Foord, Hegelich, Honrubia, Roth, Stephens and Yin2014), ion stopping in a plasma is also essential. Theoretical treatment of ion stopping remains a challenging problem despite decades of extensive analytical and numerical studies. The Born approximation and other perturbative theories (Maynard & Deutsch Reference Maynard and Deutsch1985; Peter & Meyer-Ter-Vehn Reference Peter and Meyer-Ter-Vehn1991; Li & Petrasso Reference Li and Petrasso1993; Deutsch et al. Reference Deutsch2010) are in good agreement with the data when the projectile ion velocity is much higher than the thermal velocity of the plasma electrons ($v_{i}\gg v_{e,\text {th}}$![]() ) (Dietrich et al. Reference Dietrich, Hoffmann, Wahl, Haas, Kunze, Brandenburg and Noll1990; Hoffmann et al. Reference Hoffmann, Weyrich, Wahl, Gardés, Bimbot and Fleurier1990; Roth et al. Reference Roth, Stöckl, Süss, Iwase, Gericke, Bock, Hoffmann, Geissel and Seelig2000; Frank et al. Reference Frank2013; Zylstra et al. Reference Zylstra2015). The ion stopping at $v_{i}\le v_{e,\text {th}}$
) (Dietrich et al. Reference Dietrich, Hoffmann, Wahl, Haas, Kunze, Brandenburg and Noll1990; Hoffmann et al. Reference Hoffmann, Weyrich, Wahl, Gardés, Bimbot and Fleurier1990; Roth et al. Reference Roth, Stöckl, Süss, Iwase, Gericke, Bock, Hoffmann, Geissel and Seelig2000; Frank et al. Reference Frank2013; Zylstra et al. Reference Zylstra2015). The ion stopping at $v_{i}\le v_{e,\text {th}}$![]() is more difficult to describe, but is typically explained by collisional theories that take into account two-body collisions and large-angle scattering between the ions and the plasma electrons. Due to the strong scattering at ion velocities close to $v_{e,\text {th}}$
is more difficult to describe, but is typically explained by collisional theories that take into account two-body collisions and large-angle scattering between the ions and the plasma electrons. Due to the strong scattering at ion velocities close to $v_{e,\text {th}}$![]() and significant collective effects, the Born approximation becomes unreliable, and collisional theories fail to provide a thorough, self-consistent understanding of ion stopping. This is attributed to the dynamic dielectric response of the plasma electrons. This coincides with the regime in which the stopping power is at its maximum. Compared with the conventional perturbative models, stopping theories that thoroughly account for coupling effects between projectiles and plasma electrons predict energy losses of 30–50 % less (Gericke & Schlanges Reference Gericke and Schlanges1999, Reference Gericke and Schlanges2003; Brown, Preston & Singleton Reference Brown, Preston and Singleton2005; Cayzac et al. Reference Cayzac2015). In ICF, these theoretical uncertainties hinder the precise prediction of $\alpha$
and significant collective effects, the Born approximation becomes unreliable, and collisional theories fail to provide a thorough, self-consistent understanding of ion stopping. This is attributed to the dynamic dielectric response of the plasma electrons. This coincides with the regime in which the stopping power is at its maximum. Compared with the conventional perturbative models, stopping theories that thoroughly account for coupling effects between projectiles and plasma electrons predict energy losses of 30–50 % less (Gericke & Schlanges Reference Gericke and Schlanges1999, Reference Gericke and Schlanges2003; Brown, Preston & Singleton Reference Brown, Preston and Singleton2005; Cayzac et al. Reference Cayzac2015). In ICF, these theoretical uncertainties hinder the precise prediction of $\alpha$![]() -particle heating, since the condition $v_\alpha \le v_{e,\text {th}}$
-particle heating, since the condition $v_\alpha \le v_{e,\text {th}}$![]() holds for the majority of the time range. In fact, a decreased $\alpha$
holds for the majority of the time range. In fact, a decreased $\alpha$![]() -particle stopping causes a nearly equal increase in range. This may have an impact on the thermonuclear burn wave's ignition threshold in the dense main fuel as well as the energy deposition inside the hot spot of a burning deuterium–tritium plasma (Edie et al. Reference Edie, Vorberger, Rose and Gericke2013). By leveraging the advantages of the various approaches used in the various regimes, rigorous quantum mechanical treatments based on convergent kinetic theories attempt to address these issues (Frieman & Book Reference Frieman and Book1963; Kihara et al. Reference Kihara, Aono, Kihara and Aono1963; Gould & DeWitt Reference Gould and DeWitt1967; Brown et al. Reference Brown, Preston and Singleton2005); however, it is unclear how to combine them and quantify their errors. Therefore, accurate measurements of the ion stopping near the stopping maximum are crucial for directing theoretical efforts. Although many attempts have been made to theoretically describe the behaviour of ion stopping in high energy density (HED) plasmas (Maynard & Deutsch Reference Maynard and Deutsch1985; Zimmerman Reference Zimmerman1997; Peter & Meyer-Ter-Vehn Reference Peter and Meyer-Ter-Vehn1991; Li & Petrasso Reference Li and Petrasso1993; Gericke & Schlanges Reference Gericke and Schlanges1999; Brown et al. Reference Brown, Preston and Singleton2005; Deutsch et al. Reference Deutsch2010), there is only a small body of experimental evidence to support these theories (Cayzac et al. Reference Cayzac2017; Chen et al. Reference Chen2018; Frenje et al. Reference Frenje2019; Hayes et al. Reference Hayes2020; Zylstra et al. Reference Zylstra, Rygg, Collins, Li, Frenje, Petrasso, Nagel, Fitzsimmons and Reynolds2020; Malko et al. Reference Malko2021). This is because suitable laser-generated plasmas in these measurements are typically very small and highly transient, leading to great demands on the equipment of the experimental area and, in particular, on the plasma probing ion beam.
-particle stopping causes a nearly equal increase in range. This may have an impact on the thermonuclear burn wave's ignition threshold in the dense main fuel as well as the energy deposition inside the hot spot of a burning deuterium–tritium plasma (Edie et al. Reference Edie, Vorberger, Rose and Gericke2013). By leveraging the advantages of the various approaches used in the various regimes, rigorous quantum mechanical treatments based on convergent kinetic theories attempt to address these issues (Frieman & Book Reference Frieman and Book1963; Kihara et al. Reference Kihara, Aono, Kihara and Aono1963; Gould & DeWitt Reference Gould and DeWitt1967; Brown et al. Reference Brown, Preston and Singleton2005); however, it is unclear how to combine them and quantify their errors. Therefore, accurate measurements of the ion stopping near the stopping maximum are crucial for directing theoretical efforts. Although many attempts have been made to theoretically describe the behaviour of ion stopping in high energy density (HED) plasmas (Maynard & Deutsch Reference Maynard and Deutsch1985; Zimmerman Reference Zimmerman1997; Peter & Meyer-Ter-Vehn Reference Peter and Meyer-Ter-Vehn1991; Li & Petrasso Reference Li and Petrasso1993; Gericke & Schlanges Reference Gericke and Schlanges1999; Brown et al. Reference Brown, Preston and Singleton2005; Deutsch et al. Reference Deutsch2010), there is only a small body of experimental evidence to support these theories (Cayzac et al. Reference Cayzac2017; Chen et al. Reference Chen2018; Frenje et al. Reference Frenje2019; Hayes et al. Reference Hayes2020; Zylstra et al. Reference Zylstra, Rygg, Collins, Li, Frenje, Petrasso, Nagel, Fitzsimmons and Reynolds2020; Malko et al. Reference Malko2021). This is because suitable laser-generated plasmas in these measurements are typically very small and highly transient, leading to great demands on the equipment of the experimental area and, in particular, on the plasma probing ion beam.
The majority of the experiments mentioned used conventional particle accelerators, similar to that carried out by Cayzac et al. (Reference Cayzac2017) (see figure 1). In this particular experiment, nitrogen ions were accelerated using the UNIversal Linear ACcelerator (UNILAC) situated at GSI. The ions had an energy of 0.6 MeV u$^{-1}$![]() and were delivered in bunches lasting $\tau =5.5$
and were delivered in bunches lasting $\tau =5.5$![]() ns (FWHM) with approximately 1000 ions per bunch. These accelerated ions probed a carbon plasma characterised by free electron densities of up to $n_{e}=10^{20}\ {\rm cm}^{-3}$
ns (FWHM) with approximately 1000 ions per bunch. These accelerated ions probed a carbon plasma characterised by free electron densities of up to $n_{e}=10^{20}\ {\rm cm}^{-3}$![]() and a maximum temperature of $T_\text {max}= 150$
and a maximum temperature of $T_\text {max}= 150$![]() eV. Two nanosecond lasers, called Petawatt High Energy Laser for Ion eXperiments (PHELIX) and Nanosecond High Energy Laser for Ion eXperiments (nhelix), generated the plasma. Although the experiment was considered highly successful, the obtained results exhibited significant temporal uncertainties. This can be attributed to the 5.5 ns ion bunch length used in the experiment. As the plasma expands on the nanosecond time scale, its parameters undergo rapid changes, as illustrated in figure 2, displaying simulated temperature profiles at various times during the expansion. Consequently, within the probing ion bunch, leading ions encounter different plasma conditions than trailing ions, causing temporal uncertainties. This issue can be reduced by implementing shorter ion bunches, which can be achieved through the use of laser-generated ions as they have a lower longitudinal emittance (Cowan et al. Reference Cowan2004). Another important advantage is the three to four orders of magnitude increase in the number of ions within a probing bunch, resulting in a higher signal-to-noise ratio. This enables an improved measurement accuracy of the stopping power.
eV. Two nanosecond lasers, called Petawatt High Energy Laser for Ion eXperiments (PHELIX) and Nanosecond High Energy Laser for Ion eXperiments (nhelix), generated the plasma. Although the experiment was considered highly successful, the obtained results exhibited significant temporal uncertainties. This can be attributed to the 5.5 ns ion bunch length used in the experiment. As the plasma expands on the nanosecond time scale, its parameters undergo rapid changes, as illustrated in figure 2, displaying simulated temperature profiles at various times during the expansion. Consequently, within the probing ion bunch, leading ions encounter different plasma conditions than trailing ions, causing temporal uncertainties. This issue can be reduced by implementing shorter ion bunches, which can be achieved through the use of laser-generated ions as they have a lower longitudinal emittance (Cowan et al. Reference Cowan2004). Another important advantage is the three to four orders of magnitude increase in the number of ions within a probing bunch, resulting in a higher signal-to-noise ratio. This enables an improved measurement accuracy of the stopping power.

Figure 1. Schematic illustration of the previous stopping power experiment conducted by Cayzac et al. (Reference Cayzac2017).

Figure 2. Two-dimensional hydrodynamic simulations (MULTI2D Ramis, Meyer-ter Vehn & Ramírez Reference Ramis, Meyer-ter Vehn and Ramírez2009) along the laser axis ($z$![]() ): a carbon foil with a areal density of $100\ \mathrm {\mu }{\rm g}\ {\rm cm}^{-2}$
): a carbon foil with a areal density of $100\ \mathrm {\mu }{\rm g}\ {\rm cm}^{-2}$![]() is irradiated by two lasers beams from both sides (right side of the expansion is shown) with a pulse length of 7 ns (FWHM), a wavelength of 526.5 nm, a focal spot size of 1 mm (supergauss) and an energy of 30 J. (a) Simulated plasma temperature at different times of the expansion. (b) Simulated free electron density in the plasma at different times of the expansion.
is irradiated by two lasers beams from both sides (right side of the expansion is shown) with a pulse length of 7 ns (FWHM), a wavelength of 526.5 nm, a focal spot size of 1 mm (supergauss) and an energy of 30 J. (a) Simulated plasma temperature at different times of the expansion. (b) Simulated free electron density in the plasma at different times of the expansion.
Therefore, we intend to expand this experimental dataset by using ions generated by a laser-driven beamline as a probe beam, which have favourable properties compared with ions accelerated by traditional linear accelerators. Intense multi-MeV ion bunches with brief durations can be produced on a $\mathrm {\mu }$![]() m-scale by laser plasma accelerators. As a result, the characteristics of these laser-generated beams are fundamentally different from those of traditional ion sources, potentially broadening the range of the accelerators’ potential for use in research and applications. They can deliver ions with energies above 100 MeV (Kim et al. Reference Kim2016; Wagner et al. Reference Wagner2016; Higginson et al. Reference Higginson2018; Ziegler et al. Reference Ziegler, Assenbaum, Brack, Cowan, Dover, Kluge, Kraft and Kroll2023), in picoseconds at the source (Dromey et al. Reference Dromey2016). The target normal sheath acceleration (TNSA) (Wilks et al. Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely2001), which is particularly suitable due to its robustness and the ensuing reliability, is the most researched and frequently used laser-driven ion acceleration mechanism. The initial TNSA beam is not suitable for the majority of the aforementioned applications due to its broad energy spread, large divergence, and the presence of background radiation in the form of electromagnetic pulses (EMP), X-rays and electrons close to its origin. Using the advantages of laser-driven ions, Malko et al. (Reference Malko2021) conducted a successful stopping power experiment with laser-generated protons using magnetic filtering for the energy selection. In numerous laboratories all over the world, a different approach is used to shape the beam to the specific requirements which is the combination of laser-driven beamlines with conventional accelerator components like quadrupoles, solenoids and plasma lenses (Brack et al. Reference Brack2020; Rösch et al. Reference Rösch2020; Zhu et al. Reference Zhu2020; Apiñaniz et al. Reference Apiñaniz2021; Kroll et al. Reference Kroll2022).
m-scale by laser plasma accelerators. As a result, the characteristics of these laser-generated beams are fundamentally different from those of traditional ion sources, potentially broadening the range of the accelerators’ potential for use in research and applications. They can deliver ions with energies above 100 MeV (Kim et al. Reference Kim2016; Wagner et al. Reference Wagner2016; Higginson et al. Reference Higginson2018; Ziegler et al. Reference Ziegler, Assenbaum, Brack, Cowan, Dover, Kluge, Kraft and Kroll2023), in picoseconds at the source (Dromey et al. Reference Dromey2016). The target normal sheath acceleration (TNSA) (Wilks et al. Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely2001), which is particularly suitable due to its robustness and the ensuing reliability, is the most researched and frequently used laser-driven ion acceleration mechanism. The initial TNSA beam is not suitable for the majority of the aforementioned applications due to its broad energy spread, large divergence, and the presence of background radiation in the form of electromagnetic pulses (EMP), X-rays and electrons close to its origin. Using the advantages of laser-driven ions, Malko et al. (Reference Malko2021) conducted a successful stopping power experiment with laser-generated protons using magnetic filtering for the energy selection. In numerous laboratories all over the world, a different approach is used to shape the beam to the specific requirements which is the combination of laser-driven beamlines with conventional accelerator components like quadrupoles, solenoids and plasma lenses (Brack et al. Reference Brack2020; Rösch et al. Reference Rösch2020; Zhu et al. Reference Zhu2020; Apiñaniz et al. Reference Apiñaniz2021; Kroll et al. Reference Kroll2022).
In this context, the Laser Ion Generation, Handling and Transport (LIGHT) collaboration (Busold et al. Reference Busold2014a) was established, and a laser-driven beamline was constructed at GSI. The primary objective of the LIGHT collaboration is to explore the feasibility of working with laser-driven ion beams using traditional accelerator components. Using this understanding, the collaboration aims to maximise bunch intensity and demonstrate the potential of laser-driven beamlines. Due to the preexisting infrastructure at GSI, it is possible to run a radio-frequency (rf) cavity, giving the LIGHT beamline the ability to manipulate the bunches longitudinally and thereby lessen their energy spread or even compress them temporally (Ikegami et al. Reference Ikegami2009; Busold et al. Reference Busold2013, Reference Busold, Schumacher, Deppert, Brabetz, Kroll, BlaŽević, Bagnoud and Roth2014b, Reference Busold2015; Teng et al. Reference Teng, Gu, Zhu, Hong, Zhao, Zhou and Cao2013; Jahn et al. Reference Jahn2019; Metternich et al. Reference Metternich2022). The expertise of the Helmholtz-Zentrum Dresden-Rossendorf (HZDR) regarding pulsed high-field solenoid magnets is also advantageous to the LIGHT collaboration. These solenoids have optimised the LIGHT beamline's transverse focusing and capture efficiency.
In this article, we report on the planned stopping power experiment with the LIGHT beamline and the results of two preparatory experimental campaigns in which we demonstrated the generation of the required ion beams and performed a stopping power experiment in a cold foil.
2. Planned stopping power experiment
In this section, the planned stopping power experiment with the LIGHT beamline will be presented.
The experiment will be performed in the experimental area Z6 at GSI. The set-up of the planned experiment is depicted in figure 3. The objective is to use laser-generated ions with the shortest possible bunch length to investigate their stopping power in a laser-generated plasma. The probed plasma will have a maximum temperature of 150 eV. To achieve the highest ion–plasma coupling in the stopping maximum regime, it is essential to match the velocity of the probing ions with the thermal plasma electrons. This necessitates an energy per mass ratio of 0.5 MeV u$^{-1}$![]() for the ions. This is a much lower energy per mass than usually targeted at the LIGHT beamline, especially for protons.
for the ions. This is a much lower energy per mass than usually targeted at the LIGHT beamline, especially for protons.

Figure 3. Schematic illustration of the planned stopping power experiment with the LIGHT beamline at the Z6 experimental area of GSI.
The ions are generated and accelerated within the Z6 target chamber via the TNSA mechanism using the PHELIX laser (Bagnoud et al. Reference Bagnoud2010). At the Z6 experimental area, the PHELIX laser's energy is limited to 40 J due to a smaller aperture in the laser beamline. Nevertheless, with a pulse duration of 650 fs (FWHM) and a focal spot size of 3.5 $\mathrm {\mu }$![]() m (FWHM), the laser intensity exceeds $10^{19}\ {\rm W}\ {\rm cm}^{-2}$
m (FWHM), the laser intensity exceeds $10^{19}\ {\rm W}\ {\rm cm}^{-2}$![]() , which is sufficient to accelerate ions to MeV energies. Depending on the desired ion species, different targets are employed. The energy spectrum is exponentially decaying and has a cutoff energy of 28.4 MeV for protons (Busold et al. Reference Busold2013). The accelerated ions exhibit high divergence (up to $30^\circ$
, which is sufficient to accelerate ions to MeV energies. Depending on the desired ion species, different targets are employed. The energy spectrum is exponentially decaying and has a cutoff energy of 28.4 MeV for protons (Busold et al. Reference Busold2013). The accelerated ions exhibit high divergence (up to $30^\circ$![]() half-opening angle) especially for ions with energies well below the cutoff energy ($<$
half-opening angle) especially for ions with energies well below the cutoff energy ($<$![]() 1 MeV u$^{-1}$
1 MeV u$^{-1}$![]() ) which are required for this experiment (Busold Reference Busold2014). To capture and transport the ions, a high-field solenoid positioned on a hexapod within the Z6 target chamber is used. Placing the first solenoid in close proximity to the TNSA target is essential to enhance its capture efficiency. The casing of the solenoid starts 40 mm behind the TNSA target, to allow a motorised stage with a lens and a mirror to be positioned between the TNSA target and the solenoid before each shot, for the adjustment of the PHELIX laser focus. The solenoid's magnetic field strength is adjusted to select and transport the ions of the desired energy with an energy spread of 20 % through the beamline (Busold et al. Reference Busold, Schumacher, Deppert, Brabetz, Kroll, BlaŽević, Bagnoud and Roth2014b). The next component in the beamline is the rf cavity. It is a three-gap spiral resonator that is used for longitudinal manipulation of the ion bunch. Due to the low longitudinal emittance of laser-driven ions, it is possible to reduce their energy spread. For protons with an energy of 8 MeV, it was possible to reduce the energy spread from approximately 20 % after the first solenoid to below 3 % (Busold et al. Reference Busold, Schumacher, Deppert, Brabetz, Kroll, BlaŽević, Bagnoud and Roth2014b, Reference Busold2015) by accelerating the slow ions in the back of the ion bunch and decelerating the fast ions in the front of the ion bunch with the rf cavity. It is also possible to temporally compress the ion bunch to sub-nanosecond bunch durations (Busold et al. Reference Busold2015; Jahn et al. Reference Jahn2019; Metternich et al. Reference Metternich2022) with the same approach by overshooting the energy compression. This results in slower leading ions than trailing ions, which allows the trailing ions to catch up after a certain propagation distance. This methodology will be applied in the stopping power experiment. With this approach, sub-nanosecond ion bunches with an energy spread of 6 % were generated (Metternich et al. Reference Metternich2022). Here the rf cavity will be set up to temporally compress the ions at the middle of the second target chamber called Z4, exactly where the plasma target will be positioned. This is done to reduce the temporal uncertainty of the plasma parameters which rapidly change during the expansion. The efficiency of the rf cavity has a minimum at an energy per mass of 0.5 MeV u$^{-1}$
) which are required for this experiment (Busold Reference Busold2014). To capture and transport the ions, a high-field solenoid positioned on a hexapod within the Z6 target chamber is used. Placing the first solenoid in close proximity to the TNSA target is essential to enhance its capture efficiency. The casing of the solenoid starts 40 mm behind the TNSA target, to allow a motorised stage with a lens and a mirror to be positioned between the TNSA target and the solenoid before each shot, for the adjustment of the PHELIX laser focus. The solenoid's magnetic field strength is adjusted to select and transport the ions of the desired energy with an energy spread of 20 % through the beamline (Busold et al. Reference Busold, Schumacher, Deppert, Brabetz, Kroll, BlaŽević, Bagnoud and Roth2014b). The next component in the beamline is the rf cavity. It is a three-gap spiral resonator that is used for longitudinal manipulation of the ion bunch. Due to the low longitudinal emittance of laser-driven ions, it is possible to reduce their energy spread. For protons with an energy of 8 MeV, it was possible to reduce the energy spread from approximately 20 % after the first solenoid to below 3 % (Busold et al. Reference Busold, Schumacher, Deppert, Brabetz, Kroll, BlaŽević, Bagnoud and Roth2014b, Reference Busold2015) by accelerating the slow ions in the back of the ion bunch and decelerating the fast ions in the front of the ion bunch with the rf cavity. It is also possible to temporally compress the ion bunch to sub-nanosecond bunch durations (Busold et al. Reference Busold2015; Jahn et al. Reference Jahn2019; Metternich et al. Reference Metternich2022) with the same approach by overshooting the energy compression. This results in slower leading ions than trailing ions, which allows the trailing ions to catch up after a certain propagation distance. This methodology will be applied in the stopping power experiment. With this approach, sub-nanosecond ion bunches with an energy spread of 6 % were generated (Metternich et al. Reference Metternich2022). Here the rf cavity will be set up to temporally compress the ions at the middle of the second target chamber called Z4, exactly where the plasma target will be positioned. This is done to reduce the temporal uncertainty of the plasma parameters which rapidly change during the expansion. The efficiency of the rf cavity has a minimum at an energy per mass of 0.5 MeV u$^{-1}$![]() . Therefore, for the stopping power experiment, an energy per mass of 0.6 MeV u$^{-1}$
. Therefore, for the stopping power experiment, an energy per mass of 0.6 MeV u$^{-1}$![]() was targeted. A closer proximity of the rf cavity to the origin of the beam, i.e. the TNSA target, results in the more particles it can temporally compress into the bunch. The minimal distance is limited by the maximum rf cavity voltage and the geometrical constraints at the experimental area Z6 which concludes to a distance of 1225 mm between the TNSA target and the rf cavity. The required cavity voltage for the temporal compression also depends on the distance separating the rf cavity and the plasma target. However, this distance does not have a large effect on the resulting beam parameters. Thus, it is set to 2 m, promoting stable operation of the rf cavity. A second solenoid is used to transversely focus the ion bunch onto the plasma generated in the Z4 target chamber to probe the plasma with as many ions as possible. The optimal placement of the second solenoid depends on the size of the plasma target to be probed by the ion beam. Due to the limited energy of the heating laser (nhelix) and, in turn, the limited focal spot size of 1 mm, the region in which the plasma parameters are spatially homogeneous will only be approximately 0.5 mm in diameter (Cayzac et al. Reference Cayzac2017). Therefore, the second solenoid must focus the ion beam on the plasma to obtain a sufficient quantity of ions to pass through this region. Since the focal spot size increases with the focal length of the solenoid, the distance of the second solenoid to the plasma target should also be kept as short as possible. Unfortunately, the minimum distance achievable is approximately 1 m, as closer proximity would obstruct the path of the heating laser (see figure 3). Before conducting beamtimes with the LIGHT beamline, simulation studies are performed to predict the resulting beam characteristics and requisite beamline settings. The simulation employs numerical solutions of the Lorentz equation to calculate ion trajectories. For comprehensive information on the workings of the LIGHT beamline simulations, refer to Metternich et al. (Reference Metternich2022).
was targeted. A closer proximity of the rf cavity to the origin of the beam, i.e. the TNSA target, results in the more particles it can temporally compress into the bunch. The minimal distance is limited by the maximum rf cavity voltage and the geometrical constraints at the experimental area Z6 which concludes to a distance of 1225 mm between the TNSA target and the rf cavity. The required cavity voltage for the temporal compression also depends on the distance separating the rf cavity and the plasma target. However, this distance does not have a large effect on the resulting beam parameters. Thus, it is set to 2 m, promoting stable operation of the rf cavity. A second solenoid is used to transversely focus the ion bunch onto the plasma generated in the Z4 target chamber to probe the plasma with as many ions as possible. The optimal placement of the second solenoid depends on the size of the plasma target to be probed by the ion beam. Due to the limited energy of the heating laser (nhelix) and, in turn, the limited focal spot size of 1 mm, the region in which the plasma parameters are spatially homogeneous will only be approximately 0.5 mm in diameter (Cayzac et al. Reference Cayzac2017). Therefore, the second solenoid must focus the ion beam on the plasma to obtain a sufficient quantity of ions to pass through this region. Since the focal spot size increases with the focal length of the solenoid, the distance of the second solenoid to the plasma target should also be kept as short as possible. Unfortunately, the minimum distance achievable is approximately 1 m, as closer proximity would obstruct the path of the heating laser (see figure 3). Before conducting beamtimes with the LIGHT beamline, simulation studies are performed to predict the resulting beam characteristics and requisite beamline settings. The simulation employs numerical solutions of the Lorentz equation to calculate ion trajectories. For comprehensive information on the workings of the LIGHT beamline simulations, refer to Metternich et al. (Reference Metternich2022).
To generate the plasma, the nhelix laser is used, as the PHELIX laser is already used to accelerate the ions. For that, the nhelix beam is split into two beams both having an energy of 30 J, a pulse length of 7 ns (FWHM), a wavelength of 527 nm and a focal spot size of 1 mm to achieve plasma parameters similar to those of Cayzac et al. (Reference Cayzac2017). The focus is generated with a random phase plate to achieve an homogeneous spot. The free electron density of the plasma will be measured via interferometry to verify the hydrodynamic simulations of the plasma expansion. These simulations will be used to calculate the stopping power of the ions along the ion path inside the plasma according to the different theoretical models. This is necessary to compare the measurements with the theoretical models. To determine the energy of the ions, a time of flight (ToF) measurement is carried out using an ultrafast diamond membrane detector (Jahn et al. Reference Jahn2018). Due to its radiation hardness and high free charge carrier drift mobility, diamond as the active medium of the detector enables a time resolution of tens of picoseconds.
This experiment represents the first of many stopping power experiments using the infrastructure and platform built at the experimental area Z6 at GSI. The LIGHT beamline can cover a wide parameter space for stopping power experiments by employing various configurations of different targets, plasma parameters and ion beams.
It is planned to conduct this experiment for carbon ions and protons as each have certain advantages over the other. Carbon ions experience approximately 13 times higher energy loss in the plasma as can be seen when inspecting the $y$![]() -axis of the plots in figure 4. Additionally, slow carbon ions are also easier to detect with diamond detectors and scintillators since their energy deposition in the detectors is higher. However, protons have only one charge state which means it is unnecessary to estimate their charge state evolution while travelling through the plasma with theoretical models. For carbon ions, the charge state will change within the plasma and theoretical modelling is required. Consequently, using protons makes modelling the experiment easier. Furthermore, the different theoretical models behave differently for different species (see figure 4) particularly in the stopping maximum. This effect can be better evaluated by using both carbon ions and protons in stopping power experiments.
-axis of the plots in figure 4. Additionally, slow carbon ions are also easier to detect with diamond detectors and scintillators since their energy deposition in the detectors is higher. However, protons have only one charge state which means it is unnecessary to estimate their charge state evolution while travelling through the plasma with theoretical models. For carbon ions, the charge state will change within the plasma and theoretical modelling is required. Consequently, using protons makes modelling the experiment easier. Furthermore, the different theoretical models behave differently for different species (see figure 4) particularly in the stopping maximum. This effect can be better evaluated by using both carbon ions and protons in stopping power experiments.

Figure 4. Different theoretical models for the stopping of (a) carbon ions (C$^{4+}$![]() ) and (b) protons plotted over the ratio of the projectile velocity to the thermal velocity of the free electrons in the plasma. $\text {TM}+\lambda (v)$
) and (b) protons plotted over the ratio of the projectile velocity to the thermal velocity of the free electrons in the plasma. $\text {TM}+\lambda (v)$![]() is the T-Matrix formalism with a velocity dependent screening length (Gericke & Schlanges Reference Gericke and Schlanges2003), LP 3 is the Li–Petrasso model (Zylstra et al. Reference Zylstra2015), Vlasov is the Vlasov model (Peter & Meyer-Ter-Vehn Reference Peter and Meyer-Ter-Vehn1991), RPA is the random phase approximation (Zimmerman Reference Zimmerman1997) and BPS is the Brown Preston Singleton formalism (Brown et al. Reference Brown, Preston and Singleton2005).
is the T-Matrix formalism with a velocity dependent screening length (Gericke & Schlanges Reference Gericke and Schlanges2003), LP 3 is the Li–Petrasso model (Zylstra et al. Reference Zylstra2015), Vlasov is the Vlasov model (Peter & Meyer-Ter-Vehn Reference Peter and Meyer-Ter-Vehn1991), RPA is the random phase approximation (Zimmerman Reference Zimmerman1997) and BPS is the Brown Preston Singleton formalism (Brown et al. Reference Brown, Preston and Singleton2005).
Before conducting such experiments, it is necessary to set up every component and demonstrate its desired functionality. This includes plasma generation with the nhelix laser, which is currently undergoing remodelling to achieve the desired parameters for the experiment. The nhelix laser is scheduled to be completed by December 2023. Additionally, it is important to demonstrate the production of the desired ion beams. To achieve this goal, two preliminary beamtimes were conducted, during which the stopping power in a solid target was measured.
3. Generation of a carbon ion beam
In the following, the results of a preparatory beamtime with carbon ions (C$^{4+}$![]() ) are discussed. As previously mentioned, the goal is to transport carbon ions with an energy of 0.6 MeV u$^{-1}$
) are discussed. As previously mentioned, the goal is to transport carbon ions with an energy of 0.6 MeV u$^{-1}$![]() to compress them temporally to the shortest possible bunch length and to focus the beam transversely in the centre of the Z4 target chamber. The experimental set-up is identical to that of the planned stopping power experiment with diagnostics placed inside the Z4 target chamber instead of the plasma target.
to compress them temporally to the shortest possible bunch length and to focus the beam transversely in the centre of the Z4 target chamber. The experimental set-up is identical to that of the planned stopping power experiment with diagnostics placed inside the Z4 target chamber instead of the plasma target.
To accelerate carbon ions, it is necessary to have a target containing carbon atoms and to get rid of the hydrogen contamination on the surface of the target (Hegelich et al. Reference Hegelich2002). We used a 10 $\mathrm {\mu }$![]() m thick tungsten foil which had a carbon coating on its rear side with a thickness of 0.9 $\mathrm {\mu }$
m thick tungsten foil which had a carbon coating on its rear side with a thickness of 0.9 $\mathrm {\mu }$![]() m. This target was ohmically heated to temperatures above 1000$\,^\circ$
m. This target was ohmically heated to temperatures above 1000$\,^\circ$![]() C, resulting in evaporation of the contaminant layer. A pyrometer was used to measure the temperature of the target to ensure that the heating was sufficient and that the target temperature was reached.
C, resulting in evaporation of the contaminant layer. A pyrometer was used to measure the temperature of the target to ensure that the heating was sufficient and that the target temperature was reached.
To adjust the two solenoids, they were set up to transport protons with an energy of 5.4 MeV, corresponding to the simultaneous transport of C$^{4+}$![]() ions with an energy of 7.2 MeV ( 0.6 MeV u$^{-1}$
ions with an energy of 7.2 MeV ( 0.6 MeV u$^{-1}$![]() ). Using protons to adjust the beamline eliminates the necessity to heat the target for the adjustment process. The radiochromic film (RCF) measurement in figure 5(a) depicts the focal spot of all carbon ions, regardless of their charge state. The achieved focal spot radius, containing 50 % of carbon ions, measured $4.11(2)$
). Using protons to adjust the beamline eliminates the necessity to heat the target for the adjustment process. The radiochromic film (RCF) measurement in figure 5(a) depicts the focal spot of all carbon ions, regardless of their charge state. The achieved focal spot radius, containing 50 % of carbon ions, measured $4.11(2)$![]() mm. This is close to the simulated best possible focal spot radius of 3.9 mm, which is limited by the minimal achievable distance between the second solenoid and the focus position.
mm. This is close to the simulated best possible focal spot radius of 3.9 mm, which is limited by the minimal achievable distance between the second solenoid and the focus position.

Figure 5. Focal spots achieved with the LIGHT beamline of (a) carbon ions (C$^{4+}$![]() ) and (b) protons measured with radiochromic films in the centre of the Z4 target chamber. Depicted in red is the smallest circle that contains 50 % of the deposited energy.
) and (b) protons measured with radiochromic films in the centre of the Z4 target chamber. Depicted in red is the smallest circle that contains 50 % of the deposited energy.
The next step is to temporally compress the bunch with the rf cavity. For that, an ultrafast diamond membrane detector is used to measure the temporal beam profile of the bunch. The detector is placed in the focal spot which is located in the middle of the Z4 target chamber. A scattering foil (2 $\mathrm {\mu }$![]() m Mylar) is placed 300 mm in front of the diamond detector to eliminate the transverse filamentation of the beam which is caused by the imperfections in the magnetic field of the solenoid due to its connection cables (Metternich et al. Reference Metternich2022). The mean scattering angle is 13 mrad for C$^{4+}$
m Mylar) is placed 300 mm in front of the diamond detector to eliminate the transverse filamentation of the beam which is caused by the imperfections in the magnetic field of the solenoid due to its connection cables (Metternich et al. Reference Metternich2022). The mean scattering angle is 13 mrad for C$^{4+}$![]() ions with $E= 7.2$
ions with $E= 7.2$![]() MeV which corresponds to a location deviation of 3.9 mm over the 300 mm distance according to the Stopping and Range of Ions in Matter code (SRIM Ziegler & Biersack Reference Ziegler and Biersack1985). A photodiode next to the diamond detector is used to measure the electromagnetic radiation from the interaction between the PHELIX laser and the TNSA target. The rising edge of the photodiode can be used to determine the start time of the ions. In figure 6, the temporal shape of the bunch with the rf cavity turned off along with the corresponding time of flight signals of the carbon ions in the simulations is shown. The first peak can be assigned to protons, which means the contamination layer was not completely evaporated from the rear side of the target. The next two peaks from left to right correspond to C$^{5+}$
MeV which corresponds to a location deviation of 3.9 mm over the 300 mm distance according to the Stopping and Range of Ions in Matter code (SRIM Ziegler & Biersack Reference Ziegler and Biersack1985). A photodiode next to the diamond detector is used to measure the electromagnetic radiation from the interaction between the PHELIX laser and the TNSA target. The rising edge of the photodiode can be used to determine the start time of the ions. In figure 6, the temporal shape of the bunch with the rf cavity turned off along with the corresponding time of flight signals of the carbon ions in the simulations is shown. The first peak can be assigned to protons, which means the contamination layer was not completely evaporated from the rear side of the target. The next two peaks from left to right correspond to C$^{5+}$![]() and C$^{4+}$
and C$^{4+}$![]() ions. The detector shows no signal where the C$^{3+}$
ions. The detector shows no signal where the C$^{3+}$![]() and the C$^{2+}$
and the C$^{2+}$![]() ions should arrive. Additionally, the peak at 340 ns could be attributed to N$^{4+}$
ions should arrive. Additionally, the peak at 340 ns could be attributed to N$^{4+}$![]() ions with $E=6$
ions with $E=6$![]() MeV (calculated flight time of 358 ns). Nitrogen, oxygen, hydrogen and carbon are part of the contaminant layer. However, it remains unclear why the low energy ions ($\lesssim 0.4\ {\rm MeV}\ {\rm u}^{-1}$
MeV (calculated flight time of 358 ns). Nitrogen, oxygen, hydrogen and carbon are part of the contaminant layer. However, it remains unclear why the low energy ions ($\lesssim 0.4\ {\rm MeV}\ {\rm u}^{-1}$![]() ) are not detected by the diamond detector. According to SRIM, they are not stopped within the 2 $\mathrm {\mu }$
) are not detected by the diamond detector. According to SRIM, they are not stopped within the 2 $\mathrm {\mu }$![]() m thick Mylar foil. Using the Thomson parabola spectra (Ding Reference Ding2018) and the simulations, we determined that the space charge effects for the C$^{3+}$
m thick Mylar foil. Using the Thomson parabola spectra (Ding Reference Ding2018) and the simulations, we determined that the space charge effects for the C$^{3+}$![]() are lower than C$^{4+}$
are lower than C$^{4+}$![]() ions, ruling out those effects as the cause of the missing signal. Therefore, we assume that the diamond detector has difficulty detecting ions with low energies ($\lesssim 0.4\ {\rm MeV}\ {\rm u}^{-1}$
ions, ruling out those effects as the cause of the missing signal. Therefore, we assume that the diamond detector has difficulty detecting ions with low energies ($\lesssim 0.4\ {\rm MeV}\ {\rm u}^{-1}$![]() ). Nonetheless, the data demonstrate the successful transport of C$^{4+}$
). Nonetheless, the data demonstrate the successful transport of C$^{4+}$![]() ions with $E=7.2(2)$
ions with $E=7.2(2)$![]() MeV.
MeV.

Figure 6. Diamond detector signal that corresponds to the time of flight of the ions transported through the LIGHT beamline as well as the time of flight of the transported ions in the simulation. The signals are normalised to the C$^{4+}$![]() peak.
peak.
For the temporal compression of the C$^{4+}$![]() ions, the rf cavity voltage and phase were adjusted incrementally. In figure 7, the shortest diamond detector signal (orange) achieved by this procedure is shown along with the signal of the uncompressed beam (blue) and the temporally compressed beam from the simulation (green). It can be seen that not all transported C$^{4+}$
ions, the rf cavity voltage and phase were adjusted incrementally. In figure 7, the shortest diamond detector signal (orange) achieved by this procedure is shown along with the signal of the uncompressed beam (blue) and the temporally compressed beam from the simulation (green). It can be seen that not all transported C$^{4+}$![]() can be compressed to a single bunch, which is due to the long temporal width of the transported C$^{4+}$
can be compressed to a single bunch, which is due to the long temporal width of the transported C$^{4+}$![]() within the RF cavity. In this case, the temporal width of the transported C$^{4+}$
within the RF cavity. In this case, the temporal width of the transported C$^{4+}$![]() within the rf cavity is even longer than twice the period duration which leads to multiple peaks of the C$^{4+}$
within the rf cavity is even longer than twice the period duration which leads to multiple peaks of the C$^{4+}$![]() at the focal spot in the middle of the Z4 target chamber. The energy transfer from the rf cavity to the ions is velocity dependent due to the three accelerating gaps. This means that other energies are not temporally compressed. For most of the other transported ions, the relative energy transfer is larger, resulting in their temporal compression at a shorter distance. The additional flight distance then leads to a u-shaped temporal profile of the bunch. For the future stopping power experiments, only the temporal compressed carbon ions with an energy of approximately 7.2 MeV are relevant. Since the plasma remains in a relevant state for only 20 ns, it will only affect the desired peak, allowing us to separate the peaks in the measurement. The phase and voltage on each shot are measured to determine the exact cavity settings. In addition, a start detector is used for stopping power experiments to verify the initial energy and ensure accurate measurements. The standard deviation of the measured cavity voltage is 1.23 %, while the measured phase has a standard deviation of $3.1^\circ$
at the focal spot in the middle of the Z4 target chamber. The energy transfer from the rf cavity to the ions is velocity dependent due to the three accelerating gaps. This means that other energies are not temporally compressed. For most of the other transported ions, the relative energy transfer is larger, resulting in their temporal compression at a shorter distance. The additional flight distance then leads to a u-shaped temporal profile of the bunch. For the future stopping power experiments, only the temporal compressed carbon ions with an energy of approximately 7.2 MeV are relevant. Since the plasma remains in a relevant state for only 20 ns, it will only affect the desired peak, allowing us to separate the peaks in the measurement. The phase and voltage on each shot are measured to determine the exact cavity settings. In addition, a start detector is used for stopping power experiments to verify the initial energy and ensure accurate measurements. The standard deviation of the measured cavity voltage is 1.23 %, while the measured phase has a standard deviation of $3.1^\circ$![]() , equivalent to a 0.08 ns delay. The deviation in voltage affects only the bunch length, whereas the deviation in phase affects both the bunch length and the temporally compressed energy. We simulated a translated standard deviation of 642 eV u$^{-1}$
, equivalent to a 0.08 ns delay. The deviation in voltage affects only the bunch length, whereas the deviation in phase affects both the bunch length and the temporally compressed energy. We simulated a translated standard deviation of 642 eV u$^{-1}$![]() in energy and 100 ps in pulse length.
in energy and 100 ps in pulse length.

Figure 7. Measured and simulated time of flight of the temporally compressed C$^{4+}$![]() ions along with the measured time of flight of the uncompressed C$^{4+}$
ions along with the measured time of flight of the uncompressed C$^{4+}$![]() ions.
ions.
The flight times and temporal distributions of the various carbon ion bunches exhibit only minor variations. The shortest bunch duration is $\tau = 1.23(4)$![]() ns (FWHM), which is four times larger than predicted by simulations (see table 1). A range of potential causes, including the scattering foil in ToF measurements, space charge effects, the TNSA-generated ion beam's non-negligible initial emittance and the radial dependency of the electric field within the rf cavity gaps, were thoroughly examined. However, these factors do not appear to explain the observed phenomenon. Saturation effects in the diamond detector could be a plausible cause. This hypothesis requires confirmation through further testing of the diamond detector with lower fluxes and other diagnostics during future beamtimes.
ns (FWHM), which is four times larger than predicted by simulations (see table 1). A range of potential causes, including the scattering foil in ToF measurements, space charge effects, the TNSA-generated ion beam's non-negligible initial emittance and the radial dependency of the electric field within the rf cavity gaps, were thoroughly examined. However, these factors do not appear to explain the observed phenomenon. Saturation effects in the diamond detector could be a plausible cause. This hypothesis requires confirmation through further testing of the diamond detector with lower fluxes and other diagnostics during future beamtimes.
Table 1. Comparison between simulated and measured parameters of the temporally compressed carbon bunch.

To estimate the number of transported carbon ions, an HD-V2 RCF by Ashland positioned at the location of the diamond detector (see figure 5a) measures the deposited energy of the temporally compressed ion beam. The active layer of this RCF has a thickness of 10 $\mathrm {\mu }$![]() m. During the experiment, the active layer was exposed to the incident beam without any passive layer in front of it. It is assumed that the total energy deposited in the active layer corresponds to the energy of all transported carbon and nitrogen ions. The deposited energy of protons in this layer can be neglected, as those with an energy of 5.25 MeV are not stopped in this layer and lose minimal energy ($\approx 8$
m. During the experiment, the active layer was exposed to the incident beam without any passive layer in front of it. It is assumed that the total energy deposited in the active layer corresponds to the energy of all transported carbon and nitrogen ions. The deposited energy of protons in this layer can be neglected, as those with an energy of 5.25 MeV are not stopped in this layer and lose minimal energy ($\approx 8$![]() keV per proton). For the estimation, the energy spectrum of the carbon ions from the simulation was used as the diamond detector faced difficulties in detecting lower energies, rendering it incapable of measuring the spectrum. The transported beam in the simulation, which uses the Thomson parabola spectra measured by Ding (Reference Ding2018) for the TNSA source, comprises 21 % C$^{2+}$
keV per proton). For the estimation, the energy spectrum of the carbon ions from the simulation was used as the diamond detector faced difficulties in detecting lower energies, rendering it incapable of measuring the spectrum. The transported beam in the simulation, which uses the Thomson parabola spectra measured by Ding (Reference Ding2018) for the TNSA source, comprises 21 % C$^{2+}$![]() , 26 % C$^{3+}$
, 26 % C$^{3+}$![]() , 40 % C$^{4+}$
, 40 % C$^{4+}$![]() and 13 % C$^{5+}$
and 13 % C$^{5+}$![]() ions. The total energy deposited in the active layer amounts to $E_\text {dep}=2.0(6)\times 10^{10}$
ions. The total energy deposited in the active layer amounts to $E_\text {dep}=2.0(6)\times 10^{10}$![]() MeV, with the significant uncertainty stemming from a lack of calibration in the used RCF lot, which required us to use a calibration from an older lot. Under the assumption that the spectrum of the measured beam corresponds to the spectrum obtained from simulations, the transported ion beam comprises $3.6(1.1)\times 10^{9}$
MeV, with the significant uncertainty stemming from a lack of calibration in the used RCF lot, which required us to use a calibration from an older lot. Under the assumption that the spectrum of the measured beam corresponds to the spectrum obtained from simulations, the transported ion beam comprises $3.6(1.1)\times 10^{9}$![]() carbon ions, of which $1.4(4)\times 10^{9}$
carbon ions, of which $1.4(4)\times 10^{9}$![]() are C$^{4+}$
are C$^{4+}$![]() ions. Furthermore, simulations indicate that 14 % of the transported C$^{4+}$
ions. Furthermore, simulations indicate that 14 % of the transported C$^{4+}$![]() ions can be temporally compressed, equating to $2.0(6)\times 10^{8}$
ions can be temporally compressed, equating to $2.0(6)\times 10^{8}$![]() temporally compressed C$^{4+}$
temporally compressed C$^{4+}$![]() ions in the experiment.
ions in the experiment.
In table 1, the most important parameters of the final carbon bunch are summarised and compared with the simulation.
4. Generation of a proton beam
In this section, the results of the preparatory beamtime for protons are discussed. The goal of this second preparatory beamtime was to transport protons with an energy of 0.6 MeV and to compress them temporally to the shortest possible bunch length. The experimental set-up is identical to the carbon ion beamtime. In addition, simulations were conducted prior to this beamtime.
Heating the target is not required for proton acceleration. A range of TNSA targets was used to determine the most suitable target for the stopping power experiment. Both 10 $\mathrm {\mu }$![]() m gold and 10 $\mathrm {\mu }$
m gold and 10 $\mathrm {\mu }$![]() m tungsten targets were tested, with no observable differences in behaviour. Additionally, we tested 500 nm polystyrene targets, which demonstrated a notable decrease in the electromagnetic pulse (EMP) detected by our time of flight diagnostics. Typically, the targets are mounted on an aluminium holder; we replaced it with a 3-D printed PETG (polyethylene terephthalate glycol-modified) holder. This also significantly reduced the noise caused by the EMP, particularly for the time of flight signal measured with a scintillator (BC-422Q by Saint-Gobain Crystals) and a photodiode (AXUV20HS1 by Optodiode), as demonstrated in figure 8.
m tungsten targets were tested, with no observable differences in behaviour. Additionally, we tested 500 nm polystyrene targets, which demonstrated a notable decrease in the electromagnetic pulse (EMP) detected by our time of flight diagnostics. Typically, the targets are mounted on an aluminium holder; we replaced it with a 3-D printed PETG (polyethylene terephthalate glycol-modified) holder. This also significantly reduced the noise caused by the EMP, particularly for the time of flight signal measured with a scintillator (BC-422Q by Saint-Gobain Crystals) and a photodiode (AXUV20HS1 by Optodiode), as demonstrated in figure 8.

Figure 8. Comparison of the signals of a diamond detector used as the stop detector and a scintillator with a photodiode used as the start detector in ToF measurements affected by EMP when using (a) a metal target on a metal holder versus (b) a plastic target on a plastic holder. The multipeak structure is due to the bunching of the rf cavity.
After adjusting the two solenoids, the achieved focal spot was measured with an RCF and can be seen in figure 5(b). A focal spot radius of $2.82(3)$![]() mm which contained 50 % of the protons was achieved.
mm which contained 50 % of the protons was achieved.
The temporal beam profile of the proton bunch is measured with the ultrafast diamond membrane detector and again a scattering foil was used to disrupt the transverse filamentation of the beam. The signal of the diamond detector is depicted in figure 9(a) in conjunction with the simulated proton bunch. The protons with an energy of 0.6 MeV are anticipated to arrive at approximately $t= 295$![]() ns. It can be seen that the diamond detector had problems detecting the slow protons, thus strengthening the assumption that its efficiency in detecting low-energy particles is questionable. To ensure that the magnets were transporting protons at the correct energy of 0.6 MeV, an RCF measurement was carried out. In front of the active layer of the RCF, Mylar foils of different thicknesses were placed to stop all protons up to a certain energy. Figure 9(b) shows the RCF with three segments. The 12 $\mathrm {\mu }$
ns. It can be seen that the diamond detector had problems detecting the slow protons, thus strengthening the assumption that its efficiency in detecting low-energy particles is questionable. To ensure that the magnets were transporting protons at the correct energy of 0.6 MeV, an RCF measurement was carried out. In front of the active layer of the RCF, Mylar foils of different thicknesses were placed to stop all protons up to a certain energy. Figure 9(b) shows the RCF with three segments. The 12 $\mathrm {\mu }$![]() m Mylar foil stops all protons with an energy lower than 0.7 MeV ($t> 281$
m Mylar foil stops all protons with an energy lower than 0.7 MeV ($t> 281$![]() ns), which is a substantial amount, as can be seen. The 6 $\mathrm {\mu }$
ns), which is a substantial amount, as can be seen. The 6 $\mathrm {\mu }$![]() m Mylar foil stops all protons with an energy lower than 0.45 MeV ($t> 351$
m Mylar foil stops all protons with an energy lower than 0.45 MeV ($t> 351$![]() ns) and in the third segment, all protons lose energy. Since the segment with the 6 $\mathrm {\mu }$
ns) and in the third segment, all protons lose energy. Since the segment with the 6 $\mathrm {\mu }$![]() m Mylar foil shows a significant number of protons, we can be sure that protons with an energy between 0.45 MeV and 0.7 MeV ($281\ {\rm ns}< t< 351$
m Mylar foil shows a significant number of protons, we can be sure that protons with an energy between 0.45 MeV and 0.7 MeV ($281\ {\rm ns}< t< 351$![]() ns) were transported. In the segment without Mylar, all protons deposit their energy in the active layer. This indicates that, in addition to the targeted proton energies, slower protons are also reaching the end of the beamline. It is evident that these slower protons are not being perfectly transported by solenoids. However, since there are more slower protons in the TNSA spectrum, they exhibit a strong dose on the RCF. Upon turning the rf cavity on, the intensity of the proton bunch with an energy of $0.63(1)$
ns) were transported. In the segment without Mylar, all protons deposit their energy in the active layer. This indicates that, in addition to the targeted proton energies, slower protons are also reaching the end of the beamline. It is evident that these slower protons are not being perfectly transported by solenoids. However, since there are more slower protons in the TNSA spectrum, they exhibit a strong dose on the RCF. Upon turning the rf cavity on, the intensity of the proton bunch with an energy of $0.63(1)$![]() MeV increased due to the temporal compression. This consequently enabled detection by the diamond detector. So it was possible to adjust the rf cavity's voltage and phase to reach optimal temporal compression. We achieved the shortest bunch duration of 0.76(4) ns as shown in figure 10 along with the simulated shortest bunch. While the flight times and temporal distributions exhibit minimal deviations, the experimental bunch duration again exceeds the simulated bunch duration (see table 2) which is likely caused by saturation effects of the diamond detector.
MeV increased due to the temporal compression. This consequently enabled detection by the diamond detector. So it was possible to adjust the rf cavity's voltage and phase to reach optimal temporal compression. We achieved the shortest bunch duration of 0.76(4) ns as shown in figure 10 along with the simulated shortest bunch. While the flight times and temporal distributions exhibit minimal deviations, the experimental bunch duration again exceeds the simulated bunch duration (see table 2) which is likely caused by saturation effects of the diamond detector.

Figure 9. (a) Diamond detector signal that corresponds to the time of flight of the protons that are transported through the LIGHT beamline as well as the time of flight of the transported protons in the simulation. (b) RCF measurement of proton beam with three segments: one with no Mylar foil, one with 6 $\mathrm {\mu }$![]() m (${>}0.45$
m (${>}0.45$![]() MeV) and one with 12 $\mathrm {\mu }$
MeV) and one with 12 $\mathrm {\mu }$![]() m Mylar (${>}0.7$
m Mylar (${>}0.7$![]() MeV) in front of it. In the middle of the RCF, there is a hole and a piece of tape.
MeV) in front of it. In the middle of the RCF, there is a hole and a piece of tape.

Figure 10. Measured and simulated time of flight of the temporally compressed protons.
Table 2. Comparison between simulated and measured parameters of the temporally compressed proton bunch.

Due to our incomplete understanding of the response of the diamond detector at low energies, we cannot assume that the energy deposited on the RCF is dominated by the protons with an energy of 0.63(1) MeV. Instead, we approximated the number of transported protons by modelling their propagation through the beamline using the proton distribution at the TNSA source, which we measured using radiochromic imaging spectroscopy (RIS) (Schmitz, Metternich & Boine-Frankenheim Reference Schmitz, Metternich and Boine-Frankenheim2022). This estimation results in $5.8(4) \times 10^{8}$![]() temporally compressed protons.
temporally compressed protons.
In table 2, the most important parameters of the final proton bunch are summarised and compared with the simulation.
5. Stopping power in cold foil
During the proton beamtime, we conducted an experiment on stopping power using a cold carbon foil which will be reported in this section. For the stopping power experiment, the transported protons passed through a scintillator with a hole in it (see figure 11). This ensured that the protons located on the periphery of the beam were stopped in the scintillator and detected with a photodiode that provided the start signal for the ToF measurement. The scintillator used was a BC-422Q by Saint-Gobain Crystals, and the signal was detected with an AXUV20HS1 photodiode by Optodiode. The protons that passed through the aperture lost energy within the carbon foil located in the focal spot of the proton beam. Following a time of flight distance of $d_\text {ToF}=0.818(2)$![]() m, a diamond detector with an area of $10 \times 10\ {\rm mm}^{2}$
m, a diamond detector with an area of $10 \times 10\ {\rm mm}^{2}$![]() and with a thickness of 19 $\mathrm {\mu }$
and with a thickness of 19 $\mathrm {\mu }$![]() m was employed to measure the stop signal. A scattering foil (1 $\mathrm {\mu }$
m was employed to measure the stop signal. A scattering foil (1 $\mathrm {\mu }$![]() m thick Mylar) in front of the scintillator was used to disrupt the filamentation of the beam. The stopping target was a carbon foil with an areal density of $105\ \mathrm {\mu }{\rm g}\ {\rm cm}^{-2}$
m thick Mylar) in front of the scintillator was used to disrupt the filamentation of the beam. The stopping target was a carbon foil with an areal density of $105\ \mathrm {\mu }{\rm g}\ {\rm cm}^{-2}$![]() . Two shots without and two shots with the stopping target were conducted to measure the energy loss of the protons in the carbon foil. Figure 12 illustrates the time signals of the start and stop detectors for a shot without and with the carbon foil.
. Two shots without and two shots with the stopping target were conducted to measure the energy loss of the protons in the carbon foil. Figure 12 illustrates the time signals of the start and stop detectors for a shot without and with the carbon foil.

Figure 11. Schematic illustration of the stopping power experiment with the LIGHT beamline in a cold carbon foil.

Figure 12. Time of flight measurements of the proton energy with a scintillator (start) and a diamond detector (stop). (a) Time of flight measurement of initial proton energy without carbon foil. (b) Time of flight measurement of final proton energy with carbon foil. The dashed lines show the centre of weight of the protons used for the stopping power measurement.
The signal of the scintillator was deconvolved with the response function of the AXUV photodiode which was measured with a short pulse laser. The response of the scintillator and the diamond detector were not considered since both of them have fast rise and fall times (${\approx }10^{-9}$![]() s). The shots without the carbon foil are used to measure the initial energy of the proton bunch. The central energy was obtained by using the peaks’ centre of weights. An initial energy of $E_{i}=595(5)$
s). The shots without the carbon foil are used to measure the initial energy of the proton bunch. The central energy was obtained by using the peaks’ centre of weights. An initial energy of $E_{i}=595(5)$![]() keV was determined. The final energy was determined with the two shots in which the protons passed through the carbon foil. The signal was observed to shift towards later times, indicating a reduction in the energy of the protons. An energy of $E_{f}=566(4)$
keV was determined. The final energy was determined with the two shots in which the protons passed through the carbon foil. The signal was observed to shift towards later times, indicating a reduction in the energy of the protons. An energy of $E_{f}=566(4)$![]() keV was determined. Using the measured initial energy of the protons, it is possible to calculate their energy after passing through the stopping foil with SRIM, which concludes to $E_{f,\text {SRIM}}=563(12)$
keV was determined. Using the measured initial energy of the protons, it is possible to calculate their energy after passing through the stopping foil with SRIM, which concludes to $E_{f,\text {SRIM}}=563(12)$![]() keV. Since the calculated energy and the measured energy of the protons after passing through the carbon foil are within each other's error bars, we can claim a successful stopping power experiment in a cold foil. We recorded an energy loss of $dE= 29(6)$
keV. Since the calculated energy and the measured energy of the protons after passing through the carbon foil are within each other's error bars, we can claim a successful stopping power experiment in a cold foil. We recorded an energy loss of $dE= 29(6)$![]() keV with an uncertainty of 20 %. According to theoretical models, we anticipate that the protons will lose approximately 70–100 keV in the plasma aimed for in the planned experiment ($E =2\times 30$
keV with an uncertainty of 20 %. According to theoretical models, we anticipate that the protons will lose approximately 70–100 keV in the plasma aimed for in the planned experiment ($E =2\times 30$![]() J, $\lambda = 527$
J, $\lambda = 527$![]() nm, $\tau = 7$
nm, $\tau = 7$![]() ns (FWHM), $d= 1$
ns (FWHM), $d= 1$![]() mm). We expect a reduced uncertainty of approximately 5 keV because the flight time will be longer. For 70 keV, the resulting uncertainty is 7 %. The calculation of stopping power along the ion path, according to theoretical models, will have an uncertainty due to the uncertainty of plasma parameters. The plasma parameters along the ion path are simulated using a hydrodynamic code and verified with interferometric measurements of the free electron density. Based on previous experiments, this uncertainty in calculated energy loss is approximately 10 % (Cayzac et al. Reference Cayzac2017). This is sufficient to benchmark theoretical models, which show discrepancies of up to 26 % (see figure 4).
mm). We expect a reduced uncertainty of approximately 5 keV because the flight time will be longer. For 70 keV, the resulting uncertainty is 7 %. The calculation of stopping power along the ion path, according to theoretical models, will have an uncertainty due to the uncertainty of plasma parameters. The plasma parameters along the ion path are simulated using a hydrodynamic code and verified with interferometric measurements of the free electron density. Based on previous experiments, this uncertainty in calculated energy loss is approximately 10 % (Cayzac et al. Reference Cayzac2017). This is sufficient to benchmark theoretical models, which show discrepancies of up to 26 % (see figure 4).
6. Conclusion and outlook
In this article, the results of two beamtimes performed as preparation for the planned stopping power experiments in plasma with the LIGHT beamline were presented. They showed the capability of the beamline to generate the required ion beams. Carbon ions (C$^{4+}$![]() ) with an energy of 7.2(2) MeV were successfully transported and temporally compressed to a bunch duration of 1.23(4) ns (FWHM). Also, protons with an energy of 0.63(1) MeV were transported and temporally compressed to a bunch duration of 0.76(4) ns. All the bunch characteristics are summarised in tables 1 and 2. The transported protons were used to perform a stopping power experiment in a solid carbon foil. We measured an energy loss of $dE= 29(6)$
) with an energy of 7.2(2) MeV were successfully transported and temporally compressed to a bunch duration of 1.23(4) ns (FWHM). Also, protons with an energy of 0.63(1) MeV were transported and temporally compressed to a bunch duration of 0.76(4) ns. All the bunch characteristics are summarised in tables 1 and 2. The transported protons were used to perform a stopping power experiment in a solid carbon foil. We measured an energy loss of $dE= 29(6)$![]() keV, which agrees with the energy loss predicted by SRIM.
keV, which agrees with the energy loss predicted by SRIM.
The next step is to conduct the planned stopping power experiment with a plasma target. This will allow for theory benchmarking in the regime of the stopping maximum.
Acknowledgements
The authors would like to express their gratitude to the PHELIX laser team for their support, as well as to the HF group of GSI for their assistance. Additionally, the target laboratory at Technische Universität Darmstadt (T. Abel and G. Schaumann) and the target laboratory at GSI are acknowledged for their contributions to target fabrication. The detector laboratory of GSI (M. Träger and M. Kis) is also appreciated for their work on detector development. Finally, the work of the high-field laboratory (HLD) at HZDR for the solenoid construction is also acknowledged. The referees are acknowledged for their valuable comments that have significantly improved the quality of this article.
Editor Per Helander thanks the referees for their advice in evaluating this article.
Declaration of interest
The authors report no conflict of interest.
Data availability
The authors confirm that all of the data and codes used in this study are available from the corresponding author upon reasonable request.