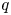1 Introduction
In recent years, the interaction between a dusty plasma and the wall has been the focus of a great deal of scientific research in basic plasma physics, because of its importance in various fields, as plasma processing technologies like plasma source ion implantation (Conrad et al. Reference Conrad, Radtke, Dodd, Worzala and Tran1987), plasma etching of semiconductor devices (Abe, Yoneda & Fujiwara Reference Abe, Yoneda and Fujiwara2008) and plasma medicine (Weltmann & Woedtke Reference Weltmann and Woedtke2017), as well as controlled fusion devices (Krasheninnikov et al. Reference Krasheninnikov, Smirnov and Rudakov2011). In fact, understanding the structure of the region between the dusty plasma and the wall and the dynamics that govern it has become a challenge for scientific researchers. The description of plasma sheaths that join plasmas to their boundaries is a most interesting subject in the field of plasma research. Thus, the extensive distribution function has been employed to investigate the different aspects of plasma physics including a dusty plasma sheath. In this context, the distribution functions of electrons is assumed to be of Maxwellian type (Yu, Saleem & Luo Reference Yu, Saleem and Luo1992; Ma & Yu Reference Ma and Yu1995; Arnas et al. Reference Arnas, Mikikian, Bachet and Doveil2000; Liu, Wang & Ma Reference Liu, Wang and Ma2000; Mahanta & Goswami Reference Mahanta and Goswami2001; Kalita & Das Reference Kalita and Das2003; Liu et al. Reference Liu, Zhang, Zou, Wang, Liu, Wang and Gong2004; Wang et al. Reference Wang, Liu, Ren, Liu and Wang2006; Xiu Reference Xiu2006; Foroutan, Mehdipour & Zahed Reference Foroutan, Mehdipour and Zahed2009; Masoudi, Jafari & Shorakaee Reference Masoudi, Jafari and Shorakaee2009; Foroutan Reference Foroutan2010; Mehdipour, Denysenko & Ostrikov Reference Mehdipour, Denysenko and Ostrikov2010; Benlemdjaldi et al. Reference Benlemdjaldi, Tahraoui, Hugon and Bougdira2013; Driouch & Chatei Reference Driouch and Chatei2013; Driouch, Chatei & Bojaddaini Reference Driouch, Chatei and Bojaddaini2015; Nafari, Ghoranneviss & Yasserian Reference Nafari, Ghoranneviss and Yasserian2015; Ou, Zhao & Lin Reference Ou, Zhao and Lin2018), where long-range interactions are considered negligible in such systems. However, it has been reported recently that the plasma system far away from equilibrium and the electron energy distribution departs significantly from the Maxwellian distribution. In this case, the above Boltzmann–Gibbs theory is inapplicable because of the contribution of long-range interactions that should not be overlooked. To resolve such problems, Tsallis (Reference Tsallis1988) proposed the non-extensive statistic as a generalisation of the Boltzmann–Gibbs one.
This new statistic is based on a parameter $q$![]() quantifying the degree of a non-extensivity of the system. We note that if $q\neq 1$
quantifying the degree of a non-extensivity of the system. We note that if $q\neq 1$![]() , it gives the power-law distribution function, where there are two cases $q<1$
, it gives the power-law distribution function, where there are two cases $q<1$![]() (superextensivity) and $q>1$
(superextensivity) and $q>1$![]() (subextensivity), whereas if $q=1$
(subextensivity), whereas if $q=1$![]() , the distribution function reduces to that of the celebrated $BG$
, the distribution function reduces to that of the celebrated $BG$![]() extensive.
extensive.
In the context of non-extensive electrons, a great deal of work has been done (Liu, Liu & Zou Reference Liu, Liu and Zou2013; Safa, Ghomi & Niknam Reference Safa, Ghomi and Niknam2014; Sharifian et al. Reference Sharifian, Sharifinejad, BorhaniZarandi and Niknam2014; Hatami Reference Hatami2015; Driouch & Chatei Reference Driouch and Chatei2017; Hesar, Kalejahi & Moghanjoughi Reference Hesar, Kalejahi and Moghanjoughi2017; Borgohain & Saharia Reference Borgohain and Saharia2018; El Ghani, Driouch & Chatei Reference El Ghani, Driouch and Chatei2019; Khalilpour & Foroutan Reference Khalilpour and Foroutan2019). Driouch & Chatei (Reference Driouch and Chatei2017) investigated the effect of the non-extensivity $q$![]() -parameter on the plasma sheath parameters, which showed that there is a significant change in the quantities characterising the sheath when the electrons evolve far away from their thermodynamic equilibrium. Taking into account the ion–neutral collisions, Hatami (Reference Hatami2015) studied the velocity of positive ions at the sheath edge, and found that the degree of non-extensivity of electrons ($q$
-parameter on the plasma sheath parameters, which showed that there is a significant change in the quantities characterising the sheath when the electrons evolve far away from their thermodynamic equilibrium. Taking into account the ion–neutral collisions, Hatami (Reference Hatami2015) studied the velocity of positive ions at the sheath edge, and found that the degree of non-extensivity of electrons ($q$![]() ) affects the lower limit of the entrance velocity of ions into the sheath and its values can be greater or smaller than its Maxwellian counterpart. Recently, Zou et al. (Reference Zou, Liu, Zhu, Zhang and Qiu2020) emphasised the effect of non-extensive electron distribution on the electronegative plasma sheath structure, where it is revealed that the non-extensive parameter $q$
) affects the lower limit of the entrance velocity of ions into the sheath and its values can be greater or smaller than its Maxwellian counterpart. Recently, Zou et al. (Reference Zou, Liu, Zhu, Zhang and Qiu2020) emphasised the effect of non-extensive electron distribution on the electronegative plasma sheath structure, where it is revealed that the non-extensive parameter $q$![]() has a significant influence on the structure of the electronegative magnetised plasma sheath. Moreover, the experiments suggest that the electrons should be considered superextensive ($q<1$
has a significant influence on the structure of the electronegative magnetised plasma sheath. Moreover, the experiments suggest that the electrons should be considered superextensive ($q<1$![]() ), which means that they are more energetic than Boltzmann electrons. Due to the presence of these highly energetic electrons, it is important to recognise their significantly increased energy levels. This elevated energy can reach the necessary threshold of 50 eV for inducing a powerful emission of secondary electrons from dust particles (Meyer-Vernet Reference Meyer-Vernet1982; Tolias et al. Reference Tolias, Komm, Ratynskaia and Podolnik2020; Long & Ou Reference Long and Ou2022). Some of the primary electrons are reflected elastically ($\textit {backscattered electrons}$
), which means that they are more energetic than Boltzmann electrons. Due to the presence of these highly energetic electrons, it is important to recognise their significantly increased energy levels. This elevated energy can reach the necessary threshold of 50 eV for inducing a powerful emission of secondary electrons from dust particles (Meyer-Vernet Reference Meyer-Vernet1982; Tolias et al. Reference Tolias, Komm, Ratynskaia and Podolnik2020; Long & Ou Reference Long and Ou2022). Some of the primary electrons are reflected elastically ($\textit {backscattered electrons}$![]() ), while the rest penetrate the material. Some of last electrons are scattered and reflected by one or more atoms in the material, and these are the so-called ‘$\textit {inelastic reflection}$
), while the rest penetrate the material. Some of last electrons are scattered and reflected by one or more atoms in the material, and these are the so-called ‘$\textit {inelastic reflection}$![]() ’ electrons. The remaining electrons interact with the material in a more complex manner, generating the so-called ‘$\textit {true secondary}$
’ electrons. The remaining electrons interact with the material in a more complex manner, generating the so-called ‘$\textit {true secondary}$![]() ’ electrons.
’ electrons.
Consequently, disregarding the influence exerted by the current of secondary emission on the sheath configuration would be a serious oversight, leading to erroneous conclusions and compromising the overall accuracy of the analysis.
In the framework of superextensive electrons, there are numerous theoretical studies aimed at examining the sheath structure (Basnet, Ram Pokhrel & Khanal Reference Basnet, Ram Pokhrel and Khanal2021; Paul et al. Reference Paul, Deka, Sharma, Moulick, Adhikari, Kausik and Saikia2023), and further work taking into account secondary electron emission and its effect on different aspects of dusty plasma sheath. These studies have been carried out taking into account only true-secondary electron emission (El Ghani, Driouch & Chatei Reference El Ghani, Driouch and Chatei2020) by calculating the SEE rate from the dust particle. However, at low energies of incident electrons ($E<50$![]() eV), the secondary emission from dust grains (such as tungsten particles) may be generated by the various ways of contributions coming from backscattered electron emission (BEE), inelastic reflection emission (IRE) as well as true-secondary electron emission (TEE). In this context, Ou & Long (Reference Ou and Long2023) investigate the evolution of the dust surface potential of a tungsten particle in bulk plasma using the model developed by Furman and Pivi (F-P model), which involves all the types of secondary electron emissions mentioned above, it is clearly shown that the contribution of BEE and IRE in secondary electron emission from dust particles cannot be underestimated (Tolias Reference Tolias2016). For this reason, some extension of secondary emission should be needed to investigate its impact in the sheath of dusty plasma. In fact, the present work is aimed at studying the effect of SEE, including these three modes of electron emissions, on the structure of a tungsten dusty plasma sheath containing superextensive electrons.
eV), the secondary emission from dust grains (such as tungsten particles) may be generated by the various ways of contributions coming from backscattered electron emission (BEE), inelastic reflection emission (IRE) as well as true-secondary electron emission (TEE). In this context, Ou & Long (Reference Ou and Long2023) investigate the evolution of the dust surface potential of a tungsten particle in bulk plasma using the model developed by Furman and Pivi (F-P model), which involves all the types of secondary electron emissions mentioned above, it is clearly shown that the contribution of BEE and IRE in secondary electron emission from dust particles cannot be underestimated (Tolias Reference Tolias2016). For this reason, some extension of secondary emission should be needed to investigate its impact in the sheath of dusty plasma. In fact, the present work is aimed at studying the effect of SEE, including these three modes of electron emissions, on the structure of a tungsten dusty plasma sheath containing superextensive electrons.
The paper is organised as follows. In § 2, the basic equations and assumptions of the multifluid sheath model are introduced, and the numerical method is noted. In § 3, we present the results of numerical simulations of the model equations, and brief analyses are made. The paper is finished in § 4 with a conclusion and brief discussion of the main findings.
2 Model and basic equations
In this section, we indicate the model and the basic equations that describe the structure of the magnetised dusty plasma sheath in the presence of superextensive primary electrons, cold ions and dust of variable charge.
The evolution of the physical parameters is assumed to be changed in one direction ($x$![]() -axis), while the other two directions $(y,z)$
-axis), while the other two directions $(y,z)$![]() are considered infinite (see figure 1). However, the movement of ions and dust is three-dimensional, i.e. $\boldsymbol{\mathsf{v}_j}={\mathsf {v}_{xj}} {\mathsf{x}} +{\mathsf{v}_{yj}} {\mathsf{y}}+{\mathsf{v}_{zj}} {\mathsf{z}}$
are considered infinite (see figure 1). However, the movement of ions and dust is three-dimensional, i.e. $\boldsymbol{\mathsf{v}_j}={\mathsf {v}_{xj}} {\mathsf{x}} +{\mathsf{v}_{yj}} {\mathsf{y}}+{\mathsf{v}_{zj}} {\mathsf{z}}$![]() , where $(j=i)$
, where $(j=i)$![]() for ions and $(j=d)$
for ions and $(j=d)$![]() for dust.
for dust.

Figure 1. The geometry of the considered sheath model.
As shown in figure 1, the magnetic field, which is spatially uniform and constant in time, is made at the $(x,y)$![]() plane and its vector is defined by the following expression: $\boldsymbol {B}=B[\cos (\theta )\boldsymbol {x}+\sin (\theta )\boldsymbol {y}]$
plane and its vector is defined by the following expression: $\boldsymbol {B}=B[\cos (\theta )\boldsymbol {x}+\sin (\theta )\boldsymbol {y}]$![]() .
.
The dusty plasma is considered to be quasineutral at the sheath edge $(x=0)$![]() :
:
where $e$![]() is the electron charge and $q_{d0}$
is the electron charge and $q_{d0}$![]() is the dust charge at the sheath edge. Here, $n_{i0}$
is the dust charge at the sheath edge. Here, $n_{i0}$![]() , $n_{e0}$
, $n_{e0}$![]() and $n_{d0}$
and $n_{d0}$![]() are the ion, electron and dust densities, respectively, at the sheath edge.
are the ion, electron and dust densities, respectively, at the sheath edge.
We assume that the primary electrons are superextensive and obey the $q$![]() -non-extensive distribution function (Lima, Bezerra & Silva Reference Lima, Bezerra and Silva2002a; Lima, Silva & Santos Reference Lima, Silva and Santos2002b).
-non-extensive distribution function (Lima, Bezerra & Silva Reference Lima, Bezerra and Silva2002a; Lima, Silva & Santos Reference Lima, Silva and Santos2002b).

where $C_q$![]() is a normalisation constant. Its expression depends on parameter $q$
is a normalisation constant. Its expression depends on parameter $q$![]() and standard gamma function $\varGamma$
and standard gamma function $\varGamma$![]() , given by
, given by

where $v_e$![]() , $m_e$
, $m_e$![]() , $T_e$
, $T_e$![]() and $n_{e_0}$
and $n_{e_0}$![]() are velocity, mass, temperature (in $eV$
are velocity, mass, temperature (in $eV$![]() ) and non-perturbed density of the electrons, respectively, and $\phi (x)$
) and non-perturbed density of the electrons, respectively, and $\phi (x)$![]() is the electrostatic potential.
is the electrostatic potential.
Here, the electron density take the form (Safa et al. Reference Safa, Ghomi and Niknam2014):

The cold positive ions satisfy the continuity equation:
and that of the momentum conservation:
where $\boldsymbol {v_i}$![]() , $n_i$
, $n_i$![]() and $m_i$
and $m_i$![]() are the velocity, density and mass of the positive ion species in the sheath, respectively.
are the velocity, density and mass of the positive ion species in the sheath, respectively.
The dust grains are treated as cold fluid under the effect of the electric, magnetic and gravitational forces, as well as the ion and neutral drag forces. Their fluid equations are written as follows:
where $q_d$![]() is the variable charge of the dust grain, and $m_d$
is the variable charge of the dust grain, and $m_d$![]() , $n_d$
, $n_d$![]() and $\boldsymbol {v_d}$
and $\boldsymbol {v_d}$![]() are the mass, density and speed of the dust grain, respectively.
are the mass, density and speed of the dust grain, respectively.
The electrostatic potential is obtained from the Poisson equation
The generation of the ionic drag force $\boldsymbol {F}_{{\rm id}}$![]() results from the acceleration of the ions under the influence of the sheath electrical potential. This force is a compass of two composites, that of collection $\boldsymbol {F}_{{\rm id}}^{{\rm coll}}$
results from the acceleration of the ions under the influence of the sheath electrical potential. This force is a compass of two composites, that of collection $\boldsymbol {F}_{{\rm id}}^{{\rm coll}}$![]() and of Coulomb $\boldsymbol {F}_{{\rm id}}^{{rm coul}}$
and of Coulomb $\boldsymbol {F}_{{\rm id}}^{{rm coul}}$![]() , which are given by (Shukla & Mamun Reference Shukla and Mamun2015)
, which are given by (Shukla & Mamun Reference Shukla and Mamun2015)
where $\tilde {v}_i=(v_i^2+8T_i/{\rm \pi} m_i)^{1/2}$![]() is the mean ion speed, $b_0={eq_d}/{m_iv_i^2}$
is the mean ion speed, $b_0={eq_d}/{m_iv_i^2}$![]() is the impact parameter for $90$
is the impact parameter for $90$![]() deflection and $b_c=r_d(1-{2eq_d}/{r_dm_iv_i^2})^{1/2}$
deflection and $b_c=r_d(1-{2eq_d}/{r_dm_iv_i^2})^{1/2}$![]() is the impact parameter for direct collision.
is the impact parameter for direct collision.
The neutral drag force $\boldsymbol {F}_{{\rm nd}}$![]() is given by the Epstein expression:
is given by the Epstein expression:
where $v_{n,th}=\sqrt {{8T_n}/{{\rm \pi} m_n}}$![]() is the neutral thermal velocity defined by the neutral gas temperature $T_n$
is the neutral thermal velocity defined by the neutral gas temperature $T_n$![]() and mass $m_n$
and mass $m_n$![]() .
.
In this paper, we assume that dust–dust interactions are negligible, which is reasonable given the weak density range we are considering. To explain the neglect of dust–plasma interactions, we note that the frequency of electron–dust and ion–dust collisions is proportional to the dust number density. For the dust density range with micro-sized dust grains considered here, and since we have a weakly ionised plasma, it can be shown that both dust–charged particles collisions and dust–neutral collisions are weak. Therefore, we assume that the dominant forces acting on the dust grains in the sheath are electric, gravitational, magnetic and drag forces.
In this work, we consider the Furman and Pivi (F-P) emission model (Furman & Pivi Reference Furman and Pivi2002) with all three types of secondary electrons mentioned above. Therefore, the secondary yield which corresponds to the ratio of the emitted current over the incident current can be written as follows:
where $\gamma _{e}(E_0)$![]() , $\gamma _{r}(E_0)$
, $\gamma _{r}(E_0)$![]() and $\gamma _{ts}(E_0)$
and $\gamma _{ts}(E_0)$![]() are the BEE, IRE and TEE yield, respectively.
are the BEE, IRE and TEE yield, respectively.
Furman & Pivi (Reference Furman and Pivi2002) provide formulae for $\gamma _{e}(E_0)$![]() and $\gamma _{r}(E_0)$
and $\gamma _{r}(E_0)$![]() as functions of incident electron energy $E_0$
as functions of incident electron energy $E_0$![]() . The formulae are as follows:
. The formulae are as follows:
where $P_{1,e}(\infty )$![]() is the yield of backscattered electrons for large primary electron energy ($E_0\rightarrow \infty$
is the yield of backscattered electrons for large primary electron energy ($E_0\rightarrow \infty$![]() ), $P_{1,e}$
), $P_{1,e}$![]() is the maximum backward electron emission yield, $E_e$
is the maximum backward electron emission yield, $E_e$![]() is the backscattered electron energy, $P_{1,r}(\infty )$
is the backscattered electron energy, $P_{1,r}(\infty )$![]() is the yield of reflected electron for primary electron energy ($E_0\rightarrow \infty$
is the yield of reflected electron for primary electron energy ($E_0\rightarrow \infty$![]() ), $W_f$
), $W_f$![]() is the work function related to the material, $E_r$
is the work function related to the material, $E_r$![]() is the reflected (IRE) electron energy, and $p$
is the reflected (IRE) electron energy, and $p$![]() and $r$
and $r$![]() are two dimensionless parameters.
are two dimensionless parameters.
The TEE yield can be determined by the Young–Dekker model (Young Reference Young1957):
where $\gamma _{m}$![]() is the maximum value of the TEE yield and $A={1}/{1-{\rm e}^{-b}}$
is the maximum value of the TEE yield and $A={1}/{1-{\rm e}^{-b}}$![]() , $y={E_0}/{E_{m}}$
, $y={E_0}/{E_{m}}$![]() and $n={(\mathrm {e}^{-b}-1)}/{(\mathrm {e}^{-b}(b+1)-1)}$
and $n={(\mathrm {e}^{-b}-1)}/{(\mathrm {e}^{-b}(b+1)-1)}$![]() , as well as $b$
, as well as $b$![]() is the unique solution of the transcendental equation $x=[1-({1}/{n})][\mathrm {e}^{x}-1]$
is the unique solution of the transcendental equation $x=[1-({1}/{n})][\mathrm {e}^{x}-1]$![]() .
.
All of the coefficients and parameters mentioned above have been determined by fitting the experimental data (Bronstein & Fraiman Reference Bronstein and Fraiman1969; Walker et al. Reference Walker, El Gomati, Assa'd and Zadrazil2008; Tolias Reference Tolias2014).
The dust charge arises from plasma currents due to the primary electrons and the ions reaching the dust grain surface. In this case, the dust charge is determined self-consistently by the charge conservation:
where $I_i$![]() , $I_e$
, $I_e$![]() and $I_s$
and $I_s$![]() are the plasma ion, primary electron and secondary electron currents, respectively. The charging of the dust can be considered as a local phenomenon (Barkan, Merlino & Dangelo Reference Barkan, Merlino and Dangelo1995). We write then,
are the plasma ion, primary electron and secondary electron currents, respectively. The charging of the dust can be considered as a local phenomenon (Barkan, Merlino & Dangelo Reference Barkan, Merlino and Dangelo1995). We write then,
According to the orbital motion limited (OML) theory, the expressions of the electron and the ion currents are given by (Gong & Du Reference Gong and Du2012; Shukla & Mamun Reference Shukla and Mamun2015; Ou & Long Reference Ou and Long2023)

for $q_d<0$![]() and
and

where $T_{se}$![]() is the temperature of secondary electrons. Here, $\mathbb {Z}_q^-$
is the temperature of secondary electrons. Here, $\mathbb {Z}_q^-$![]() and $\mathbb {Z}_q^+$
and $\mathbb {Z}_q^+$![]() are the two nonlinear core functions which are expressed as follows:
are the two nonlinear core functions which are expressed as follows:

where $Q_d={eq_d}/{r_dT_e}$![]() and
and


The OML theory can be applicable to calculate the dust charge if we use magnetic field intensity $B< B_{cr}(T)=({4.137}/{r_d(\mu m)})\sqrt {{T({\rm eV})}/{3({\rm eV})}}$![]() and the following condition $r_d<<\lambda _D<< l_{{\rm mfp}}$
and the following condition $r_d<<\lambda _D<< l_{{\rm mfp}}$![]() must be satisfied, where the electron Debye length in magnetised plasma with non-extensive electrons is given by (Hatami, Tribeche & Mamun Reference Hatami, Tribeche and Mamun2018)
must be satisfied, where the electron Debye length in magnetised plasma with non-extensive electrons is given by (Hatami, Tribeche & Mamun Reference Hatami, Tribeche and Mamun2018)

and $l_{{\rm mfp}}$![]() is the collision mean free path.
is the collision mean free path.
Additionally, to accurately describe dust particle dynamics using a continuous fluid model and a dust particle charge model based on OML theory, the dust density should be within the specified range $\lambda _{De}^{-3}< n_d<\lambda _{Di}^{-3}$![]() .
.
By replacing both (2.19) and (2.20) in (2.18), the normalised dust charge $Q_d={eq_d}/{r_dT_e}$![]() can be calculated from
can be calculated from
for $Q_d<0$![]() and
and
for $Q_d>0$![]() , where $\beta =({8m_i}/{{\rm \pi} m_e})^{{1}/{2}}$
, where $\beta =({8m_i}/{{\rm \pi} m_e})^{{1}/{2}}$![]() and $T_{se}={T_s}/{T_e}$
and $T_{se}={T_s}/{T_e}$![]() .
.
Each physical magnitude is adequately normalised,
$N_e=n_e/n_{e0}$![]() , $N_i=n_i/n_{i0}$
, $N_i=n_i/n_{i0}$![]() , $N_d=n_d/n_{d0}$
, $N_d=n_d/n_{d0}$![]() , $\xi =x/\lambda _D$
, $\xi =x/\lambda _D$![]() , $u_{ix}=v_{ix}/c_i$
, $u_{ix}=v_{ix}/c_i$![]() , $u_{{\rm d}x}=v_{{\rm d}x}/c_d$
, $u_{{\rm d}x}=v_{{\rm d}x}/c_d$![]() , $\eta =e\phi /T_e$
, $\eta =e\phi /T_e$![]() ,
,
where $c_i$![]() , $c_d$
, $c_d$![]() are the positive ion sound speed and the dust-acoustic speed, respectively.
are the positive ion sound speed and the dust-acoustic speed, respectively.
By substituting the above dimensionless variables into (2.4)–(2.9), we obtain
where $\mu ={e\lambda _DB}/{\sqrt {m_iT_e}}$![]() ; $\mu '=\mu \sqrt {{Z_dm_i}/{m_d}}$
; $\mu '=\mu \sqrt {{Z_dm_i}/{m_d}}$![]() $(Z_d={r_dT_e}/{e^2})$
$(Z_d={r_dT_e}/{e^2})$![]() ; $\varLambda ={\lambda _D}/{m_dc_d^2}$
; $\varLambda ={\lambda _D}/{m_dc_d^2}$![]() ; $\alpha ={2}/ {(3q-1)}$
; $\alpha ={2}/ {(3q-1)}$![]() ; $\delta ={n_{i0}}/{n_{e0}}$
; $\delta ={n_{i0}}/{n_{e0}}$![]() ; $Q_{d0}=Q_d(\phi =0)$
; $Q_{d0}=Q_d(\phi =0)$![]() ; $f_g={g\lambda _D}/{c_d^2}$
; $f_g={g\lambda _D}/{c_d^2}$![]() ; and $M_i$
; and $M_i$![]() and $M_d$
and $M_d$![]() are the ion Mach number and the dust Mach number, respectively.
are the ion Mach number and the dust Mach number, respectively.
To solve numerically the above differential equations, we consider the initial conditions at the sheath edge $(\xi =0)$![]() in which the electric potential is assumed to be zero $\phi (\xi =0)=0$
in which the electric potential is assumed to be zero $\phi (\xi =0)=0$![]() and the other conditions are as follows: $u_i(\xi =0)=M_i$
and the other conditions are as follows: $u_i(\xi =0)=M_i$![]() ; $u_{{\rm d}x}(\xi =0)=M_d$
; $u_{{\rm d}x}(\xi =0)=M_d$![]() ; and $u_{{\rm d}y}(\xi =0)=u_{{\rm d} z}(\xi =0)=0$
; and $u_{{\rm d}y}(\xi =0)=u_{{\rm d} z}(\xi =0)=0$![]() . In our calculation, the position of the wall is located when the electrons vanish and their density $n_{ew}$
. In our calculation, the position of the wall is located when the electrons vanish and their density $n_{ew}$![]() at the wall satisfies the following condition: $n_{ew}/n_{e0}\leq \epsilon$
at the wall satisfies the following condition: $n_{ew}/n_{e0}\leq \epsilon$![]() (where $\epsilon =10^{-4}$
(where $\epsilon =10^{-4}$![]() ).
).
To investigate the effect of SEE by the F-P model on the sheath structure, we depict the characteristics of the sheath using this model, which considers three types of secondary electron emissions (BEE, IRE and TEE). We compare these characteristics to those of the Sternglass model (Sternglass Reference Sternglass1957), which overlooks BEE and IRE, and to a model that does not account for any SEE (without SEE). In the following, we refer to the Sternglass model as the S-model.
The system of differential equations (2.27)–(2.36) is solved using the Runge–Kutta method of the fourth order, while (2.25) and (2.26) are calculated by the Newton–Raphson method. The Simpson method is used to solve numerically the integrals of the secondary electron current.
3 Numerical results and discussion
For numerical simulations, the default parameters are chosen as follows:
$n_n=5.10^{15}\,{\rm cm}^{-3}$![]() , $n_{e0}=10^{9}\,{\rm cm}^{-3}$
, $n_{e0}=10^{9}\,{\rm cm}^{-3}$![]() , $T_e=4\,{\rm eV}$
, $T_e=4\,{\rm eV}$![]() , $T_i=0.05\,{\rm eV}$
, $T_i=0.05\,{\rm eV}$![]() , $M_i=1.5$
, $M_i=1.5$![]() , $M_d=2$
, $M_d=2$![]() , $\delta =1.5$
, $\delta =1.5$![]() , $T_{se}=1.5$
, $T_{se}=1.5$![]() and $|\partial \eta /\partial \xi (\xi =0)|=0.01$
and $|\partial \eta /\partial \xi (\xi =0)|=0.01$![]() as boundary conditions at the plasma–sheath interface.
as boundary conditions at the plasma–sheath interface.
In this work, argon is considered to be the background gas. In addition, spherical dust particles of radius $r_d=2\,\mathrm {\mu } {\rm m}$![]() and mass density $\rho _d=19.3\,{\rm g}\,{\rm cm}^{-3}$
and mass density $\rho _d=19.3\,{\rm g}\,{\rm cm}^{-3}$![]() , typical of tungsten grains, are considered here.
, typical of tungsten grains, are considered here.
The secondary emission parameters are: $E_m=600\,$![]() eV, $\gamma _m=0.927$
eV, $\gamma _m=0.927$![]() , $P_{1,e}(\infty )=0.02$
, $P_{1,e}(\infty )=0.02$![]() , $P_{1,e}=0.1705$
, $P_{1,e}=0.1705$![]() , $E_e=13.14\,{\rm eV}$
, $E_e=13.14\,{\rm eV}$![]() , $W_f=9.657\,{\rm eV}$
, $W_f=9.657\,{\rm eV}$![]() , $p=1.7$
, $p=1.7$![]() , $P_{1,r}(\infty )=0.46$
, $P_{1,r}(\infty )=0.46$![]() , $E_r=23.36\,{\rm eV}$
, $E_r=23.36\,{\rm eV}$![]() , $r=1.5$
, $r=1.5$![]() , $b=2.1934$
, $b=2.1934$![]() and $A=1.1255$
and $A=1.1255$![]() .
.
The selection of the dust grain's Mach number is based on the Böhm criterion for sheath formation. Furthermore, to avoid a singularity at the sheath edge, a small non-zero electric field is assumed there. For the sheath to form at a finite distance, the electric field at the sheath edge must have a small finite value.
Before discussing the numerical results, we evaluate the suitability of the orbital motion limited (OML) theory and the continuous fluid model for dust particles. Therefore, based on the parameters listed above, the dust density falls within the range $9.04\times 10^3< n_d<1.26\times 10^7$![]() (in ${\rm cm}^{-3}$
(in ${\rm cm}^{-3}$![]() ), which aligns with the assumption made in this study.
), which aligns with the assumption made in this study.
Figures 2(a)–2(c) show the profiles of the sheath potential as functions of $x$![]() for three different values of $q$
for three different values of $q$![]() . Each of these three cases corresponds to three models of SEE: F-P model, S-model and without SEE. These three figures demonstrate how the normalised electric potential in a sheath decreases as the non-extensive parameter $q$
. Each of these three cases corresponds to three models of SEE: F-P model, S-model and without SEE. These three figures demonstrate how the normalised electric potential in a sheath decreases as the non-extensive parameter $q$![]() increases. This potential is inversely related to the distance from the sheath edge to the wall; the further one moves away from the edge and closer to the wall, the greater the absolute value of the potential. Figure 2(a) compares two scenarios of secondary electron emission; one using a Sternglass model (S-model) and the other employing an F-P model. It is observed that the F-P model predicts a higher absolute value of the normalised potential than the S-model across the range of $q$
increases. This potential is inversely related to the distance from the sheath edge to the wall; the further one moves away from the edge and closer to the wall, the greater the absolute value of the potential. Figure 2(a) compares two scenarios of secondary electron emission; one using a Sternglass model (S-model) and the other employing an F-P model. It is observed that the F-P model predicts a higher absolute value of the normalised potential than the S-model across the range of $q$![]() values. Additionally, the difference between the models becomes more pronounced at lower $q$
values. Additionally, the difference between the models becomes more pronounced at lower $q$![]() values (see figure 2c). This suggests that the influence of the non-extensive parameter $q$
values (see figure 2c). This suggests that the influence of the non-extensive parameter $q$![]() on the electric potential is more significant in the F-P model, highlighting the sensitivity of the sheath's electrical characteristics to the choice of the electron emission model, especially at lower $q$
on the electric potential is more significant in the F-P model, highlighting the sensitivity of the sheath's electrical characteristics to the choice of the electron emission model, especially at lower $q$![]() values.
values.

Figure 2. Normalised potential sheath profiles: (a) at $q=0.95$![]() ; (b) at $q=0.9$
; (b) at $q=0.9$![]() ; (c) at $q=0.85$
; (c) at $q=0.85$![]() .
.
Using the same non-extensive parameter $q$![]() values as in figure 2, figure 3 illustrates the spatial distributions of dust charge in the sheath when accounting for secondary electron emission through both the S-model and the F-P model. Figure 3(a) delineates that the absolute value of the dust charge diminishes progressively until it reaches an inversion point. Beyond this point, the dust charge rapidly increases when nearing the wall. The presence of secondary electrons in the F-P model causes the dust charge to become less negative, transitioning more swiftly to a positive charge. This suggests a significant influence of the secondary electron emission accounted for in the F-P model on the charging dynamics of dust in the sheath, especially in the proximity of the wall where these effects become more marked.
values as in figure 2, figure 3 illustrates the spatial distributions of dust charge in the sheath when accounting for secondary electron emission through both the S-model and the F-P model. Figure 3(a) delineates that the absolute value of the dust charge diminishes progressively until it reaches an inversion point. Beyond this point, the dust charge rapidly increases when nearing the wall. The presence of secondary electrons in the F-P model causes the dust charge to become less negative, transitioning more swiftly to a positive charge. This suggests a significant influence of the secondary electron emission accounted for in the F-P model on the charging dynamics of dust in the sheath, especially in the proximity of the wall where these effects become more marked.

Figure 3. Evolution of the normalised dust charge under three values of $q$![]() : (a) at $q=0.95$
: (a) at $q=0.95$![]() ; (b) at $q=0.9$
; (b) at $q=0.9$![]() ; (c) at $q=0.85$
; (c) at $q=0.85$![]() .
.
The observed results can be interpreted as follows. The F-P model incorporates electron emissions through mechanisms such as backscattering, inelastic reflection and true secondary emissions, which significantly contribute to the emission of secondary electrons. These secondary electrons generate a positive current at the surface of dust grains within the sheath, effectively rendering the dust charge less negative. In particular, when the value of $q$![]() is $0.95$
is $0.95$![]() , corresponding to the presence of less energetic electrons, the contribution of true secondary emissions seems less significant compared with the other two contributions. However, at lower $q$
, corresponding to the presence of less energetic electrons, the contribution of true secondary emissions seems less significant compared with the other two contributions. However, at lower $q$![]() values that correspond to the presence of more energetic electrons, true secondary emissions become increasingly important alongside backscattered electrons (BEE) and inelastic-reflected electrons (IRE). This suggests that the F-P model does accurately capture secondary electron emissions under these conditions, as it clearly modifies the charge distribution in the sheath.
values that correspond to the presence of more energetic electrons, true secondary emissions become increasingly important alongside backscattered electrons (BEE) and inelastic-reflected electrons (IRE). This suggests that the F-P model does accurately capture secondary electron emissions under these conditions, as it clearly modifies the charge distribution in the sheath.
In the F-P model, the accumulated dust grains carry a reduced negative charge. This reduction amplifies the absolute value of the electrical potential within the sheath. Beyond the inversion point of dust charge, where electron depletion is substantial, dust particles begin to accrue positive ions, which are abundant in this region close to the wall. As a result, the positive charge on the dust escalates rapidly and intensifies near the wall. Additionally, the influence of the F-P model becomes more distinct near the wall where the value of $Q_d$![]() is diminished at a given value of $q$
is diminished at a given value of $q$![]() . It is thus inferred that the dust charge is a pivotal factor in determining the characteristics of the sheath potential.
. It is thus inferred that the dust charge is a pivotal factor in determining the characteristics of the sheath potential.
Figure 4 illustrates the sheath width as a function of the non-extensive parameter $q$![]() , comparing three scenarios: one with SEE using the S-model, another with SEE using the F-P model, and a third without SEE. As the value of $q$
, comparing three scenarios: one with SEE using the S-model, another with SEE using the F-P model, and a third without SEE. As the value of $q$![]() decreases, the sheath width exhibits distinct responses for each scenario. With the S-model, the sheath width increases significantly. In contrast, with the F-P model, the sheath width exhibits a more modest expansion. Additionally, without SEE, the behaviour of the sheath width would likely differ from the two scenarios with SEE. The variation in sheath width across these scenarios can be attributed to the differing impacts of the electric potential, which is more pronounced in the F-P model. The amplification of the electric potential in the F-P model may accelerate electron depletion, which could, counterintuitively, lead to a reduction in sheath width.
decreases, the sheath width exhibits distinct responses for each scenario. With the S-model, the sheath width increases significantly. In contrast, with the F-P model, the sheath width exhibits a more modest expansion. Additionally, without SEE, the behaviour of the sheath width would likely differ from the two scenarios with SEE. The variation in sheath width across these scenarios can be attributed to the differing impacts of the electric potential, which is more pronounced in the F-P model. The amplification of the electric potential in the F-P model may accelerate electron depletion, which could, counterintuitively, lead to a reduction in sheath width.

Figure 4. Profiles of the sheath width as function of $q$![]() with F-P model (pointed), S-model (dashed) and without SEE (solid).
with F-P model (pointed), S-model (dashed) and without SEE (solid).
We have seen above that secondary emission electrons have a clearer impact on potential sheath and dust charge using the F-P model than the S-model. For this reason, in the following, we will discuss the other characteristics of the sheath using only these two models for three values of $q$![]() .
.
According to figure 5, which depicts the variation of the normalised electron density along the sheath axis ($x$![]() ) using both the Sternglass and the F-P models, it is observed that the electron density decreases more rapidly when the F-P model is applied. This phenomenon can be attributed to the stronger electron repulsion under the influence of the intensified electric force within the F-P model. Thus, this leads to a notably sharper decline in electron density when the F-P model is employed.
) using both the Sternglass and the F-P models, it is observed that the electron density decreases more rapidly when the F-P model is applied. This phenomenon can be attributed to the stronger electron repulsion under the influence of the intensified electric force within the F-P model. Thus, this leads to a notably sharper decline in electron density when the F-P model is employed.

Figure 5. Normalised electron density under three values of $q$![]() with S-model (solid) and F-P model (dashed) of SEE.
with S-model (solid) and F-P model (dashed) of SEE.
Figure 6 illustrates the variation in normalised ion velocity ($U_{ix}$![]() ) with distance ($x$
) with distance ($x$![]() ) in the sheath region, affected by different non-extensive parameters $q$
) in the sheath region, affected by different non-extensive parameters $q$![]() . This figure compares the Sternglass model (S-model) of secondary electron emission and that of the F-P model. In both models, ion velocity increases as the distance from the sheath edge grows, signifying ion acceleration towards the wall. Notably, the ion velocity in the F-P model is higher than in the Sternglass SEE model for the same $q$
. This figure compares the Sternglass model (S-model) of secondary electron emission and that of the F-P model. In both models, ion velocity increases as the distance from the sheath edge grows, signifying ion acceleration towards the wall. Notably, the ion velocity in the F-P model is higher than in the Sternglass SEE model for the same $q$![]() value. This disparity is especially evident for lower $q$
value. This disparity is especially evident for lower $q$![]() values, where the SEE with F-P model shows a significant increase in ion velocity near the wall. The differences between these models highlight the F-P model's inclination to forecast more pronounced ion acceleration due to the enhanced electric potential from secondary electron emission. Furthermore, the increasing differences in ion velocities for various $q$
values, where the SEE with F-P model shows a significant increase in ion velocity near the wall. The differences between these models highlight the F-P model's inclination to forecast more pronounced ion acceleration due to the enhanced electric potential from secondary electron emission. Furthermore, the increasing differences in ion velocities for various $q$![]() values in the F-P model suggest a greater sensitivity to changes in the non-extensive parameter. Overall, this depiction underscores the impact of the chosen electron emission model and the non-extensive parameter $q$
values in the F-P model suggest a greater sensitivity to changes in the non-extensive parameter. Overall, this depiction underscores the impact of the chosen electron emission model and the non-extensive parameter $q$![]() on ion velocity in the sheath, shedding light on the complex dynamics of electric fields and ion motion in plasma.
on ion velocity in the sheath, shedding light on the complex dynamics of electric fields and ion motion in plasma.

Figure 6. Profiles of the normalised ion velocity in the sheath under three values of $q$![]() with S-model (solid) and F-P model (dashed) of SEE.
with S-model (solid) and F-P model (dashed) of SEE.
Figure 7 delineates the influence of SEE as characterised by the F-P model and S-model on the spatial distribution of dust particle velocity within the sheath. The normalised velocity of the dust particles is shown to decrease marginally with the application of the F-P model, with this effect intensifying closer to the wall. This is attributed to the F-P model's role in heightening the absolute value of the electric potential, which in turn exerts a stronger electrostatic force on negatively charged dust grains, diminishing their velocity. It is important to note the inverse relationship between velocity in the depth direction and the dust density as described by (2.28) and (2.29), which suggests that these velocity trends can be correlated to dust density, although the density curves are not presented.

Figure 7. Evolution of dust velocity into the sheath as a function of $q$![]() with (a) S-model and (b) F-P model of SEE.
with (a) S-model and (b) F-P model of SEE.
The stratification of dust within the sheath is the result of a delicate balance between downward forces such as gravity and ion drag, and upward forces such as the electrostatic force and, to a lesser extent, neutral drag. Near the edge of the sheath, the electrostatic force is relatively weak, allowing gravity and ion drag to dominate and accelerate the dust grains. As the distance from the sheath edge increases, the electrostatic force becomes more significant, hastening the dust particles and causing them to accumulate at certain points within the sheath.
The accumulation of these dust grains creates a local negative potential, which in turn dampens the impact of the electrostatic force on subsequent dust particles. As a consequence, these negatively charged particles begin accelerating again towards the wall. This cyclical process leads to an increase in the number of dust grains levitating in the plasma sheath until such time as the dust charge turns positive. Near the wall, due to the substantial depletion of electrons, dust particles cannot maintain a negative charge and beyond this inversion point, positively charged dust particles are no longer propelled by the electrostatic force and ultimately settle on the wall, capping the quantity of levitating dust. At lower values of $q$![]() , the dynamics of dust particles are profoundly influenced by secondary electron emission, as modelled by the F-P model, particularly due to its significant effect on the sheath potential. The complex interplay of forces and local electric fields governs the movement and distribution of dust particles, reflecting the intricate nature of plasma–sheath interactions.
, the dynamics of dust particles are profoundly influenced by secondary electron emission, as modelled by the F-P model, particularly due to its significant effect on the sheath potential. The complex interplay of forces and local electric fields governs the movement and distribution of dust particles, reflecting the intricate nature of plasma–sheath interactions.
4 Conclusion
In this study, a detailed analysis is presented on the impact of secondary electron emission on the characteristics of a dusty plasma sheath, emphasising the role of non-extensive electrons. Using the F-P model, which incorporates electron emission through backscattering, inelastic reflection and true secondary emission, it is shown that secondary electron emission significantly modifies the properties of the plasma sheath. Notable findings include an increase in the absolute value of the electrostatic potential and a decrease in electron density, resulting in a narrower sheath. Additionally, this work compares the efficacy of the F-P model with that of the Sternglass emission model. It reveals that the choice of electron emission model greatly affects various sheath parameters, such as dust particle charge dynamics, sheath width, and the velocities of dust particles and ions. The F-P model displays more pronounced effects compared with the S-model, underlining a complex interplay of forces and local electric fields that influence the movement and distribution of dust particles. The study concludes that the effects of secondary electron emission, particularly from backscattered, inelastically reflected electrons and true secondary emission are crucial elements in the dynamics of dusty plasma sheaths, especially when considering superextensive electrons.
Acknowledgements
Editor Edward Thomas, Jr. thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.