Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-05T07:53:46.495Z Has data issue: false hasContentIssue false
  • English
  • Français

Study of intrinsic rotation by the Gyrokinetic Electromagnetic Numerical Experiment code in the Joint Texas Experimental Tokamak

Part of: Focus on Fusion

Published online by Cambridge University Press:  11 May 2020

Duoqin Wang ,
Wei Yan Open the ORCID record for Wei Yan [Opens in a new window] ,
Zhongyong Chen ,
Xin Ye ,
Wei Li ,
Zhiyang Yin ,
Jie Hu ,
Wei Bai ,
Yu Zhong  and
J-TEXT Team
Duoqin Wang
Affiliation:
International Joint Research Laboratory of Magnetic Confinement Fusion and Plasma Physics, State Key Laboratory of Advanced Electromagnetic Engineering and Technology, School of Electrical and Electronic Engineering, Huazhong University of Science and Technology, Wuhan430074, People’s Republic of China
Wei Yan*
Affiliation:
International Joint Research Laboratory of Magnetic Confinement Fusion and Plasma Physics, State Key Laboratory of Advanced Electromagnetic Engineering and Technology, School of Electrical and Electronic Engineering, Huazhong University of Science and Technology, Wuhan430074, People’s Republic of China
Zhongyong Chen
Affiliation:
International Joint Research Laboratory of Magnetic Confinement Fusion and Plasma Physics, State Key Laboratory of Advanced Electromagnetic Engineering and Technology, School of Electrical and Electronic Engineering, Huazhong University of Science and Technology, Wuhan430074, People’s Republic of China Chengdu University, 610106, Chengdu, People’s Republic of China
Xin Ye
Affiliation:
International Joint Research Laboratory of Magnetic Confinement Fusion and Plasma Physics, State Key Laboratory of Advanced Electromagnetic Engineering and Technology, School of Electrical and Electronic Engineering, Huazhong University of Science and Technology, Wuhan430074, People’s Republic of China
Wei Li
Affiliation:
International Joint Research Laboratory of Magnetic Confinement Fusion and Plasma Physics, State Key Laboratory of Advanced Electromagnetic Engineering and Technology, School of Electrical and Electronic Engineering, Huazhong University of Science and Technology, Wuhan430074, People’s Republic of China
Zhiyang Yin
Affiliation:
International Joint Research Laboratory of Magnetic Confinement Fusion and Plasma Physics, State Key Laboratory of Advanced Electromagnetic Engineering and Technology, School of Electrical and Electronic Engineering, Huazhong University of Science and Technology, Wuhan430074, People’s Republic of China
Jie Hu
Affiliation:
International Joint Research Laboratory of Magnetic Confinement Fusion and Plasma Physics, State Key Laboratory of Advanced Electromagnetic Engineering and Technology, School of Electrical and Electronic Engineering, Huazhong University of Science and Technology, Wuhan430074, People’s Republic of China
Wei Bai
Affiliation:
International Joint Research Laboratory of Magnetic Confinement Fusion and Plasma Physics, State Key Laboratory of Advanced Electromagnetic Engineering and Technology, School of Electrical and Electronic Engineering, Huazhong University of Science and Technology, Wuhan430074, People’s Republic of China
Yu Zhong
Affiliation:
International Joint Research Laboratory of Magnetic Confinement Fusion and Plasma Physics, State Key Laboratory of Advanced Electromagnetic Engineering and Technology, School of Electrical and Electronic Engineering, Huazhong University of Science and Technology, Wuhan430074, People’s Republic of China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The core toroidal plasma intrinsic rotation has been studied by experiments and simulations in the Joint Texas Experimental Tokamak (J-TEXT). The direction of core intrinsic rotation in the J-TEXT plasma is counter-current. As the plasma density ramps up, the rotation velocity increases in the counter-current direction. By comparing four different electron densities, linear local gyrokinetic simulations have been performed by the Gyrokinetic Electromagnetic Numerical Experiment code for the first time on J-TEXT. It is found that the most dominant turbulence is the ion temperature gradient at 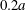$0.2a$, where $a$ is the minor radius of the plasma and this is unchanged during the plasma density ramp up. By scanning the radial wave vectors, it is found that the residual stress term reverses from negative to positive when the plasma density exceeds a certain threshold. The pinch term is larger than the residual stress term at all four electron densities, which means that the pinch term is always dominant in the core of a J-TEXT plasma.

Keywords

fusion plasmaplasma flowsplasma simulation
Type
Research Article
Information
Journal of Plasma Physics , Volume 86 , Issue 3 , June 2020 , 815860301
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

See the author list of Liang et al. (2019)

References

Angioni, C., Camenen, Y., Casson, F. J., Fable, E., McDermott, R. M., Peeters, A. G. & Rice, J. E. 2012 Off-diagonal particle and toroidal momentum transport: a survey of experimental, theoretical and modelling aspects. Nucl. Fusion 52 (11), 114003.CrossRefGoogle Scholar
Angioni, C. et al. 2017 A comprehensive study on rotation reversal in KSTAR: experimental observations and modelling. Nucl. Fusion 57 (12), 126008.Google Scholar
Barnes, M., Parra, F. I., Lee, J. P., Belli, E. A., Nave, M. F. F. & White, A. E. 2013 Intrinsic rotation driven by non-Maxwellian equilibria in Tokamak plasmas. Phys. Rev. Lett. 111 (5), 55005.CrossRefGoogle ScholarPubMed
Bernardo, J. et al. 2015 Density impact on toroidal rotation in Tore Supra: experimental observations and theoretical investigation. Plasma Phys. Control. Fusion 57 (3), 35002.CrossRefGoogle Scholar
Bondeson, A. & Ward, D. J. 1994 Stabilization of external modes in tokamaks by resistive walls and plasma rotation. Phys. Rev. Lett. 72 (17), 2709–2712.CrossRefGoogle ScholarPubMed
Buchholz, R., Grosshauser, S. R., Hornsby, W. A., Migliano, P., Peeters, A. G., Camenen, Y. & Casson, F. J. 2014 Toroidal momentum transport in a tokamak due to profile shearing. Phys. Plasmas 12 (6), 62304.CrossRefGoogle Scholar
Burrell, K. H. et al. 1994 Role of the radial electric field in the transition from L (low) mode to H (high) mode to VH (very high) mode in the DIII-D tokamak*. Phys. Plasmas 1 (5), 1536–1544.CrossRefGoogle Scholar
Camenen, Y., Peeters, A. G., Angioni, C., Casson, F. J. & Hornsby, W. A. 2009 Transport of parallel momentum induced by current-symmetry breaking in toroidal plasmas. Phys. Rev. Lett. 102 (12), 125001.CrossRefGoogle ScholarPubMed
Camenen, Y., Idomura, Y., Jolliet, S. & Peeters, A. G. 2011 Consequences of profile shearing on toroidal momentum transport. Nucl. Fusion 51 (7), 73039.CrossRefGoogle Scholar
Carraro, L., Pol, G. D., Puiatti, M. E., Sattin, F., Scarin, P. & Valisa, M. 2000 Edge temperature and density measurements with a thermal helium beam in the RFX reversed field pinch. Plasma Phys. Control. Fusion 42 (1), 1–14.CrossRefGoogle Scholar
Casson, F. J., Peeters, A. G., Camenen, Y., Hornsby, W. A. & Snodin, A. P. 2009 Anomalous parallel momentum transport due to E$\times$B flow shear in a tokamak plasma. Phys. Plasmas 16 (9), 92303.CrossRefGoogle Scholar
Connor, J. W., Hastie, R. J. & Taylor, J. B. 1979 High mode number stability of an axisymmetric toroidal plasma. Proc. R. Soc. Lond. A 365 (1720), 1–17.Google Scholar
Dannert, T. & Jenko, F. 2005 Gyrokinetic simulation of collisionless trapped-electron mode turbulence. Phys. Plasmas 12 (7), 72309.CrossRefGoogle Scholar
Dewar, R. L. & Glasser, A. H. 1983 Ballooning mode spectrum in general toroidal systems. Phys. Fluids 26 (10), 3038–3052.CrossRefGoogle Scholar
Diamond, P. H. et al. 2013 An overview of intrinsic torque and momentum transport bifurcations in toroidal plasmas. Nucl. Fusion 53 (10), 104019.CrossRefGoogle Scholar
Diamond, P. H., McDevitt, C. J., Gürcan, Ö.D., Hahm, T. S. & Naulin, V. 2008 Transport of parallel momentum by collisionless drift wave turbulence. Phys. Plasmas 15 (1), 12303.CrossRefGoogle Scholar
Duval, B. P., Bortolon, A., Karpushov, A., Pitts, R. A., Pochelon, A., Sauter, O., Scarabosio, A., Turri, G.& the TCV team 2008 Spontaneous L-mode plasma rotation scaling in the TCV tokamak. Phys. Plasmas 15 (5), 56113.CrossRefGoogle Scholar
Duval, B. P., Bortolon, A., Karpushov, A., Pitts, R. A., Pochelon, A., Scarabosio, A.& the TCV team 2007 Bulk plasma rotation in the TCV tokamak in the absence of external momentum input. Plasma Phys. Control. Fusion 49 (12B), B195–B209.CrossRefGoogle Scholar
Garofalo, A. M. et al. 1999 Direct observation of the resistive wall mode in a tokamak and its interaction with plasma rotation. Phys. Rev. Lett. 82 (19), 3811–3814.CrossRefGoogle Scholar
GENE development team2018 The Gyrokinetic Plasma Turbulence Code Gene: User Manual.Google Scholar
Görler, T., Lapillonne, X., Brunner, S., Dannert, T., Jenko, F., Merz, F. & Told, D. 2011 The global version of the gyrokinetic turbulence code GENE. J. Comput. Phys. 230 (18), 7053–7071.CrossRefGoogle Scholar
Görler, T., Told, D., Jenko, F., Holland, C., Rhodes, T. L. & White, A. E. 2014 A flux-matched gyrokinetic analysis of DIII-D L-mode turbulence. Phys. Plasmas 21 (12), 122307.CrossRefGoogle Scholar
Gürcan, Ö. D., Diamond, P. H., Hennequin, P., McDevitt, C. J., Garbet, X. & Bourdelle, C. 2010 Residual parallel Reynolds stress due to turbulence intensity gradient in tokamak plasmas. Phys. Plasmas 17 (11), 112309.CrossRefGoogle Scholar
Hahm, T. S. & Burrell, K. H. 1995 Flow shear induced fluctuation suppression in finite aspect ratio shaped tokamak plasma. Phys. Plasmas 2 (5), 1648–1651.CrossRefGoogle Scholar
Hahm, T. S., Diamond, P. H., Gurcan, O. D. & Rewoldt, G. 2007 Nonlinear gyrokinetic theory of toroidal momentum pinch. Phys. Plasmas 14 (7), 72302.CrossRefGoogle Scholar
Hillesheim, J. C., Parra, F. I., Barnes, M., Crocker, N. A., Meyer, H., Peebles, W. A., Scannell, R., Thornton, A.& the MAST team 2015 Dependence of intrinsic rotation reversals on collisionality in MAST. Nucl. Fusion 55 (3), 32003.CrossRefGoogle Scholar
Hornsby, W. A., Angioni, C., Fable, E., Manas, P., McDermott, R., Peeters, A. G., Barnes, M., Parra, F.& the ASDEX Upgrade team 2017 On the effect of neoclassical flows on intrinsic momentum in ASDEX Upgrade Ohmic L-mode plasmas. Nucl. Fusion 57 (4), 46008.CrossRefGoogle Scholar
Hornsby, W. A., Angioni, C., Lu, Z. X., Fable, E., Erofeev, I., McDermott, R., Medvedeva, A., Lebschy, A., Peeters, A. G.& the ASDEX Upgrade team 2018 Global gyrokinetic simulations of intrinsic rotation in ASDEX Upgrade Ohmic L-mode plasmas. Nucl. Fusion 58 (5), 56008.CrossRefGoogle Scholar
Jenko, F., Dorland, W., Kotschenreuther, M. & Rogers, B. N. 2000 Electron temperature gradient driven turbulence. Phys. Plasmas 7 (5), 1904–1910.CrossRefGoogle Scholar
Jenko, F.& GENE development team 2019 The GENE code. URL http://genecode.org.Google Scholar
Lee, W. D., Rice, J. E., Marmar, E. S., Greenwald, M. J., Hutchinson, I. H. & Snipes, J. A. 2003 Observation of anomalous momentum transport in tokamak plasmas with no momentum input. Phys. Rev. Lett. 91 (20), 205003.CrossRefGoogle ScholarPubMed
Liang, Y. et al. 2019 Overview of the recent experimental research on the J-TEXT tokamak. Nucl. Fusion 59 (11), 112016.CrossRefGoogle Scholar
Liu, H., Chen, Z., Xu, Y., Zhu, L., Chen, Z., Zhuang, G.& the J-TEXT team 2018 Investigation of toroidal rotation modulation and momentum transport with electrode biasing in J-TEXT tokamak. Plasma Phys. Control. Fusion 60 (11), 115012.CrossRefGoogle Scholar
Lu, Z. X., Wang, W. X., Diamond, P. H., Tynan, G., Ethier, S., Gao, C. & Rice, J. 2015 Intrinsic torque reversals induced by magnetic shear effects on the turbulence spectrum in tokamak plasmas. Phys. Plasmas 22 (5), 55705.CrossRefGoogle Scholar
McDermott, R. M. et al. 2011 Core momentum and particle transport studies in the ASDEX Upgrade tokamak. Plasma Phys. Control. Fusion 53 (12), 124013.CrossRefGoogle Scholar
McDermott, R. M., Angioni, C., Conway, G. D., Dux, R., Fable, E., Fischer, R., Pütterich, T., Ryter, F., Viezzer, E.& the ASDEX Upgrade team 2014 Core intrinsic rotation behaviour in ASDEX Upgrade ohmic L-mode plasmas. Nucl. Fusion 54 (4), 43009.CrossRefGoogle Scholar
Na, D. H., Na, Y., Lee, S. G., Angioni, C. & Yang, S. M. 2016 Observation of the intrinsic rotation in KSTAR Ohmic L-mode plasmas. Nucl. Fusion 56 (3), 36011.CrossRefGoogle Scholar
Parra, F. I., Barnes, M. & Peeters, A. G. 2011 Up-down symmetry of the turbulent transport of toroidal angular momentum in tokamaks. Phys. Plasmas 18 (6), 62501.CrossRefGoogle Scholar
Peeters, A. G., Angioni, C. & Strintzi, D. 2007 Toroidal momentum pinch velocity due to the coriolis drift effect on small scale instabilities in a toroidal plasma. Phys. Rev. Lett. 98 (26), 265003.CrossRefGoogle Scholar
Peeters, A. G., Angioni, C., Camenen, Y., Casson, F. J. & Hornsby, W. A. 2009 The influence of the self-consistent mode structure on the Coriolis pinch effect. Phys. Plasmas 16 (6), 62311.CrossRefGoogle Scholar
Peeters, A. G. et al. 2011 Overview of toroidal momentum transport. Nucl. Fusion 51 (9), 94027.CrossRefGoogle Scholar
Rice, J. E. et al. 2004 Observations of anomalous momentum transport in Alcator C-Mod plasmas with no momentum input. Nucl. Fusion 44 (3), 379–386.CrossRefGoogle Scholar
Rice, J. E. et al. 2007 Inter-machine comparison of intrinsic toroidal rotation in tokamaks. Nucl. Fusion 47 (11), 1618–1624.CrossRefGoogle Scholar
Rice, J. E. et al. 2011a Edge temperature gradient as intrinsic rotation drive in Alcator C-Mod tokamak plasmas. Phys. Rev. Lett. 106 (21), 215001.CrossRefGoogle Scholar
Rice, J. E., Duval, B. P., Reinke, M. L., Podpaly, Y. A. & Bortolon, A. 2011b Observations of core toroidal rotation reversals in Alcator C-Mod ohmic L-mode plasmas. Nucl. Fusion 51 (8), 83005.CrossRefGoogle Scholar
Rice, J. E., Marmar, E. S., Bombarda, F. & Qu, L. 1997 X-ray observations of central toroidal rotation in ohmic Alcator C-Mod plasmas. Nucl. Fusion 37 (3), 421–426.CrossRefGoogle Scholar
Scarabosio, A., Bortolon, A., Duval, B. P., Karpushov, A. & Pochelon, A. 2006 Toroidal plasma rotation in the TCV tokamak. Plasma Phys. Control. Fusion 48 (5), 663–683.CrossRefGoogle Scholar
Shaing, K. C. & Crume, E. J. 1989 Bifurcation theory of poloidal rotation in tokamaks: a model for L-H transition. Phys. Rev. Lett. 63 (21), 2369–2372.CrossRefGoogle Scholar
Singh, R., Brunner, S., Ganesh, R. & Jenko, F. 2014 Finite ballooning angle effects on ion temperature gradient driven mode in gyrokinetic flux tube simulations. Phys. Plasmas 21 (3), 32115.CrossRefGoogle Scholar
Stoltzfus-Dueck, T. 2019 Intrinsic rotation in axisymmetric devices. Plasma Phys. Control. Fusion 61, 12400312.CrossRefGoogle Scholar
Sugama, H., Watanabe, T. H., Nunami, M. & Nishimura, S. 2011 Momentum balance and radial electric fields in axisymmetric and nonaxisymmetric toroidal plasmas. Plasma Phys. Control. Fusion 53 (2), 24004.CrossRefGoogle Scholar
Terry, P. W. 2000 Suppression of turbulence and transport by sheared flow. Rev. Mod. Phys. 72 (1), 109–165.CrossRefGoogle Scholar
Waltz, R. E., Staebler, G. M., Candy, J. & Hinton, F. L. 2007 Gyrokinetic theory and simulation of angular momentum transport. Phys. Plasmas 14 (12), 122507.CrossRefGoogle Scholar
Wang, L. & Diamond, P. H. 2013 Gyrokinetic theory of turbulent acceleration of parallel rotation in tokamak plasmas. Phys. Rev. Lett. 110 (26), 265006.CrossRefGoogle ScholarPubMed
Yan, W. et al. 2018 Response of plasma rotation to resonant magnetic perturbations in J-TEXT tokamak. Plasma Phys. Control. Fusion 60 (3), 35007.CrossRefGoogle Scholar
Yan, W., Chen, Z. Y., Jin, W., Huang, D. W., Ding, Y. H., Li, J. C., Zhang, X. Q., Lee, S. G., Shi, Y. J. & Zhuang, G. 2014 Wavelength calibration of x-ray imaging crystal spectrometer on Joint Texas Experimental Tokamak. Rev. Sci. Instrum. 85 (11), 11E–416E.CrossRefGoogle ScholarPubMed
Zhuang, G., Chen, J., Li, Q., Gao, L., Wang, Z. J., Liu, Y. & Chen, W. 2013 First results of the J-TEXT high-resolution 3-wave polarimeter-interferometer system. J. Instrum. 8 (10), C10019.CrossRefGoogle Scholar