Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-04-24T11:31:36.815Z Has data issue: true hasContentIssue false
  • English
  • Français

Quantized tensor networks for solving the Vlasov–Maxwell equations

Part of: Plasma and quantum information sciences

Published online by Cambridge University Press:  18 September 2024

Erika Ye Open the ORCID record for Erika Ye [Opens in a new window]  and
Nuno F. Loureiro Open the ORCID record for Nuno F. Loureiro [Opens in a new window]
Erika Ye*
Affiliation:
Applied Mathematics and Computational Research Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
Nuno F. Loureiro
Affiliation:
Plasma Science and Fusion Center, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The Vlasov–Maxwell equations provide an ab initio description of collisionless plasmas, but solving them is often impractical because of the wide range of spatial and temporal scales that must be resolved and the high dimensionality of the problem. In this work, we present a quantum-inspired semi-implicit Vlasov–Maxwell solver that uses the quantized tensor network (QTN) framework. With this QTN solver, the cost of grid-based numerical simulation of size $N$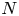 is reduced from $O(N)$ 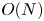to $O(\text {poly}(D))$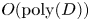, where $D$ 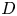is the ‘rank’ or ‘bond dimension’ of the QTN and is typically set to be much smaller than $N$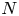. We find that for the five-dimensional test problems considered here, a modest $D=64$ appears to be sufficient for capturing the expected physics despite the simulations using a total of $N=2^{36}$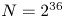 grid points, which would require $D=2^{18}$ 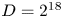for full-rank calculations. Additionally, we observe that a QTN time evolution scheme based on the Dirac–Frenkel variational principle allows one to use somewhat larger time steps than prescribed by the Courant–Friedrichs–Lewy constraint. As such, this work demonstrates that the QTN format is a promising means of approximately solving the Vlasov–Maxwell equations with significantly reduced cost.

Keywords

plasma simulationplasma dynamics
Type
Research Article
Information
Journal of Plasma Physics , Volume 90 , Issue 3 , June 2024 , 805900301
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Allmann-Rahn, F., Grauer, R. & Kormann, K. 2022 A parallel low-rank solver for the six-dimensional Vlasov-Maxwell equations. J. Comput. Phys. 469, 111562.Google Scholar
Birn, J. & Hesse, M. 2001 Geospace environment modeling (GEM) magnetic reconnection challenge: resistive tearing, anisotropic pressure and Hall effects. J. Geophys. Res. Space 106 (A3), 3737–3750.Google Scholar
Cappelli, L., Tacchino, F., Murante, G., Borgani, S. & Tavernelli, I 2024 From Vlasov-Poisson to Schrödinger-Poisson: dark matter simulation with a quantum variational time evolution algorithm. Phys. Rev. Res. 6, 013282. https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.6.013282Google Scholar
Chan, G.K.-L. & Head-Gordon, M. 2002 Highly correlated calculations with polynomial cost algorithm: a study of the density matrix renormalization group. J. Chem. Phys. 116, 4462.Google Scholar
Coughlin, J., Hu, J. & Shumlak, U. 2023 Robust and conservative dynamical low-rank methods for the Vlasov equation via a novel macro-micro decomposition. arXiv:2311.09425.Google Scholar
Courant, R., Friedrichs, K. & Lewy, H. 1967 On the partial difference equations of mathematical physics. IBM J. Res. Develop. 11 (2), 215–234.Google Scholar
Dolgov, S. 2014 Tensor product methods in numerical simulation of high-dimensional dynamical problems. PhD thesis, Leipzig University.Google Scholar
Dolgov, S. & Khoromskij, B. 2013 Two-level Tucker-TT-QTT format for optimized tensor calculus. SIAM J. Matrix Anal. Applics. 34, 593–623.Google Scholar
Dolgov, S.V., Khoromskij, B.N. & Oseledets, I.V. 2012 Fast solution of parabolic problems in the tensor train/quantized tensor train format with initial application to the Fokker–Planck equation. SIAM J. Sci. Comput. 34 (6), A3016–A3038.Google Scholar
Dolgov, S.V. & Savostyanov, D.V. 2014 Alternating minimal energy method for linear systems in higher dimensions. SIAM J. Sci. Comput. 36 (5), A2248–A2271.Google Scholar
Durran, D.R. 2010 Numerical Methods for Fluid Dynamics: With Applications to Geophysics. Springer.Google Scholar
Einkemmer, L. 2023 Accelerating the simulation of kinetic shear Alfvén waves with a dynamical low-rank approximation. arXiv:2306.17526.Google Scholar
Einkemmer, L. & Jospeh, I. 2021 A mass, momentum, and energy conservation dynamical low-rank scheme for the Vlasov equation. J. Comput. Phys. 443, 110495.Google Scholar
Einkemmer, L. & Lubich, C. 2018 A low-rank projector-splitting integrator for the Vlasov–Poisson equation. SIAM J. Sci. Comput. 40 (5), B1330–B1360.Google Scholar
Einkemmer, L. & Lubich, C. 2019 A quasi-conservative dynamical low-rank algorithm for the Vlasov equation. SIAM J. Sci. Comput. 41 (5), B1061–B1081.Google Scholar
Einkemmer, L., Ostermann, A. & Piazzola, C. 2020 A low-rank projector-splitting integrator for the Vlasov–Maxwell equations with divergence correction. J. Comput. Phys. 403, 109063.Google Scholar
Frenkel, J. 1934 Wave Mechanics: Advanced General Theory. Clarendon Press.Google Scholar
Garcia-Ripoll, J.J. 2021 Quantum-inspired algorithms for multivariate analysis: from interpolation to partial differential equation. Quantum 5, 431.Google Scholar
Gourianov, N. 2022 Exploiting the structure of turbulence with tensor networks. PhD thesis, University of Oxford.Google Scholar
Gourianov, N., Lubasch, M., Dolgov, S., van den Berg, Q.Y., Babaee, H., Givi, P., Kiffner, M. & Jaksch, D. 2022 A quantum inspired approach to exploit turbulence structures. Nature Comput. Sci. 2, 30–37.Google Scholar
Gray, J. 2018 quimb: a python library for quantum information and many-body calculations. J. Open Sour. Softw. 3 (29), 819.Google Scholar
Haegeman, J., Lubich, C., Oseledets, I., Vandereycken, B. & Verstraete, F. 2016 Unifying time evolution and optimization with matrix product states. Phys. Rev. B 94, 165116.Google Scholar
Hakim, A., Francisquez, M., Juno, J. & Hammett, G.W. 2020 Conservative discontinuous galerkin schemes for nonlinear Dougherty–Fokker–Planck collision operators. J. Plasma Phys. 86 (4), 905860403.Google Scholar
Hakim, A. & Juno, J. 2020 Alias-free, matrix-free, and quadrature-free discontinuous Galerkin algorithms for (plasma) kinetic equations. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis. IEEE Press.Google Scholar
Harris, E.G. 1962 On a plasma sheath separating regions of oppositely directed magnetic field. Il Nuovo Cimento (1955–1965) 23, 115–121.Google Scholar
Jaksch, D., Givi, P., Daley, A.J. & Rung, T. 2023 Variational quantum algorithms for computational fluid dynamics. AIAA J. 61 (5), 1885–1894.Google Scholar
Juno, J., Hakim, A., TenBarge, J., Shi, E. & Dorland, W. 2018 Discontinuous Galerkin algorithms for fully kinetic plasmas. J. Comput. Phys. 353, 110–147.Google Scholar
Kazeev, V.A. & Khoromskij, B.N. 2012 Low-rank explicit QTT representation of the Laplace operator and its inverse. SIAM J. Matrix Anal. Applics. 33 (3), 742–758.Google Scholar
Kazeev, V.A., Khoromskij, B.N. & Tyrtyshnikov, E.E. 2013 a Multilevel Toeplitz matrices generated by tensor-structured vectors and convolution with logarithmic complexity. SIAM J. Sci. Comput. 35 (3), A1511–A1536.Google Scholar
Kazeev, V., Oseledets, I., Rakhuba, M. & Schwab, C. 2017 QTT-finite-element approximation for multiscale problems I: model problems in one dimension. Adv. Comput. Math. 43, 411–442.Google Scholar
Kazeev, V., Oseledets, I., Rakhuba, M. & Schwab, C. 2022 Quantized tensor FEM for multiscale problems: diffusion problems in two and three dimensions. Multiscale Model. Simul. 20 (3), 893–935.Google Scholar
Kazeev, V., Reichmann, O. & Schwab, C. 2013 b Low-rank tensor structure of linear diffusion operators in the TT and QTT formats. Linear Algebr. Applics. 438 (11), 4024–4221.Google Scholar
Kazeev, V. & Schwab, C. 2018 Quantized tensor-structured finite elements for second-order elliptic PDEs in two dimensions. Numer. Math. 138, 133–190.Google Scholar
Khoromskij, B.N. 2011 $O(d\log {N})$-quantics approximation of $N$-$d$ tensors in high-dimensional numerical modeling. Constr. Approx. 34, 257–280.Google Scholar
Khoromskij, B.N., Oseledets, I.V. & Schneider, R. 2012 Efficient time-stepping scheme for dynamics on TT-manifolds. arXiv:24/2012.Google Scholar
Kiffner, M. & Jaksch, D. 2023 Tensor network reduced order models for wall-bounded flows. Phys. Rev. Fluids. 8, 124101. https://journals.aps.org/prfluids/abstract/10.1103/PhysRevFluids.8.124101Google Scholar
Kormann, K. 2015 A semi-Lagrangian Vlasov solver in tensor train format. SIAM J. Sci. Comput. 37 (4), B613–B632.Google Scholar
Kornev, E., Dolgov, S., Pinto, K., Pflitsch, M., Perelshtein, M. & Melnikov, A. 2023 Numerical solution of the incompressible Navier–Stokes equations for chemical mixers via quantum-inspired tensor train finite element method. arXiv:2305.10784.Google Scholar
Lasser, C. & Su, C. 2022 Various variational approximations of quantum dynamics. J. Math. Phys. 63, 072107.Google Scholar
Lindsey, M. 2023 Multiscale interpolative construction of quantized tensor trains. arXiv:2311.12554.Google Scholar
Lubasch, M., Joo, J., Moinier, P., Kiffner, M. & Jaksch, D. 2020 Variational quantum algorithms for nonlinear problems. Phys. Rev. A 101 (1), 010301(R).Google Scholar
Lubasch, M., Moinier, P. & Jaksch, D. 2018 Multigrid renormalization. J. Comput. Phys. 372, 587–602.Google Scholar
McCulloch, I.P. 2007 From density-matrix renormalization group to matrix product states. J. Stat. Mech. 2007, P10014.Google Scholar
Orszag, S.A. & Tang, C.-M. 1979 Small-scale structure of two-dimensional magnetohydrodynamic turbulence. J. Fluid Mech. 90 (1), 129–143.Google Scholar
Oseledets, I.V. 2009 Approximation of matrices with logarthmic number of parameters. Dokl. Math. 80, 653–654.Google Scholar
Oseledets, I.V. 2010 Approximation of $2^d \times 2^d$ matrices using tensor decomposition. SIAM J. Sci. Comput. 31 (4), 2130–2145.Google Scholar
Oseledets, I.V. & Dolgov, S.V. 2012 Solution of linear systems and matrix inversion in the TT-format. SIAM J. Sci. Comput. 34 (5), A2718–A2739.Google Scholar
Oseledets, I.V. & Tyrtyshnikov, E. 2010 TT-cross approximation for multidimensional arrays. Linear Algebra Appl. 432, 70–88.Google Scholar
Oseledets, I.V. & Tyrtyshnikov, E. 2011 Algebraic wavelet transform via quantics tensor train decomposition. SIAM J. Sci. Comput. 33 (3), 1315–1328.Google Scholar
Paeckel, S., Köhler, T., Swoboda, A., Manmana, S.R., Schöllwöck, U. & Hubig, C. 2019 Time-evolution methods for matrix-product states. Ann. Phys. 411, 167998.Google Scholar
Peddinti, R.D., Pisoni, S., Marini, A., Lott, P., Argentieri, H., Tiunov, E. & Aolita, L. 2023 Complete quantum-inspired framework for computational fluid dynamics. arXiv:2308.12972.Google Scholar
Schmitz, H. & Grauer, R. 2006 Kinetic Vlasov simulations of collisionless magnetic reconnection. Phys. Plasmas 13 (9), 092309.Google Scholar
Schollwöck, U. 2011 The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 326, 96–192.Google Scholar
Secular, P., Gourianov, N., Lubasch, M., Dolgov, S., Clark, S.R. & Jaksch, D. 2020 Parallel time-dependent variational principle algorithm for matrix product states. Phys. Rev. B 101, 235123.Google Scholar
Sonneveld, P. 1989 CGS, a fast Lanczos-type solver for nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 10, 36–52.Google Scholar
Vidal, G. 2003 Efficient classical simulation of slightly entangled quantum computations. Phys. Rev. Lett. 91, 147902.Google Scholar
White, S.R. 1993 Density matrix algorithms for quantum renormalization groups. Phys. Rev. B 48, 10345.Google Scholar
White, S.R. 2005 Density matrix renormalization group algorithms with a single center site. Phys. Rev. B 72, 180403(R).Google Scholar
Yang, M. & White, S.R. 2020 Time-dependent variational principle with ancillary Krylov subspace. Phys. Rev. B 102 (9), 094315.Google Scholar
Ye, E. & Loureiro, N.F.G. 2022 Quantum-inspired method for solving the Vlasov–Poisson equations. Phys. Rev. E 106, 035208.Google Scholar
Supplementary material: File

Ye and Loureiro supplementary material

Ye and Loureiro supplementary material
Download Ye and Loureiro supplementary material(File)
File 3.6 MB