Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-04-26T00:24:49.893Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear electron scattering by electrostatic waves in collisionless shocks

Published online by Cambridge University Press:  07 March 2024

Sergei R. Kamaletdinov Open the ORCID record for Sergei R. Kamaletdinov [Opens in a new window] ,
Ivan Y. Vasko  and
Anton V. Artemyev Open the ORCID record for Anton V. Artemyev [Opens in a new window]
Sergei R. Kamaletdinov*
Affiliation:
Space Research Institute of the Russian Academy of Sciences (IKI), 84/32 Profsoyuznaya Str., Moscow 117997, Russia Faculty of Physics, National Research University Higher School of Economics, 21/4 Staraya Basmannaya Ulitsa, Moscow 105066, Russia Department of Earth, Planetary, and Space Sciences, University of California, 595 Charles E Young Dr E, Los Angeles, CA 90095, USA
Ivan Y. Vasko
Affiliation:
Space Research Institute of the Russian Academy of Sciences (IKI), 84/32 Profsoyuznaya Str., Moscow 117997, Russia William B. Hanson Center for Space Sciences, University of Texas at Dallas, 800 W Campbell Rd., Richardson, TX 75080, USA
Anton V. Artemyev
Affiliation:
Space Research Institute of the Russian Academy of Sciences (IKI), 84/32 Profsoyuznaya Str., Moscow 117997, Russia Department of Earth, Planetary, and Space Sciences, University of California, 595 Charles E Young Dr E, Los Angeles, CA 90095, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a theoretical analysis of electron pitch-angle scattering by ion-acoustic electrostatic fluctuations present in the Earth's bow shock and, presumably, collisionless shocks in general. We numerically simulate electron interaction with a single wave packet to demonstrate the scattering through phase bunching and phase trapping and quantify electron pitch-angle scattering in dependence on the wave amplitude and wave normal angle to the local magnetic field. The iterative mapping technique is used to model pitch-angle scattering of electrons by a large number of wave packets, which have been reported in the Earth's bow shock. Assuming that successive electron scatterings are not correlated, we revealed that the long-term dynamics of electrons is diffusive. The diffusion coefficient depends on the ratio $\varPhi _0/W$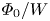 between the wave packet amplitude and electron energy, $D\propto (\varPhi _0/W)^{\nu }$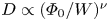. A quasi-linear scaling ($\nu \approx 2$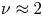) is observed for sufficiently small wave amplitudes, $\varPhi _0\lesssim 10^{-3}W$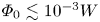, while the diffusion is nonlinear ($1<\nu <2$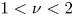) above this threshold. We show that pitch-angle diffusion of ${\lesssim }1$ 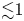keV electrons in the Earth's bow shock can be nonlinear. The corresponding diffusion coefficient scales with the intensity $E_{w}^{2}$ 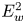of the electrostatic fluctuations in a nonlinear fashion, $D\propto E_{w}^{\nu }$ 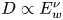with $\nu <2$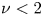, while its expected values in the Earth's bow shock are $D\sim 0.1\unicode{x2013}100$ 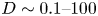$(T_{e}/W)^{\nu -1/2}\,{\rm rad}^{2}\,{\rm s}^{-1}$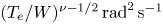. We speculate that in the Earth's quasi-perpendicular bow shock the stochastic shock drift acceleration mechanism with pitch-angle scattering provided by the electrostatic fluctuations can contribute to the acceleration of thermal electrons up to approximately 1 keV. The potential effects of a finite perpendicular coherence scale of the wave packets on the efficiency of electron scattering are discussed.

Keywords

plasma nonlinear phenomenaplasma wavesplasma simulation
Type
Research Article
Information
Journal of Plasma Physics , Volume 90 , Issue 2 , April 2024 , 905900201
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Albert, J.M., Meredith, N.P. & Horne, R.B. 2009 Three-dimensional diffusion simulation of outer radiation belt electrons during the 9 October 1990 magnetic storm. J. Geophys. Res. 114, 9214.Google Scholar
Amano, T. & Hoshino, M. 2009 Nonlinear evolution of Buneman instability and its implication for electron acceleration in high Mach number collisionless perpendicular shocks. Phys. Plasmas 16 (10), 102901.CrossRefGoogle Scholar
Amano, T., Katou, T., Kitamura, N., Oka, M., Matsumoto, Y., Hoshino, M., Saito, Y., Yokota, S., Giles, B.L., Paterson, W.R., et al. 2020 Observational evidence for stochastic shock drift acceleration of electrons at the Earth's bow shock. Phys. Rev. Lett. 124 (6), 065101.CrossRefGoogle ScholarPubMed
Amano, T., Matsumoto, Y., Bohdan, A., Kobzar, O., Matsukiyo, S., Oka, M., Niemiec, J., Pohl, M. & Hoshino, M. 2022 Nonthermal electron acceleration at collisionless quasi-perpendicular shocks. Rev. Mod. Plasma Phys. 6 (1), 29.CrossRefGoogle Scholar
Artemyev, A.V., Neishtadt, A.I., Vasiliev, A.A. & Mourenas, D. 2016 Kinetic equation for nonlinear resonant wave-particle interaction. Phys. Plasmas 23 (9), 090701.CrossRefGoogle Scholar
Artemyev, A.V., Neishtadt, A.I., Vasiliev, A.A. & Mourenas, D. 2021 Transitional regime of electron resonant interaction with whistler-mode waves in inhomogeneous space plasma. Phys. Rev. E 104 (5), 055203.CrossRefGoogle ScholarPubMed
Artemyev, A.V., Shi, X., Liu, T.Z., Zhang, X.J., Vasko, I. & Angelopoulos, V. 2022 Electron resonant interaction with whistler waves around foreshock transients and the bow shock behind the terminator. J. Geophys. Res. 127 (2), e29820.CrossRefGoogle Scholar
Balikhin, M., Walker, S., Treumann, R., Alleyne, H., Krasnoselskikh, V., Gedalin, M., Andre, M., Dunlop, M. & Fazakerley, A. 2005 Ion sound wave packets at the quasiperpendicular shock front. Geophys. Res. Lett. 32 (24), L24106.CrossRefGoogle Scholar
Breneman, A.W., Cattell, C.A., Kersten, K., Paradise, A., Schreiner, S., Kellogg, P.J., Goetz, K. & Wilson, L.B. 2013 STEREO and Wind observations of intense cyclotron harmonic waves at the Earth's bow shock and inside the magnetosheath. J. Geophys. Res. 118 (12), 7654–7664.CrossRefGoogle Scholar
Burch, J.L., Moore, T.E., Torbert, R.B. & Giles, B.L. 2016 Magnetospheric multiscale overview and science objectives. Space Sci. Rev. 199, 5–21.CrossRefGoogle Scholar
Cargill, P.J. & Papadopoulos, K. 1988 A mechanism for strong shock electron heating in supernova remnants. Astrophys. J. Lett. 329, L29.CrossRefGoogle Scholar
Ergun, R.E., Tucker, S., Westfall, J., Goodrich, K.A., Malaspina, D.M., Summers, D., Wallace, J., Karlsson, M., Mack, J., Brennan, N., et al. 2016 The axial double probe and fields signal processing for the MMS mission. Space Sci. Rev. 199, 167–188.CrossRefGoogle Scholar
Fuselier, S.A. & Gurnett, D.A. 1984 Short wavelength ion waves upstream of the Earth's bow shock. J. Geophys. Res. 89 (A1), 91–104.CrossRefGoogle Scholar
Gedalin, M. 2020 Large-scale versus small-scale fields in the shock front: effect on the particle motion. Astrophys. J. 895 (1), 59.CrossRefGoogle Scholar
Gedalin, M., Golan, M., Vink, J., Ganushkina, N. & Balikhin, M. 2023 Electron heating in shocks: statistics and comparison. J. Geophys. Res. 128 (9), e2023JA031627.CrossRefGoogle Scholar
Ghavamian, P., Schwartz, S.J., Mitchell, J., Masters, A. & Laming, J.M. 2013 Electron-ion temperature equilibration in collisionless shocks: the supernova remnant-solar wind connection. Space Sci. Rev. 178 (2–4), 633–663.CrossRefGoogle Scholar
Gosling, J.T., Thomsen, M.F., Bame, S.J. & Russell, C.T. 1989 Suprathermal electrons at Earth's bow shock. J. Geophys. Res. 94 (A8), 10011–10025.CrossRefGoogle Scholar
Graham, D.B., Khotyaintsev, Y.V., Vaivads, A. & André, M. 2016 Electrostatic solitary waves and electrostatic waves at the magnetopause. J. Geophys. Res. 121 (4), 3069–3092.CrossRefGoogle Scholar
Gurnett, D.A. 1985 Plasma Waves and Instabilities. Geophysical Monograph Series, vol. 35, pp. 207–224. American Geophysical Union.Google Scholar
Gurnett, D.A. & Frank, L.A. 1978 Ion acoustic waves in the solar wind. J. Geophys. Res. 83 (A1), 58–74.CrossRefGoogle Scholar
Hull, A.J., Larson, D.E., Wilber, M., Scudder, J.D., Mozer, F.S., Russell, C.T. & Bale, S.D. 2006 Large-amplitude electrostatic waves associated with magnetic ramp substructure at Earth's bow shock. Geophys. Res. Lett. 33 (15), L15104.CrossRefGoogle Scholar
Johlander, A., Khotyaintsev, Y.V., Dimmock, A.P., Graham, D.B. & Lalti, A. 2023 Electron heating scales in collisionless shocks measured by MMS. Geophys. Res. Lett. 50 (5), e2022GL100400.CrossRefGoogle Scholar
Kamaletdinov, S., Vasko, I., Artemyev, A., Wang, R. & Mozer, F. 2022 Quantifying electron scattering by electrostatic solitary waves in the Earth's bow shock. Phys. Plasmas 29 (8), 082301.CrossRefGoogle Scholar
Kamaletdinov, S.R., Vasko, I.Y., Wang, R., Artemyev, A.V., Yushkov, E.V. & Mozer, F.S. 2022 Slow electron holes in the Earth's bow shock. Phys. Plasmas 29 (9), 092303.CrossRefGoogle Scholar
Kennel, C.F. & Engelmann, F. 1966 Velocity space diffusion from weak plasma turbulence in a magnetic field. Phys. Fluids 9, 2377–2388.CrossRefGoogle Scholar
Krasnoselskikh, V., Balikhin, M., Walker, S.N., Schwartz, S., Sundkvist, D., Lobzin, V., Gedalin, M., Bale, S.D., Mozer, F., Soucek, J., et al. 2013 The dynamic quasiperpendicular shock: cluster discoveries. Space Sci. Rev. 178, 535–598.CrossRefGoogle Scholar
Lalti, A., Khotyaintsev, Y.V., Graham, D.B., Vaivads, A., Steinvall, K. & Russell, C.T. 2022 Whistler waves in the foot of quasi-perpendicular supercritical shocks. J. Geophys. Res. 127 (5), e2021JA029969.CrossRefGoogle Scholar
Lindqvist, P.-A., Olsson, G., Torbert, R.B., King, B., Granoff, M., Rau, D., Needell, G., Turco, S., Dors, I., Beckman, P., et al. 2016 The spin-plane double probe electric field instrument for MMS. Space Sci. Rev. 199, 137–165.CrossRefGoogle Scholar
Liu, C.M., Vaivads, A., Graham, D.B., Khotyaintsev, Y.V., Fu, H.S., Johlander, A., André, M. & Giles, B.L. 2019 Ion-beam-driven intense electrostatic solitary waves in reconnection jet. Geophys. Res. Lett. 46 (22), 12702–12710.CrossRefGoogle Scholar
Lukin, A.S., Artemyev, A.V. & Petrukovich, A.A. 2021 On application of stochastic differential equations for simulation of nonlinear wave-particle resonant interactions. Phys. Plasmas 28 (9), 092904.CrossRefGoogle Scholar
Lyons, L.R. 1974 Pitch angle and energy diffusion coefficients from resonant interactions with ion-cyclotron and whistler waves. J. Plasma Phys. 12, 417–432.CrossRefGoogle Scholar
Mangeney, A., Lacombe, C., Maksimovic, M., Samsonov, A.A., Cornilleau-Wehrlin, N., Harvey, C.C., Bosqued, J.M. & Trávníček, P. 2006 Cluster observations in the magnetosheath. Part 1. Anisotropies of the wave vector distribution of the turbulence at electron scales. Ann. Geophys. 24 (12), 3507–3521.CrossRefGoogle Scholar
Markevitch, M. & Vikhlinin, A. 2007 Shocks and cold fronts in galaxy clusters. Phys. Rep. 443 (1), 1–53.CrossRefGoogle Scholar
Mozer, F.S., Agapitov, O., Artemyev, A., Drake, J.F., Krasnoselskikh, V., Lejosne, S. & Vasko, I. 2015 Time domain structures: what and where they are, what they do, and how they are made. Geophys. Res. Lett. 42, 3627–3638.CrossRefGoogle Scholar
Mozer, F.S., Bonnell, J.W., Bowen, T.A., Schumm, G. & Vasko, I.Y. 2020 Large-amplitude, wideband, Doppler-shifted, ion acoustic waves observed on the parker solar probe. Astrophys. J. 901 (2), 107.CrossRefGoogle Scholar
Mozer, F.S., Cattell, C.A., Temerin, M., Torbert, R.B., von Glinski, S., Woldorff, M. & Wygant, J. 1979 The DC and AC electric field, plasma density, plasma temperature, and field-aligned current experiments on the S3-3 satellite. J. Geophys. Res. 84, 5875–5884.CrossRefGoogle Scholar
Muschietti, L. & Lembège, B. 2017 Two-stream instabilities from the lower-hybrid frequency to the electron cyclotron frequency: application to the front of quasi-perpendicular shocks. Ann. Geophys. 35 (5), 1093–1112.CrossRefGoogle Scholar
Neishtadt, A.I., Chaikovskii, D.K. & Chernikov, A.A. 1991 Adiabatic chaos and diffusion of particles. Zh. Eksp. Teor. Fiz. 99, 763–776.Google Scholar
Nunn, D. 1971 Wave-particle interactions in electrostatic waves in an inhomogeneous medium. J. Plasma Phys. 6, 291.CrossRefGoogle Scholar
Oka, M., Otsuka, F., Matsukiyo, S., Wilson, L.B. III, Argall, M.R., Amano, T., Phan, T.D., Hoshino, M., Le Contel, O., Gershman, D.J., et al. 2019 Electron scattering by low-frequency whistler waves at Earth's bow shock. Astrophys. J. 886 (1), 53.CrossRefGoogle Scholar
Oka, M., Terasawa, T., Seki, Y., Fujimoto, M., Kasaba, Y., Kojima, H., Shinohara, I., Matsui, H., Matsumoto, H., Saito, Y., et al. 2006 Whistler critical Mach number and electron acceleration at the bow shock: geotail observation. Geophys. Res. Lett. 33 (24), L24104.CrossRefGoogle Scholar
Oka, M., Wilson, L.B. III, Phan, T.D., Hull, A.J., Amano, T., Hoshino, M., Argall, M.R., Le Contel, O., Agapitov, O., Gershman, D.J., et al. 2017 Electron scattering by high-frequency whistler waves at Earth's bow shock. Astrophys. J. Lett. 842, L11.CrossRefGoogle Scholar
Omura, Y., Matsumoto, H., Nunn, D. & Rycroft, M.J. 1991 A review of observational, theoretical and numerical studies of VLF triggered emissions. J. Atmos. Terr. Physi. 53, 351–368.CrossRefGoogle Scholar
Omura, Y., Miyashita, Y., Yoshikawa, M., Summers, D., Hikishima, M., Ebihara, Y. & Kubota, Y. 2015 Formation process of relativistic electron flux through interaction with chorus emissions in the Earth's inner magnetosphere. J. Geophys. Res. 120, 9545–9562.CrossRefGoogle Scholar
Page, B., Vasko, I.Y., Artemyev, A.V. & Bale, S.D. 2021 Generation of high-frequency whistler waves in the Earth's quasi-perpendicular bow shock. Astrophys. J. Lett. 919 (2), L17.CrossRefGoogle Scholar
Pollock, C., Moore, T., Jacques, A., Burch, J., Gliese, U., Saito, Y., Omoto, T., Avanov, L., Barrie, A., Coffey, V., et al. 2016 Fast plasma investigation for magnetospheric multiscale. Space Sci. Rev. 199, 331–406.CrossRefGoogle Scholar
Raymond, J.C., Ghavamian, P., Bohdan, A., Ryu, D., Niemiec, J., Sironi, L., Tran, A., Amato, E., Hoshino, M., Pohl, M., et al. 2023 Electron-ion temperature ratio in astrophysical shocks. Astrophys. J. 949 (2), 50.CrossRefGoogle Scholar
Rodriguez, P. 1979 Magnetosheath electrostatic turbulence. J. Geophys. Res. 84 (A3), 917–930.CrossRefGoogle Scholar
Russell, C.T., Anderson, B.J., Baumjohann, W., Bromund, K.R., Dearborn, D., Fischer, D., Le, G., Leinweber, H.K., Leneman, D., Magnes, W., et al. 2016 The magnetospheric multiscale magnetometers. Space Sci. Rev. 199, 189–256.CrossRefGoogle Scholar
Scudder, J.D. 1995 A review of the physics of electron heating at collisionless shocks. Adv. Space Res. 15, 181–223.CrossRefGoogle Scholar
Shen, Y., Vasko, I.Y., Artemyev, A., Malaspina, D.M., Chu, X., Angelopoulos, V. & Zhang, X.-J. 2021 Realistic electron diffusion rates and lifetimes due to scattering by electron holes. J. Geophys. Res. 126 (9), e29380.CrossRefGoogle Scholar
Shklyar, D.R. & Matsumoto, H. 2009 Oblique whistler-mode waves in the inhomogeneous magnetospheric plasma: resonant interactions with energetic charged particles. Surv. Geophys. 30, 55–104.CrossRefGoogle Scholar
Temerin, M., Cattell, C., Lysak, R., Hudson, M., Torbert, R.B., Mozer, F.S., Sharp, R.D. & Kintner, P.M. 1981 The small-scale structure of electrostatic shocks. J. Geophys. Res. 86 (A13), 11278–11298.CrossRefGoogle Scholar
Vasko, I.Y., Agapitov, O.V., Mozer, F.S., Artemyev, A.V., Krasnoselskikh, V.V. & Bonnell, J.W. 2017 Diffusive scattering of electrons by electron holes around injection fronts. J. Geophys. Res. 122, 3163–3182.CrossRefGoogle Scholar
Vasko, I.Y., Krasnoselskikh, V.V., Mozer, F.S. & Artemyev, A.V. 2018 a Scattering by the broadband electrostatic turbulence in the space plasma. Phys. Plasmas 25 (7), 072903.CrossRefGoogle Scholar
Vasko, I.Y., Mozer, F.S., Bale, S.D. & Artemyev, A.V. 2022 Ion-acoustic waves in a quasi-perpendicular Earth's bow shock. Geophys. Res. Lett. 49 (11), e98640.CrossRefGoogle Scholar
Vasko, I.Y., Mozer, F.S., Krasnoselskikh, V.V., Artemyev, A.V., Agapitov, O.V., Bale, S.D., Avanov, L., Ergun, R., Giles, B., Lindqvist, P.-A., et al. 2018 b Solitary waves across supercritical quasi-perpendicular shocks. Geophys. Res. Lett. 45, 5809–5817.CrossRefGoogle Scholar
Vasko, I.Y., Wang, R., Mozer, F.S., Bale, S.D. & Artemyev, A.V. 2020 On the nature and origin of bipolar electrostatic structures in the Earth's bow shock. Front. Phys. 8, 156.CrossRefGoogle Scholar
Vedenov, A.A., Velikhov, E. & Sagdeev, R. 1962 Quasilinear theory of plasma oscillations. Nucl. Fusion Suppl. 2, 465–475.Google Scholar
Walt, M. 1994 Introduction to geomagnetically trapped radiation. Camb. Atmos. Space Sci. Ser. Cambridge University Press.CrossRefGoogle Scholar
Wang, R., Vasko, I.Y., Artemyev, A.V., Holley, L.C., Kamaletdinov, S.R., Lotekar, A. & Mozer, F.S. 2022 Multisatellite observations of ion holes in the Earth's plasma sheet. Geophys. Res. Lett. 49 (8), e97919.Google Scholar
Wang, R., Vasko, I.Y., Mozer, F.S., Bale, S.D., Artemyev, A.V., Bonnell, J.W., Ergun, R., Giles, B., Lindqvist, P.A., Russell, C.T., et al. 2020 Electrostatic turbulence and Debye-scale structures in collisionless shocks. Astrophys. J. Lett. 889 (1), L9.CrossRefGoogle Scholar
Wang, R., Vasko, I.Y., Mozer, F.S., Bale, S.D., Kuzichev, I.V., Artemyev, A.V., Steinvall, K., Ergun, R., Giles, B., Khotyaintsev, Y., et al. 2021 Electrostatic solitary waves in the Earth's bow shock: nature, properties, lifetimes, and origin. J. Geophys. Res. 126 (7), e29357.Google Scholar
Wilson, L.B., Sibeck, D.G., Breneman, A.W., Contel, O.L., Cully, C., Turner, D.L., Angelopoulos, V. & Malaspina, D.M. 2014 Quantified energy dissipation rates in the terrestrial bow shock: 2. Waves and dissipation. J. Geophys. Res. 119, 6475–6495.CrossRefGoogle Scholar
Zhang, X.-J., Artemyev, A., Angelopoulos, V., Tsai, E., Wilkins, C., Kasahara, S., Mourenas, D., Yokota, S., Keika, K., Hori, T., et al. 2022 Superfast precipitation of energetic electrons in the radiation belts of the Earth. Nat. Commun. 13, 1611.CrossRefGoogle ScholarPubMed