No CrossRef data available.
Published online by Cambridge University Press: 22 October 2024
We have derived a necessary condition for the achievement of breakeven in axisymmetric plasmas with zero toroidal field and confined by a dipole magnetic field (B. Lehnert, Nature, vol. 181, 1958, p. 4605; A. Hasegawa, Comments Plasma Phys. Control. Fusion, vol. 11, no. 3, 1987). Excellent MHD stability, high values of $\beta$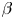 (up to $26$
(up to $26$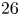 %) and good confinement properties awaken the interest of private investors after years of neglect due to lack of public funding and competing alternative lines of research like the tokamak. Starting from a requirement of self-consistency between the balances of momentum and energy in a dipole-confined, two-species plasma and assuming a Maxwellian distribution function for ions and electrons, we derive a necessary condition for breakeven. This condition is more stringent than the Lawson criterion because of the lack of a stabilizing toroidal field. For a given current flowing across the toroidal coil internal to the plasma, the crucial factor at stake is the ratio between the radius of the main toroidal coil and the radius of the vacuum chamber.
%) and good confinement properties awaken the interest of private investors after years of neglect due to lack of public funding and competing alternative lines of research like the tokamak. Starting from a requirement of self-consistency between the balances of momentum and energy in a dipole-confined, two-species plasma and assuming a Maxwellian distribution function for ions and electrons, we derive a necessary condition for breakeven. This condition is more stringent than the Lawson criterion because of the lack of a stabilizing toroidal field. For a given current flowing across the toroidal coil internal to the plasma, the crucial factor at stake is the ratio between the radius of the main toroidal coil and the radius of the vacuum chamber.