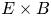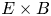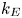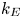1. Introduction
Turbulent transport processes have been established to largely determine the outward power and particle fluxes in the plasma edge of tokamaks (Scott Reference Scott2003; Wesson Reference Wesson2004; Fundamenski Reference Fundamenski2010). Thus, properly modelling these processes is crucial to correctly predicting the load on the divertor. However, doing so using acceptable computational resources remains challenging. The aim of this paper is to provide a generally valid mean-field equation set to serve as a theoretical basis in the development of self-consistent, physics-based mean-field turbulent transport models for plasma edge transport codes.
The turbulent fluctuations driving the transport perpendicular to the magnetic field lines occur at very small time and length scales, typically of the order of $(\rho \varOmega /L_\perp )^{-1}$![]() and $\rho$
and $\rho$![]() , respectively, with $\varOmega$
, respectively, with $\varOmega$![]() and $\rho$
and $\rho$![]() the ion gyro-frequency and radius and $L_\perp$
the ion gyro-frequency and radius and $L_\perp$![]() a typical length scale of the average perpendicular gradients of the profiles (Scott Reference Scott2003, Reference Scott2007; Fundamenski Reference Fundamenski2010). At first order, the details of this very fine scale dynamics are not of interest to the design of future fusion reactors. Moreover, they are very expensive to resolve computationally since very fine meshes and time steps are required. It is rather the average behaviour of the turbulence and the resulting average profiles of density and pressure that are of interest. These averaged or so-called mean-field quantities of the turbulent flow are calculated in mean-field transport codes such as SOLPS-ITER (Wiesen et al. Reference Wiesen, Reiter, Kotov, Baelmans, Dekeyser, Kukushkin, Lisgo, Pitts, Rozhansky and Saibene2015; Bonnin et al. Reference Bonnin, Dekeyser, Pitts, Coster, Voskoboynikov and Wiesen2016), SOLEDGE2D (Bufferand et al. Reference Bufferand, Ciraolo, Marandet, Bucalossi, Ghendrih, Gunn, Mellet, Tamain, Leybros and Fedorczak2015), UEDGE (Rognlien et al. Reference Rognlien, Ryutov, Mattor and Porter1999), EDGE2D-EIRENE (Reiter Reference Reiter1992; Wiesen Reference Wiesen2006; Simonini et al. Reference Simonini, Corrigan, Radford, Spence and Taroni2018) and DivOpt (Dekeyser Reference Dekeyser2014; Dekeyser, Reiter & Baelmans Reference Dekeyser, Reiter and Baelmans2014), which are computationally less demanding.
a typical length scale of the average perpendicular gradients of the profiles (Scott Reference Scott2003, Reference Scott2007; Fundamenski Reference Fundamenski2010). At first order, the details of this very fine scale dynamics are not of interest to the design of future fusion reactors. Moreover, they are very expensive to resolve computationally since very fine meshes and time steps are required. It is rather the average behaviour of the turbulence and the resulting average profiles of density and pressure that are of interest. These averaged or so-called mean-field quantities of the turbulent flow are calculated in mean-field transport codes such as SOLPS-ITER (Wiesen et al. Reference Wiesen, Reiter, Kotov, Baelmans, Dekeyser, Kukushkin, Lisgo, Pitts, Rozhansky and Saibene2015; Bonnin et al. Reference Bonnin, Dekeyser, Pitts, Coster, Voskoboynikov and Wiesen2016), SOLEDGE2D (Bufferand et al. Reference Bufferand, Ciraolo, Marandet, Bucalossi, Ghendrih, Gunn, Mellet, Tamain, Leybros and Fedorczak2015), UEDGE (Rognlien et al. Reference Rognlien, Ryutov, Mattor and Porter1999), EDGE2D-EIRENE (Reiter Reference Reiter1992; Wiesen Reference Wiesen2006; Simonini et al. Reference Simonini, Corrigan, Radford, Spence and Taroni2018) and DivOpt (Dekeyser Reference Dekeyser2014; Dekeyser, Reiter & Baelmans Reference Dekeyser, Reiter and Baelmans2014), which are computationally less demanding.
However, the current approach in mean-field modelling is, basically, to take the full (fluid) turbulence equations and to evaluate them with mean-field quantities. In addition to this, ad hoc diffusion or advection terms are added to model the radial turbulent transport. Due to turbulent fluctuations, these equations are not equivalent to the turbulent equations and forego the actual dynamics of the turbulence. This paper, on the other hand, derives mean-field equations that do correspond to the underlying turbulence equations analytically through a rigorous averaging methodology. This averaging operation introduces terms which depend on the correlation between turbulent fluctuations in the mean-field equations. These ‘closure terms’ require modelling.
Rather recently, a number of models have been proposed that relate the mean-field turbulent transport coefficients to the characteristics of the underlying turbulence (Miki et al. Reference Miki, Diamond, Gürcan, Tynan, Estrada, Schmitz and Xu2012; Bufferand et al. Reference Bufferand, Ciraolo, Ghendrih, Marandet, Bucalossi, Colin, Fedorczak, Galassi, Gunn and Leybros2016; Baschetti et al. Reference Baschetti, Bufferand, Ciraolo, Fedorczak, Ghendrih, Serre and Tamain2018a,Reference Baschetti, Bufferand, Ciraolo and Ghendrihb, Reference Baschetti, Bufferand, Ciraolo, Fedorczak, Ghendrih, Tamain and Serre2019, Reference Baschetti, Bufferand, Ciraolo, Ghendrih, Serre and Tamain2021; Carli et al. Reference Carli, Dekeyser, Coosemans, Dejarnac, Komm, Dimitrova, Adámek, Bílková and Böhm2020; Coosemans, Dekeyser & Baelmans Reference Coosemans, Dekeyser and Baelmans2020, Reference Coosemans, Dekeyser and Baelmans2021b, Reference Coosemans, Dekeyser and Baelmans2022; Coosemans Reference Coosemans2022; Dekeyser et al. Reference Dekeyser, Coosemans, Carli and Baelmans2022). These characteristics of the turbulence (turbulent kinetic energy, possibly turbulent enstrophy or turbulent kinetic energy dissipation) are obtained self-consistently by solving additional mean-field equations for these quantities. In general, these additional mean-field transport equations, in turn, contain a number of closure terms. While the degree of realism used in modelling these equations differs between the cited references, an ad hoc phenomenological description is often used.
Coosemans et al. (Reference Coosemans, Dekeyser and Baelmans2020, Reference Coosemans, Dekeyser and Baelmans2021b, Reference Coosemans, Dekeyser and Baelmans2022) started the modelling of the turbulent kinetic energy ($k_{\perp }$![]() ) and enstrophy ($\zeta _{\perp }$
) and enstrophy ($\zeta _{\perp }$![]() ) from the analytical transport equations for these quantities derived there. However, these analytical equations are only strictly valid for the simplified case of two-dimensional (2-D) interchange-dominated, electrostatic, $E\times B$
) from the analytical transport equations for these quantities derived there. However, these analytical equations are only strictly valid for the simplified case of two-dimensional (2-D) interchange-dominated, electrostatic, $E\times B$![]() -only turbulence in the scrape-off layer (SOL) studied there. For a more general case, Scott (Reference Scott2003) derived mean-field energy equations already. The current paper revisits these derivations, while improving on the exact definition of the averaging operators and retaining a number of additional terms. Furthermore, these equations will be extended to provide equations for the kinetic energy in the $E\times B$
-only turbulence in the scrape-off layer (SOL) studied there. For a more general case, Scott (Reference Scott2003) derived mean-field energy equations already. The current paper revisits these derivations, while improving on the exact definition of the averaging operators and retaining a number of additional terms. Furthermore, these equations will be extended to provide equations for the kinetic energy in the $E\times B$![]() velocity fluctuations specifically. Given that mainly the turbulent $E\times B$
velocity fluctuations specifically. Given that mainly the turbulent $E\times B$![]() fluxes need to be modelled, this quantity is expected to be of particular relevance.
fluxes need to be modelled, this quantity is expected to be of particular relevance.
The remainder of this paper is organised as follows. First, § 2 presents the instantaneous (fluid) equations describing the $E\times B$![]() -dominated drift turbulence in the plasma edge. Next, § 3 describes a rigorous averaging procedure and applies this to the turbulent equations to derive mean-field equations describing the average transport. This identifies the closure terms which are due to the turbulent fluctuations. To facilitate the understanding and modelling of these closure terms, § 4 presents analytical transport equations for the various energy forms in the plasma (thermal energy, perpendicular and parallel mean-field and turbulent kinetic energy and mean-field and fluctuating magnetic energy). Section 5 then zooms in on the kinetic energy in the $E\times B$
-dominated drift turbulence in the plasma edge. Next, § 3 describes a rigorous averaging procedure and applies this to the turbulent equations to derive mean-field equations describing the average transport. This identifies the closure terms which are due to the turbulent fluctuations. To facilitate the understanding and modelling of these closure terms, § 4 presents analytical transport equations for the various energy forms in the plasma (thermal energy, perpendicular and parallel mean-field and turbulent kinetic energy and mean-field and fluctuating magnetic energy). Section 5 then zooms in on the kinetic energy in the $E\times B$![]() velocity fluctuations in particular. Section 6 recapitulates the main steps taken to model the average $E\times B$
velocity fluctuations in particular. Section 6 recapitulates the main steps taken to model the average $E\times B$![]() turbulent transport in earlier publications and comments on future extensions based on the analytical framework presented in the present paper. Finally, § 7 summarises the main conclusion of this work.
turbulent transport in earlier publications and comments on future extensions based on the analytical framework presented in the present paper. Finally, § 7 summarises the main conclusion of this work.
2. Turbulence equations
This section presents the quasi-neutral fluid equations which describe the instantaneous dynamics of the plasma edge, incorporating in particular the dynamics of the turbulence. This fluid assumption is often made in plasma edge modelling (Ricci et al. Reference Ricci, Halpern, Jolliet, Loizu, Mosetto, Fasoli, Furno and Theiler2012; Halpern et al. Reference Halpern, Ricci, Jolliet, Loizu, Morales, Mosetto, Musil, Riva, Wersal and Tran2016; Tamain et al. Reference Tamain, Bufferand, Ciraolo, Colin, Galassi, Ghendrih, Schwander and Serre2016; Stegmeir et al. Reference Stegmeir, Ross, Body, Francisquez, Zholobenko, Coster, Maj, Manz, Jenko and Rogers2019; Bufferand et al. Reference Bufferand, Bucalossi, Ciraolo, Falchetto, Gallo, Ghendrih, Rivals, Tamain, Yang and Giorgiani2021) despite the fact that edge plasmas are in practice often just marginally collisional (Stangeby Reference Stangeby2000), limiting the strict validity of the fluid treatment. Even though these fluid equations are, in principle, well known in the community, we explicitly include them as they form the starting point for the following derivations. In particular, this is of interest for the different contributions to the polarisation current as it will be defined here. The ion continuity, electron continuity, ion thermal energy, electron thermal energy, ion momentum and electron momentum equations take the following form:
In these equations, $t$![]() is time, $n_i$
is time, $n_i$![]() and $n_e$
and $n_e$![]() the ion and electron particle densities, $\boldsymbol {V}$
the ion and electron particle densities, $\boldsymbol {V}$![]() and $\boldsymbol {V}_e$
and $\boldsymbol {V}_e$![]() the ion and electron velocities, $S_{n_{i}}$
the ion and electron velocities, $S_{n_{i}}$![]() and $S_{n_{e}}$
and $S_{n_{e}}$![]() the ion and electron particle sources, $p_{{i}}$
the ion and electron particle sources, $p_{{i}}$![]() and $p_{{e}}$
and $p_{{e}}$![]() the ion and electron pressures, $\boldsymbol {q}_i$
the ion and electron pressures, $\boldsymbol {q}_i$![]() and $\boldsymbol {q}_e$
and $\boldsymbol {q}_e$![]() the ion and electron conductive heat fluxes, $\boldsymbol{\varPi}$
the ion and electron conductive heat fluxes, $\boldsymbol{\varPi}$![]() the (ion) viscous stress tensor, $Q_{\mathrm {ei}}$
the (ion) viscous stress tensor, $Q_{\mathrm {ei}}$![]() the electron–ion heat exchange, $S_{H,i}$
the electron–ion heat exchange, $S_{H,i}$![]() and $S_{H,e}$
and $S_{H,e}$![]() the ion and electron heat sources, $\boldsymbol {J}$
the ion and electron heat sources, $\boldsymbol {J}$![]() the current density, $\boldsymbol {R}_{{\rm ei}}$
the current density, $\boldsymbol {R}_{{\rm ei}}$![]() the electron–ion friction force, $m$
the electron–ion friction force, $m$![]() the ion mass, $e$
the ion mass, $e$![]() the electron charge, $\boldsymbol {E}$
the electron charge, $\boldsymbol {E}$![]() the electric field, $\boldsymbol {B}$
the electric field, $\boldsymbol {B}$![]() the magnetic field and $\boldsymbol {S}_{m}$
the magnetic field and $\boldsymbol {S}_{m}$![]() the (ion) momentum source. In this manuscript we consider plasmas consisting of only a single hydrogen isotope ($Z_i=1$
the (ion) momentum source. In this manuscript we consider plasmas consisting of only a single hydrogen isotope ($Z_i=1$![]() ) such that $n=n_i=n_e$
) such that $n=n_i=n_e$![]() and $\boldsymbol {J}=en(\boldsymbol {V}-\boldsymbol {V}_e)$
and $\boldsymbol {J}=en(\boldsymbol {V}-\boldsymbol {V}_e)$![]() . Hence, only one continuity equation, (2.1) or (2.2) needs to be used, not both. Furthermore, the electron inertia is neglected.
. Hence, only one continuity equation, (2.1) or (2.2) needs to be used, not both. Furthermore, the electron inertia is neglected.
Direct numerical solution of (2.1)–(2.6) is very difficult, in particular for the perpendicular components of the ion momentum equation (2.5) which are strongly dominated by the force terms on the right-hand side, with the inertial terms on the left-hand side being much smaller. In order to arrive at a more workable equation set, the equations are typically rewritten in such a way that the fluxes parallel to the magnetic field (in the magnetic field direction $\boldsymbol {b}=\boldsymbol {B}/B$![]() ) and the fluxes perpendicular to it are decoupled. Taking the cross-product of $\boldsymbol {B}$
) and the fluxes perpendicular to it are decoupled. Taking the cross-product of $\boldsymbol {B}$![]() with the momentum equations (2.5) and (2.6) and rewriting yields expressions for the perpendicular components of the ion and electron fluxes. The difference between both provides an expression for the perpendicular plasma current
with the momentum equations (2.5) and (2.6) and rewriting yields expressions for the perpendicular components of the ion and electron fluxes. The difference between both provides an expression for the perpendicular plasma current



In these expressions, we defined the ion particle flux perpendicular to the magnetic field $\boldsymbol {\varGamma }_{\perp,i}$![]() , the polarisation velocity $\boldsymbol {V}_{p}=\boldsymbol {V}_{p,0}+\boldsymbol {V}_{p,\varPi }$
, the polarisation velocity $\boldsymbol {V}_{p}=\boldsymbol {V}_{p,0}+\boldsymbol {V}_{p,\varPi }$![]() , the ion and electron diamagnetic velocities $\boldsymbol {V}_{*,i}$
, the ion and electron diamagnetic velocities $\boldsymbol {V}_{*,i}$![]() and $\boldsymbol {V}_{*,e}$
and $\boldsymbol {V}_{*,e}$![]() , the $E\times B$
, the $E\times B$![]() velocity $\boldsymbol {V}_{E}$
velocity $\boldsymbol {V}_{E}$![]() , the current perpendicular to the magnetic field $\boldsymbol {J}_{\perp }$
, the current perpendicular to the magnetic field $\boldsymbol {J}_{\perp }$![]() , the polarisation current $\boldsymbol {J}_{p}=\boldsymbol {J}_{p,0}+\boldsymbol {J}_{p,\varPi }$
, the polarisation current $\boldsymbol {J}_{p}=\boldsymbol {J}_{p,0}+\boldsymbol {J}_{p,\varPi }$![]() and the diamagnetic current $\boldsymbol {J}_{*}$
and the diamagnetic current $\boldsymbol {J}_{*}$![]() as indicated. In these equations, the total particle flux is decomposed in a parallel and a perpendicular component as $\boldsymbol {\varGamma }=\boldsymbol {\varGamma }_{\|}+\boldsymbol {\varGamma }_{\perp }$
as indicated. In these equations, the total particle flux is decomposed in a parallel and a perpendicular component as $\boldsymbol {\varGamma }=\boldsymbol {\varGamma }_{\|}+\boldsymbol {\varGamma }_{\perp }$![]() , where $\boldsymbol {\varGamma }_{\|}\triangleq (\boldsymbol {\varGamma }\boldsymbol {\cdot }\boldsymbol {b})\boldsymbol {b}$
, where $\boldsymbol {\varGamma }_{\|}\triangleq (\boldsymbol {\varGamma }\boldsymbol {\cdot }\boldsymbol {b})\boldsymbol {b}$![]() and $\boldsymbol {\varGamma }_{\perp }\triangleq -\boldsymbol {b}\times (\boldsymbol {b}\times \boldsymbol {\varGamma })$
and $\boldsymbol {\varGamma }_{\perp }\triangleq -\boldsymbol {b}\times (\boldsymbol {b}\times \boldsymbol {\varGamma })$![]() . Note that we use bold symbols to represent vectors, while non-bold symbols are scalars. In particular, the parallel component of a vector is denoted with a subscript $\|$
. Note that we use bold symbols to represent vectors, while non-bold symbols are scalars. In particular, the parallel component of a vector is denoted with a subscript $\|$![]() , e.g. $\boldsymbol {V}_{\|}=\it{V}_{\|}\boldsymbol {b}$
, e.g. $\boldsymbol {V}_{\|}=\it{V}_{\|}\boldsymbol {b}$![]() . Later on, we will use the symbol $\nabla_{\|}=\boldsymbol {b}\boldsymbol {\cdot }\boldsymbol {\nabla }$
. Later on, we will use the symbol $\nabla_{\|}=\boldsymbol {b}\boldsymbol {\cdot }\boldsymbol {\nabla }$![]() as a scalar parallel gradient operator. The $\boldsymbol {\nabla }_{\perp }$
as a scalar parallel gradient operator. The $\boldsymbol {\nabla }_{\perp }$![]() operator is considered a vector operator of course, i.e. $\boldsymbol {\nabla }_{\perp }=\boldsymbol {\nabla }-\boldsymbol {b}\nabla_{\|}$
operator is considered a vector operator of course, i.e. $\boldsymbol {\nabla }_{\perp }=\boldsymbol {\nabla }-\boldsymbol {b}\nabla_{\|}$![]() . Using these conventions, we can for example write $\boldsymbol {V}_{\|}\boldsymbol {\cdot }\boldsymbol {\nabla } p=V_{\|}\nabla_{\|} p$
. Using these conventions, we can for example write $\boldsymbol {V}_{\|}\boldsymbol {\cdot }\boldsymbol {\nabla } p=V_{\|}\nabla_{\|} p$![]() or $\boldsymbol {A}_{\|}\boldsymbol {\cdot }\boldsymbol {J}_{\|}=\it{A}_{\|}J_{\|}$
or $\boldsymbol {A}_{\|}\boldsymbol {\cdot }\boldsymbol {J}_{\|}=\it{A}_{\|}J_{\|}$![]() without loss of generality.
without loss of generality.
A rigorous ordering of the drift terms in (2.7)–(2.9) shows that the $E\times B$![]() and diamagnetic drifts are typically the dominant terms, while the polarisation drift is of higher order (Goldston & Rutherford Reference Goldston and Rutherford1995; Simakov & Catto Reference Simakov and Catto2004; Fundamenski Reference Fundamenski2010). Moreover, we will neglect the perpendicular contributions to the electron–ion friction $\boldsymbol {R}_{{\rm ei}}$
and diamagnetic drifts are typically the dominant terms, while the polarisation drift is of higher order (Goldston & Rutherford Reference Goldston and Rutherford1995; Simakov & Catto Reference Simakov and Catto2004; Fundamenski Reference Fundamenski2010). Moreover, we will neglect the perpendicular contributions to the electron–ion friction $\boldsymbol {R}_{{\rm ei}}$![]() and thus the corresponding drifts altogether from this point on. Hence, we consider the velocity
and thus the corresponding drifts altogether from this point on. Hence, we consider the velocity
the dominant contribution to the plasma (ion) momentum (the electron momentum having been neglected from the start).
In view of later derivations, we will henceforth distinguish the velocity used in the ion convection operators and the velocity considered for the inertia. For this reason, we define the symbol $\boldsymbol {V}_{C}$![]() for the ion convective velocity and avoid writing specific velocity components for it in the plasma momentum equations (charge balance and plasma parallel momentum). It will be assumed that the ion convective velocity $\boldsymbol {V}_{C}$
for the ion convective velocity and avoid writing specific velocity components for it in the plasma momentum equations (charge balance and plasma parallel momentum). It will be assumed that the ion convective velocity $\boldsymbol {V}_{C}$![]() is the same in the plasma momentum equations and in the ion continuity equation, as should be the case in theory. For reasons of energetic consistency, this implies $\boldsymbol {V}_{C}=\boldsymbol {V}_0+\boldsymbol {V}_{p}$
is the same in the plasma momentum equations and in the ion continuity equation, as should be the case in theory. For reasons of energetic consistency, this implies $\boldsymbol {V}_{C}=\boldsymbol {V}_0+\boldsymbol {V}_{p}$![]() . Note that we will not explicitly make use of the so-called ‘gyro-viscous cancellation’ in this paper; this cancellation is not used in the charge balance equation (2.20) (in the definition of $\boldsymbol {J}_{p}$
. Note that we will not explicitly make use of the so-called ‘gyro-viscous cancellation’ in this paper; this cancellation is not used in the charge balance equation (2.20) (in the definition of $\boldsymbol {J}_{p}$![]() ) nor in the parallel momentum equation (2.23). This would allow cancelling part of the viscous stress tensor $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol{\varPi}$
) nor in the parallel momentum equation (2.23). This would allow cancelling part of the viscous stress tensor $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol{\varPi}$![]() with a part of the momentum transport (approximately $\boldsymbol {\nabla }\boldsymbol {\cdot } mn\boldsymbol {V}_{*,i}\boldsymbol {V}_0$
with a part of the momentum transport (approximately $\boldsymbol {\nabla }\boldsymbol {\cdot } mn\boldsymbol {V}_{*,i}\boldsymbol {V}_0$![]() ). The details of this cancellation remain a topic of study in the community (Rognlien et al. Reference Rognlien, Ryutov, Mattor and Porter1999; Rozhansky et al. Reference Rozhansky, Voskoboynikov, Kaveeva, Coster and Schneider2001; Ramos Reference Ramos2005). As such, the stress tensor $\boldsymbol{\varPi}$
). The details of this cancellation remain a topic of study in the community (Rognlien et al. Reference Rognlien, Ryutov, Mattor and Porter1999; Rozhansky et al. Reference Rozhansky, Voskoboynikov, Kaveeva, Coster and Schneider2001; Ramos Reference Ramos2005). As such, the stress tensor $\boldsymbol{\varPi}$![]() represents the full Braginskii stress tensor and the convective velocity $\boldsymbol {V}_{C}$
represents the full Braginskii stress tensor and the convective velocity $\boldsymbol {V}_{C}$![]() includes the diamagnetic velocity $\boldsymbol {V}_{*,i}$
includes the diamagnetic velocity $\boldsymbol {V}_{*,i}$![]() . The separate notation for the convective and inertial velocities might, however, facilitate subsequent derivations making use of the gyro-viscous cancellation in future work.
. The separate notation for the convective and inertial velocities might, however, facilitate subsequent derivations making use of the gyro-viscous cancellation in future work.
Assuming $\boldsymbol {V}_0$![]() is the dominant velocity for the inertia and writing $\boldsymbol {V}_{C}$
is the dominant velocity for the inertia and writing $\boldsymbol {V}_{C}$![]() for the convective velocity, the inertial contribution to the polarisation velocity can thus be written as
for the convective velocity, the inertial contribution to the polarisation velocity can thus be written as

where we introduced the notation
For future reference, we already decompose this inertial contribution to the polarisation current as
with


In the latter equations, we used the notation
A priori, it could be expected that the ${\rm D}\boldsymbol {b}/{\rm D} t$![]() terms in $\boldsymbol {J}_{p,E}$
terms in $\boldsymbol {J}_{p,E}$![]() and $\boldsymbol {J}_{p,*}$
and $\boldsymbol {J}_{p,*}$![]() provide but a small correction because of the limited changes in time and space of the magnetic field direction $\boldsymbol {b}$
provide but a small correction because of the limited changes in time and space of the magnetic field direction $\boldsymbol {b}$![]() . On the other hand, it could be imagined that $\boldsymbol {J}_{p,\|}$
. On the other hand, it could be imagined that $\boldsymbol {J}_{p,\|}$![]() does have a certain relevance as it also contains the large parallel velocity component; $\boldsymbol {J}_{p,\|}$
does have a certain relevance as it also contains the large parallel velocity component; $\boldsymbol {J}_{p,\|}$![]() will moreover be shown to lead to specific coupling terms in the perpendicular kinetic energy equation, see §§ 4.1, 5.1 and 5.2.
will moreover be shown to lead to specific coupling terms in the perpendicular kinetic energy equation, see §§ 4.1, 5.1 and 5.2.
As the $E\times B$![]() drift velocity is of prime importance in the perpendicular direction, the treatment of the magnetic field and the electric field are crucial. From the drift hydrodynamic (DHD) description (Fundamenski Reference Fundamenski2010) and/or the low $\beta$
drift velocity is of prime importance in the perpendicular direction, the treatment of the magnetic field and the electric field are crucial. From the drift hydrodynamic (DHD) description (Fundamenski Reference Fundamenski2010) and/or the low $\beta$![]() assumption, it follows that the externally imposed magnetic field (i.e. by the toroidal field coils and the plasma current in the core) far exceeds the magnetic field fluctuations generated by electromagnetic effects in the plasma edge. For these reasons, the magnetic field $\boldsymbol {B}$
assumption, it follows that the externally imposed magnetic field (i.e. by the toroidal field coils and the plasma current in the core) far exceeds the magnetic field fluctuations generated by electromagnetic effects in the plasma edge. For these reasons, the magnetic field $\boldsymbol {B}$![]() will be assumed to be constant in time and externally imposed (with the exception of its treatment in the parallel electric field). The net transport as a result of magnetic field lines fluctuating around their equilibrium position (magnetic flutter transport) is neglected in this work.
will be assumed to be constant in time and externally imposed (with the exception of its treatment in the parallel electric field). The net transport as a result of magnetic field lines fluctuating around their equilibrium position (magnetic flutter transport) is neglected in this work.
We then write the electric field as
In this equation $\phi$![]() is the electrostatic potential and $\boldsymbol {A}_{\|}$
is the electrostatic potential and $\boldsymbol {A}_{\|}$![]() is the parallel component of the magnetic vector potential $\boldsymbol {A}$
is the parallel component of the magnetic vector potential $\boldsymbol {A}$![]() defined as $\boldsymbol {B}\triangleq \boldsymbol {\nabla }\times \boldsymbol {A}$
defined as $\boldsymbol {B}\triangleq \boldsymbol {\nabla }\times \boldsymbol {A}$![]() with $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {A} \triangleq 0$
with $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {A} \triangleq 0$![]() . The electrostatic contribution to the electric field is widely accepted to be dominant in the plasma edge, and the electromagnetic contribution is often neglected (low $\beta$
. The electrostatic contribution to the electric field is widely accepted to be dominant in the plasma edge, and the electromagnetic contribution is often neglected (low $\beta$![]() ). The parallel magnetic vector potential $\boldsymbol {A}_{\|}$
). The parallel magnetic vector potential $\boldsymbol {A}_{\|}$![]() is retained, however, since the literature indicates it may play a role in the dynamics of the turbulence in the plasma edge through its influence on the drift-wave coupling (see § 4) (Scott Reference Scott2003, Reference Scott2005; Ribeiro & Scott Reference Ribeiro and Scott2005; Fundamenski Reference Fundamenski2010). Furthermore, this term is also responsible for inducing a loop voltage in the tokamak through the transformer action of the central solenoid. The contribution of $\boldsymbol {A}_{\perp }$
is retained, however, since the literature indicates it may play a role in the dynamics of the turbulence in the plasma edge through its influence on the drift-wave coupling (see § 4) (Scott Reference Scott2003, Reference Scott2005; Ribeiro & Scott Reference Ribeiro and Scott2005; Fundamenski Reference Fundamenski2010). Furthermore, this term is also responsible for inducing a loop voltage in the tokamak through the transformer action of the central solenoid. The contribution of $\boldsymbol {A}_{\perp }$![]() is neglected because it is found to be small for the rather slow time scales assumed in the DHD ordering (Simakov & Catto Reference Simakov and Catto2004; Fundamenski Reference Fundamenski2010).
is neglected because it is found to be small for the rather slow time scales assumed in the DHD ordering (Simakov & Catto Reference Simakov and Catto2004; Fundamenski Reference Fundamenski2010).
Note that, whether the parallel magnetic vector potential is taken into account or not, the $E\times B$![]() velocity can be written as
velocity can be written as
and is thus determined by the electrostatic potential (and the magnetic field that is assumed to be constant in time in this expression, i.e. without influence of $\boldsymbol {A}_{\|}$![]() ). Then, an equation for the electrostatic potential is still needed to be able to calculate the $E\times B$
). Then, an equation for the electrostatic potential is still needed to be able to calculate the $E\times B$![]() velocity. Since the plasma is assumed to be quasi-neutral, the net space charge is zero and Gauss’ law cannot be used. Instead, the charge balance condition $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {J}=0$
velocity. Since the plasma is assumed to be quasi-neutral, the net space charge is zero and Gauss’ law cannot be used. Instead, the charge balance condition $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {J}=0$![]() , which maintains the neutrality of the plasma, provides an equation for the electrostatic potential. Note that this expression can be derived by combining the ion and electron continuity equations (2.1)–(2.2) under quasineutrality. Using expression (2.9), this charge balance equation can be rewritten as
, which maintains the neutrality of the plasma, provides an equation for the electrostatic potential. Note that this expression can be derived by combining the ion and electron continuity equations (2.1)–(2.2) under quasineutrality. Using expression (2.9), this charge balance equation can be rewritten as
The parallel magnetic vector potential $A_{\|}$![]() can be calculated from the projection of the electron momentum equation (2.6) on the parallel direction $\boldsymbol {b}$
can be calculated from the projection of the electron momentum equation (2.6) on the parallel direction $\boldsymbol {b}$![]()
In this above equation, which is also referred to as ‘Ohm's law’, the Braginskii closure for the parallel friction force $\it{R}_{ei,\|}=\boldsymbol {R}_{{\rm ei}}\boldsymbol {\cdot }\boldsymbol {b}=en\eta _{\|}J_{\|}-{\rm 0.71}n\nabla_{\|} T_e$![]() is used. The parallel current density is then calculated using the equation
is used. The parallel current density is then calculated using the equation
stemming from Ampère's law. Note that, in the fully electrostatic case, i.e. $\partial \boldsymbol {A}_{\|}/\partial t=0$![]() , (2.21) can just be solved for $\boldsymbol {J}_{\|}$
, (2.21) can just be solved for $\boldsymbol {J}_{\|}$![]() .
.
Finally, the parallel ion velocity is solved from projecting the total plasma momentum equation (the sum of the ion and electron momentum equations (2.5) and (2.6)) on the parallel direction
The third term on the right-hand side of this equation enters due to changes in time or in space of the magnetic field direction. Note that this term is simplified as ${{\rm D}\boldsymbol {b}}/{{\rm D} t}\boldsymbol {\cdot }\boldsymbol {V}_0={{\rm D}\boldsymbol {b}}/{{\rm D} t}\boldsymbol {\cdot }\boldsymbol {V}_{0,\perp }$![]() since ${{\rm D}\boldsymbol {b}}/{{\rm D} t}\boldsymbol {\cdot }\boldsymbol {b}=0$
since ${{\rm D}\boldsymbol {b}}/{{\rm D} t}\boldsymbol {\cdot }\boldsymbol {b}=0$![]() for the unit vector $\boldsymbol {b}$
for the unit vector $\boldsymbol {b}$![]() .
.
To summarise, the drift-reduced equations to be solved are the continuity equation for ions or electrons (2.1) or (2.2), the thermal energy equations for ions (2.3) and electrons (2.4), the parallel momentum equations for the electrons and for the plasma as a whole (2.21) and (2.23), the charge balance equation (2.20) and Ampère's law (2.22). In all these equations, the dominant perpendicular drift velocities and currents in expressions (2.7)–(2.9) can be filled out where appropriate. If electromagnetic effects are ignored, (2.21) is solved for the parallel current $\boldsymbol {J}_{\|}$![]() and (2.22) is obsolete. Finally, expressions for the sources $S_{n}$
and (2.22) is obsolete. Finally, expressions for the sources $S_{n}$![]() , $\boldsymbol {S}_{m}$
, $\boldsymbol {S}_{m}$![]() , $S_{H,i}$
, $S_{H,i}$![]() , $S_{H,e}$
, $S_{H,e}$![]() , the viscous stress $\boldsymbol{\varPi}$
, the viscous stress $\boldsymbol{\varPi}$![]() , the friction force $R_{{\rm ei}}$
, the friction force $R_{{\rm ei}}$![]() , the heat fluxes $\boldsymbol {q}_i$
, the heat fluxes $\boldsymbol {q}_i$![]() and $\boldsymbol {q}_e$
and $\boldsymbol {q}_e$![]() and the electron–ion heat exchange $Q_{{\rm ei}}$
and the electron–ion heat exchange $Q_{{\rm ei}}$![]() are still required. Such expressions can be found for example in Braginskii (Reference Braginskii1965) and Fundamenski (Reference Fundamenski2010).
are still required. Such expressions can be found for example in Braginskii (Reference Braginskii1965) and Fundamenski (Reference Fundamenski2010).
3. Basic mean-field equations
In the previous section, the fluid equations describing the instantaneous dynamics of the edge plasma have been presented. These equations tend to develop a chaotic, turbulent flow with large fluctuations. In general, it is rather the average behaviour of the turbulence and the resulting average profiles of density and pressure that are of interest. However, the turbulent fluctuations introduce a number of closure terms in the mean-field equations which need to be modelled. Typically, the treatment of these closure terms in mean-field codes is minimal and very ad hoc. The current approach in mean-field modelling is basically to take the full turbulence equations from the previous section and to evaluate them with mean-field quantities. In addition to this, ad hoc diffusion (or sometimes advection) terms are added to model the average radial turbulent transport. Due to turbulent fluctuations, these equations are not equivalent to the turbulent equations and forego the actual dynamics of the turbulence. As a contribution of this paper, this section derives mean-field equations that do correspond to the underlying turbulence equations analytically through a rigorous averaging methodology. The resulting equations will give more insight into which terms are being modelled and/or neglected in the mean-field codes. Furthermore, this will allow to evaluate the terms to be modelled using reference data. The methodology followed for analytically deriving these mean-field equations is inspired by Scott (Reference Scott2003).
In order to derive the averaged, mean-field equations, all quantities are split in a mean-field component and a fluctuating component, as is done in the Reynolds-Averaged Navier–Stokes (RANS) methodology for hydrodynamic turbulence. Both the Reynolds and the Favre decomposition of turbulent quantities will be used. The Reynolds decomposition of a general quantity $u$![]() is (Pope Reference Pope2015)
is (Pope Reference Pope2015)

In this work, we assume the turbulent flows to be ergodic such that a long time statistical steady state of the flow exists, of which the time average converges to the ensemble average

In this definition, $u^{(i)}$![]() is the value that the quantity $u$
is the value that the quantity $u$![]() would take (at a given time and position) in the $i$
would take (at a given time and position) in the $i$![]() th (hypothetical) realisation of the same flow conditions. Due to the stochastic nature of turbulence, if the same conditions were created $N$
th (hypothetical) realisation of the same flow conditions. Due to the stochastic nature of turbulence, if the same conditions were created $N$![]() times, the (details of the) resulting flow would nonetheless be different every time. Here, an average is taken over $N$
times, the (details of the) resulting flow would nonetheless be different every time. Here, an average is taken over $N$![]() such ‘realisations’ in the limit of $N$
such ‘realisations’ in the limit of $N$![]() going to infinity. In addition to the Reynolds average, the Favre or density weighted average will also be used. This is defined as follows (Canuto Reference Canuto1997):
going to infinity. In addition to the Reynolds average, the Favre or density weighted average will also be used. This is defined as follows (Canuto Reference Canuto1997):
This Favre average is particularly useful when transport equations with variable density need to be averaged, as it allows us to limit the number of closure terms in that case. Held et al. (Reference Held, Wiesenberger, Kube and Kendl2018) and Wiesenberger & Held (Reference Wiesenberger and Held2020) have for example used such Favre averaging techniques to account for the effect of density fluctuations in the study of zonal flow and angular momentum generation.
As discussed in the previous section, this paper only considers low $\beta$![]() plasmas. Hence, it is assumed that strong time-constant magnetic fields are externally applied and that fluctuations of the magnetic field can be neglected. As such, the magnetic fields can be brought out of the averaging operators. An exception to this is again the treatment of $\it{A}_{\|}$
plasmas. Hence, it is assumed that strong time-constant magnetic fields are externally applied and that fluctuations of the magnetic field can be neglected. As such, the magnetic fields can be brought out of the averaging operators. An exception to this is again the treatment of $\it{A}_{\|}$![]() in the parallel momentum equations.
in the parallel momentum equations.
Reynolds averaging, i.e. applying the ensemble average operator defined in (3.2) to the continuity equations (2.1) and (2.2), the thermal energy equations (2.3) and (2.4), the parallel momentum equations (2.21) and (2.23) the charge balance equation (2.20) and Ampère's law (2.22), the following mean-field equations are obtained:




Note that, while the ensemble averaging operation used to derive these equations is unambiguously defined, the use of either a Reynolds or a Favre decomposition for each of the quantities in the equations is a choice. In making this choice (here and further on in this manuscript), we have generally been guided by an attempt to minimise the number of closure terms, and by considerations related to the numerical strategies typically used to solve these equations. We will come back to some of these choices later on. In (3.6)–(3.13), we used the following notation:

In (3.6)–(3.9) the convective velocities have explicitly been filled out on the left-hand side to highlight the turbulent fluxes. In principle, this could also be done for the momentum equations (3.11) and (3.12).
In (3.8) and (3.9), it was assumed that the only important conductive heat fluxes are the parallel ones $\boldsymbol {q}_{\|}$![]() and the one due to the diamagnetic drift. The latter is combined with the diamagnetic heat convection to obtain the one but last term on the left-hand side of (3.8) and (3.9) (Scott Reference Scott2003). The pressure work on the diamagnetic velocity is $\boldsymbol {\nabla } p\boldsymbol {\cdot }\boldsymbol {V}_{*} \equiv 0$
and the one due to the diamagnetic drift. The latter is combined with the diamagnetic heat convection to obtain the one but last term on the left-hand side of (3.8) and (3.9) (Scott Reference Scott2003). The pressure work on the diamagnetic velocity is $\boldsymbol {\nabla } p\boldsymbol {\cdot }\boldsymbol {V}_{*} \equiv 0$![]() .
.
In theory, this system of equations could be used to obtain the following mean-field quantities. The continuity equation (3.6) or 3.7 is to be solved for the average density $\bar {n}$![]() (as mentioned in § 2 already it suffices to solve one of both for a quasi-neutral single species hydrogenic plasma in which $n=n_{e}=n_{i}$
(as mentioned in § 2 already it suffices to solve one of both for a quasi-neutral single species hydrogenic plasma in which $n=n_{e}=n_{i}$![]() ), the mean-field thermal energy equations (3.8) and (3.9) for the average pressures $\bar {p}_i$
), the mean-field thermal energy equations (3.8) and (3.9) for the average pressures $\bar {p}_i$![]() and $\bar {p}_e$
and $\bar {p}_e$![]() (which allows calculating the Favre-averaged temperatures $\tilde {T}_i=\bar {p}_i/\bar {n}$
(which allows calculating the Favre-averaged temperatures $\tilde {T}_i=\bar {p}_i/\bar {n}$![]() and $\tilde {T}_e=\bar {p}_e/\bar {n}$
and $\tilde {T}_e=\bar {p}_e/\bar {n}$![]() ) and the mean-field plasma parallel momentum equation (3.11) for the Favre-averaged parallel ion velocity $\tilde {V}_{\|}$
) and the mean-field plasma parallel momentum equation (3.11) for the Favre-averaged parallel ion velocity $\tilde {V}_{\|}$![]() . The mean-field Ohm's law 3.10 is solved for $\bar {A}_{\|}$
. The mean-field Ohm's law 3.10 is solved for $\bar {A}_{\|}$![]() , which then yields $\bar {J}_{\|}$
, which then yields $\bar {J}_{\|}$![]() through (3.13). Through the dependence of $\boldsymbol {U}_0$
through (3.13). Through the dependence of $\boldsymbol {U}_0$![]() on $\phi$
on $\phi$![]() (see (2.12a,b)), the mean-field charge balance equation (3.12) is then solved for the average potential $\bar {\phi }$
(see (2.12a,b)), the mean-field charge balance equation (3.12) is then solved for the average potential $\bar {\phi }$![]() . However, a whole number of closure terms arise in (3.6)–(3.13) when averaging the nonlinear terms. Any of the terms in the equations (above and later on in this manuscript) that feature Reynolds fluctuations (e.g. $\phi '$
. However, a whole number of closure terms arise in (3.6)–(3.13) when averaging the nonlinear terms. Any of the terms in the equations (above and later on in this manuscript) that feature Reynolds fluctuations (e.g. $\phi '$![]() ), Favre fluctuations (e.g. $V_E''$
), Favre fluctuations (e.g. $V_E''$![]() ) or any other averaged nonlinear term that cannot be expressed in terms of the resolved mean-field quantities (e.g. $\overline {V_{\|}\nabla_{\|} p}$
) or any other averaged nonlinear term that cannot be expressed in terms of the resolved mean-field quantities (e.g. $\overline {V_{\|}\nabla_{\|} p}$![]() ) forms a closure term. These closure terms depend on the correlation between fluctuations and cannot directly be determined based on the ‘given’ mean-field quantities only. As such, solving these equations is not as simple as that since the equation set is not closed. On another note, we remark that the $\partial \bar {A}_{\|}/\partial t$
) forms a closure term. These closure terms depend on the correlation between fluctuations and cannot directly be determined based on the ‘given’ mean-field quantities only. As such, solving these equations is not as simple as that since the equation set is not closed. On another note, we remark that the $\partial \bar {A}_{\|}/\partial t$![]() term in the electron momentum equation (3.10) is typically neglected in both turbulence codes and mean-field codes. In stationary tokamak operation, this term would ideally be constant (i.e. $\bar {A}_{\|}$
term in the electron momentum equation (3.10) is typically neglected in both turbulence codes and mean-field codes. In stationary tokamak operation, this term would ideally be constant (i.e. $\bar {A}_{\|}$![]() increasing linearly in time) to maintain a constant loop voltage, while the average magnetic field ($\bar {\boldsymbol {B}}=\boldsymbol {\nabla } \times \bar {\boldsymbol {A}}$
increasing linearly in time) to maintain a constant loop voltage, while the average magnetic field ($\bar {\boldsymbol {B}}=\boldsymbol {\nabla } \times \bar {\boldsymbol {A}}$![]() ) is maintained constant in time.
) is maintained constant in time.
In this article, we focus on modelling the turbulent $E\times B$![]() particle flux $\boldsymbol {\varGamma }_{n,t,E}$
particle flux $\boldsymbol {\varGamma }_{n,t,E}$![]() (see (3.15a–c)) and the turbulent $E\times B$
(see (3.15a–c)) and the turbulent $E\times B$![]() heat fluxes $\boldsymbol {\varGamma }_{\textrm {pi}/e,E}$
heat fluxes $\boldsymbol {\varGamma }_{\textrm {pi}/e,E}$![]() (see (3.18a–c)) since these are known to dominate the outward transport of particles and heat across magnetic flux surfaces in the plasma edge (Scott Reference Scott2003; Wesson Reference Wesson2004; Fundamenski Reference Fundamenski2010). The divergence of the diamagnetic fluxes of particles ($\boldsymbol {\varGamma }_{n,*,i/e}$
(see (3.18a–c)) since these are known to dominate the outward transport of particles and heat across magnetic flux surfaces in the plasma edge (Scott Reference Scott2003; Wesson Reference Wesson2004; Fundamenski Reference Fundamenski2010). The divergence of the diamagnetic fluxes of particles ($\boldsymbol {\varGamma }_{n,*,i/e}$![]() ) and thermal energy (penultimate term on the left-hand side of (3.8) and (3.9)) can be shown to be proportional to gradients of the magnetic field strengthFootnote 1. As the length scale of magnetic field strength variations in the plasma edge is typically large, these terms are expected to be rather small (Tsai et al. Reference Tsai, Perkins and Stix1970; Scott Reference Scott2007). Moreover, (3.16a–c) shows that the diamagnetic particle fluxes are not really closure terms since they can be calculated exactly from the mean-field pressures, which are available from thermal energy equations (3.8) and (3.9). The (ion) particle and (ion) thermal energy fluxes ($\boldsymbol {\varGamma }_{n,p}$
) and thermal energy (penultimate term on the left-hand side of (3.8) and (3.9)) can be shown to be proportional to gradients of the magnetic field strengthFootnote 1. As the length scale of magnetic field strength variations in the plasma edge is typically large, these terms are expected to be rather small (Tsai et al. Reference Tsai, Perkins and Stix1970; Scott Reference Scott2007). Moreover, (3.16a–c) shows that the diamagnetic particle fluxes are not really closure terms since they can be calculated exactly from the mean-field pressures, which are available from thermal energy equations (3.8) and (3.9). The (ion) particle and (ion) thermal energy fluxes ($\boldsymbol {\varGamma }_{n,p}$![]() and $\boldsymbol {\varGamma }_{p_{{i}},p}$
and $\boldsymbol {\varGamma }_{p_{{i}},p}$![]() ) due to the (ion) polarisation velocity $\boldsymbol {V}_{p}$
) due to the (ion) polarisation velocity $\boldsymbol {V}_{p}$![]() do entail a number of closure terms. However, since the polarisation velocity is of higher order than the other velocities in the continuity and thermal energy equations (Goldston & Rutherford Reference Goldston and Rutherford1995; Simakov & Catto Reference Simakov and Catto2004; Fundamenski Reference Fundamenski2010), its contribution can be assumed to be negligible in these equations. Finally, there are also parallel turbulent fluxes (see (3.19) and (3.20)). To the knowledge of the authors, these parallel turbulent heat fluxes are not included in mean-field transport codes and have not yet been addressed in literature. It is left for future work to carefully investigate whether they are indeed negligible compared with the large mean-field convective fluxes and the conductive heat flux $\boldsymbol {q}_{\|}$
do entail a number of closure terms. However, since the polarisation velocity is of higher order than the other velocities in the continuity and thermal energy equations (Goldston & Rutherford Reference Goldston and Rutherford1995; Simakov & Catto Reference Simakov and Catto2004; Fundamenski Reference Fundamenski2010), its contribution can be assumed to be negligible in these equations. Finally, there are also parallel turbulent fluxes (see (3.19) and (3.20)). To the knowledge of the authors, these parallel turbulent heat fluxes are not included in mean-field transport codes and have not yet been addressed in literature. It is left for future work to carefully investigate whether they are indeed negligible compared with the large mean-field convective fluxes and the conductive heat flux $\boldsymbol {q}_{\|}$![]() driven by fast classical collisional transport.
driven by fast classical collisional transport.
Note that all fluxes in expressions (3.14)–(3.21) except for the $E\times B$![]() particle flux are decomposed using Favre averages, which allows limiting the number of closure terms. For the $E\times B$
particle flux are decomposed using Favre averages, which allows limiting the number of closure terms. For the $E\times B$![]() drift, a similar Favre average does not make sense, since in mean-field modelling, the Reynolds average potential $\bar {\phi }$
drift, a similar Favre average does not make sense, since in mean-field modelling, the Reynolds average potential $\bar {\phi }$![]() is solved for from the average charge balance equation (3.12) and not the Favre-averaged potential. In this equation, the divergences of parallel current and diamagnetic current on the right-hand side are typically dominant, since the other terms are of higher order (Goldston & Rutherford Reference Goldston and Rutherford1995; Simakov & Catto Reference Simakov and Catto2004; Fundamenski Reference Fundamenski2010). As such, it is mostly important to treat the averages of these two terms with care. The average diamagnetic current $\overline {\boldsymbol {J}}_*=-\boldsymbol {\nabla }\bar {p}\times \boldsymbol {b}/B$
is solved for from the average charge balance equation (3.12) and not the Favre-averaged potential. In this equation, the divergences of parallel current and diamagnetic current on the right-hand side are typically dominant, since the other terms are of higher order (Goldston & Rutherford Reference Goldston and Rutherford1995; Simakov & Catto Reference Simakov and Catto2004; Fundamenski Reference Fundamenski2010). As such, it is mostly important to treat the averages of these two terms with care. The average diamagnetic current $\overline {\boldsymbol {J}}_*=-\boldsymbol {\nabla }\bar {p}\times \boldsymbol {b}/B$![]() does not lead to any closure terms. In Ohm's law (3.10) and Ampère's law (3.13), which together determine the parallel current, the Reynolds-averaged electrostatic potential $\bar {\phi }$
does not lead to any closure terms. In Ohm's law (3.10) and Ampère's law (3.13), which together determine the parallel current, the Reynolds-averaged electrostatic potential $\bar {\phi }$![]() appears naturally. Moreover, using $\bar {\phi }$
appears naturally. Moreover, using $\bar {\phi }$![]() allows us to obtain the three components of $\overline {\boldsymbol {\nabla }\phi }=\boldsymbol {\nabla }\bar {\phi }$
allows us to obtain the three components of $\overline {\boldsymbol {\nabla }\phi }=\boldsymbol {\nabla }\bar {\phi }$![]() with one scalar, while an alternative formulation in terms of $\widetilde {\boldsymbol {\nabla }\phi }\neq \boldsymbol {\nabla }\tilde {\phi }$
with one scalar, while an alternative formulation in terms of $\widetilde {\boldsymbol {\nabla }\phi }\neq \boldsymbol {\nabla }\tilde {\phi }$![]() would require modelling them separately. As a result, a Reynolds average is also used for the mean-field $E\times B$
would require modelling them separately. As a result, a Reynolds average is also used for the mean-field $E\times B$![]() drift i.e. $\bar {\boldsymbol {V}}_{E}=\boldsymbol {b}\times \boldsymbol {\nabla }\bar {\phi }/B$
drift i.e. $\bar {\boldsymbol {V}}_{E}=\boldsymbol {b}\times \boldsymbol {\nabla }\bar {\phi }/B$![]() and the $\overline {n'\boldsymbol {V}_{E}'}$
and the $\overline {n'\boldsymbol {V}_{E}'}$![]() closure for the $E\times B$
closure for the $E\times B$![]() flux is required in the average $E\times B$
flux is required in the average $E\times B$![]() particle flux in (3.15a–c). Note that, after modelling $\overline {n'\boldsymbol {V}_{E}'}$
particle flux in (3.15a–c). Note that, after modelling $\overline {n'\boldsymbol {V}_{E}'}$![]() , the Favre-averaged $E\times B$
, the Favre-averaged $E\times B$![]() velocity can be calculated as $\tilde {\boldsymbol {V}}_{E}=\bar {\boldsymbol {V}}_{E}+\overline {n'\boldsymbol {V}_{E}'}/\bar {n}$
velocity can be calculated as $\tilde {\boldsymbol {V}}_{E}=\bar {\boldsymbol {V}}_{E}+\overline {n'\boldsymbol {V}_{E}'}/\bar {n}$![]() . With these averaging choices, the left-hand side of (3.12) can thus be rewritten using the following identity:
. With these averaging choices, the left-hand side of (3.12) can thus be rewritten using the following identity:

Next to the turbulent fluxes of particles and heat, there are also turbulent momentum fluxes. These show up as the Reynolds stresses $m\overline {n\boldsymbol {V}_{C}''V_{\|}''}$![]() in the ion parallel momentum equation (3.11) and $m\overline {n\boldsymbol {V}_{C}''\boldsymbol {U}_0''}$
in the ion parallel momentum equation (3.11) and $m\overline {n\boldsymbol {V}_{C}''\boldsymbol {U}_0''}$![]() in the polarisation current in the charge balance equation (3.12) (or equivalently the terms in the last line of expression (3.22)). If desired, these fluxes could also be decomposed into different contributions due to the various velocities in $\boldsymbol {V}_{C}$
in the polarisation current in the charge balance equation (3.12) (or equivalently the terms in the last line of expression (3.22)). If desired, these fluxes could also be decomposed into different contributions due to the various velocities in $\boldsymbol {V}_{C}$![]() . Note that $\tilde {\boldsymbol {U}}_0$
. Note that $\tilde {\boldsymbol {U}}_0$![]() is not a (new) closure term in this equation, as it is equal to $\tilde {\boldsymbol {U}}_0 = (\tilde {\boldsymbol {V}}_{E}+\tilde {\boldsymbol {V}}_{*,i})\times \boldsymbol {b}$
is not a (new) closure term in this equation, as it is equal to $\tilde {\boldsymbol {U}}_0 = (\tilde {\boldsymbol {V}}_{E}+\tilde {\boldsymbol {V}}_{*,i})\times \boldsymbol {b}$![]() , where $\tilde {\boldsymbol {V}}_{E}$
, where $\tilde {\boldsymbol {V}}_{E}$![]() and $\tilde {\boldsymbol {V}}_{*,i}$
and $\tilde {\boldsymbol {V}}_{*,i}$![]() are known as soon as the perpendicular particle fluxes are modelled. On the other hand, (3.22) illustrates that the $E\times B$
are known as soon as the perpendicular particle fluxes are modelled. On the other hand, (3.22) illustrates that the $E\times B$![]() turbulent particle flux does contribute to the polarisation current and thus to the charge balance equation for the mean-field potential $\bar {\phi }$
turbulent particle flux does contribute to the polarisation current and thus to the charge balance equation for the mean-field potential $\bar {\phi }$![]() .
.
Many more closure terms are present apart from the aforementioned convective fluxes. The terms on the right-hand side of (3.8)–(3.12), depending on multiple plasma state quantities, will obviously give rise to a part which can be determined based on mean-field quantities and a part which cannot, e.g. $\overline {V_{\|} \nabla_{\|} p} = \tilde {V}_{\|}\nabla_{\|} \bar {p}+\overline {V_{\|}'' \nabla_{\|} p}$![]() . Lastly, any nonlinear dependence on the plasma state in the classical transport expressions ($\boldsymbol{\varPi}$
. Lastly, any nonlinear dependence on the plasma state in the classical transport expressions ($\boldsymbol{\varPi}$![]() , $R_{ei,\|}$
, $R_{ei,\|}$![]() , $\it{q}_{\|}$
, $\it{q}_{\|}$![]() , $Q_{\mathrm {ei}}$
, $Q_{\mathrm {ei}}$![]() ) or source terms ($S_{n}$
) or source terms ($S_{n}$![]() , $\boldsymbol {S}_{m}$
, $\boldsymbol {S}_{m}$![]() , $S_{p}$
, $S_{p}$![]() ) will likewise give rise to closure terms. The collisional plasma viscous stress, parallel friction force and parallel heat fluxes typically scale with $\sim T_e^{3/2}$
) will likewise give rise to closure terms. The collisional plasma viscous stress, parallel friction force and parallel heat fluxes typically scale with $\sim T_e^{3/2}$![]() and a plasma state gradient, possibly leading to strong nonlinearities. The interaction between the turbulence and neutral particles likewise introduces nonlinearities in the particle, momentum and energy sources terms. These closure terms are always neglected in mean-field transport codes as far as the authors are aware. Future work will have to determine if these hypotheses are warranted.
and a plasma state gradient, possibly leading to strong nonlinearities. The interaction between the turbulence and neutral particles likewise introduces nonlinearities in the particle, momentum and energy sources terms. These closure terms are always neglected in mean-field transport codes as far as the authors are aware. Future work will have to determine if these hypotheses are warranted.
The mean-field equations derived in this section bridge the theoretical gap between the turbulent equations presented in the previous section, which describe the instantaneous dynamics of the turbulence and the equations solved in mean-field transport codes which describe the transport on longer time and length scales. The mean-field equations derived here correspond analytically to the instantaneous equations of the previous chapter through the rigorous averaging methodology that is followed. Comparing these equations with the equations solved in mean-field transport codes gives a clear interpretation and mathematical definition of the terms being modelled in these codes and which terms are being neglected. Moreover, it clearly defines the exact averages that are being used and thus allows us to give a precise meaning to the quantities which are being solved for in mean-field transport codes. It shows for example that the density which is solved for is indeed the Reynolds or ensemble average density, while temperatures and parallel velocity are to be interpreted as Favre or density weighed quantities.
Evaluating the closure terms using data from turbulence codes (providing data on the instantaneous fluctuations) will allow to establish which closure terms are important and should be added to mean-field codes, and which ones can be neglected. A further analysis of these closure terms and turbulence code data will then allow to develop simplified models which can be used to model these terms more reliably in mean-field codes. This article will mostly consider the turbulent $E\times B$![]() particle and heat transport, which are considered to be of crucial importance, and which are indeed known to be large compared with the mean-field fluxes (Scott Reference Scott2003; Wesson Reference Wesson2004; Fundamenski Reference Fundamenski2010). Moreover, the information gained from modelling this relatively simple term could be used to further develop the applied methodology to assess the important terms and to elaborate models for the dominant closure terms.
particle and heat transport, which are considered to be of crucial importance, and which are indeed known to be large compared with the mean-field fluxes (Scott Reference Scott2003; Wesson Reference Wesson2004; Fundamenski Reference Fundamenski2010). Moreover, the information gained from modelling this relatively simple term could be used to further develop the applied methodology to assess the important terms and to elaborate models for the dominant closure terms.
As $\boldsymbol {\varGamma }_{n,t,E}$![]() , $\boldsymbol {\varGamma }_{p_{{i}},t,E}$
, $\boldsymbol {\varGamma }_{p_{{i}},t,E}$![]() and $\boldsymbol {\varGamma }_{p_{{e}},t,E}$
and $\boldsymbol {\varGamma }_{p_{{e}},t,E}$![]() have been shown to be governed by the correlations between density, temperature and potential fluctuations, we aim to find a measure for the intensity of these fluctuations, and relate it to the resulting fluxes. The $E\times B$
have been shown to be governed by the correlations between density, temperature and potential fluctuations, we aim to find a measure for the intensity of these fluctuations, and relate it to the resulting fluxes. The $E\times B$![]() turbulent kinetic energy ($k_{E}$
turbulent kinetic energy ($k_{E}$![]() , see (5.1a–c) for definition) provides a direct measure of the characteristic $E\times B$
, see (5.1a–c) for definition) provides a direct measure of the characteristic $E\times B$![]() drift velocity of particles in the fluctuating electrostatic field. The eddies and convection cells formed by fluctuations in the electrostatic field are exactly the motions that cause the anomalous transport observed in the SOL that is of interest here (Scott Reference Scott2003; Balescu et al. Reference Balescu, Vlad, Spineanu and Misguich2004; Wesson Reference Wesson2004; Fundamenski Reference Fundamenski2010). Hence, a link between $k_{E}$
drift velocity of particles in the fluctuating electrostatic field. The eddies and convection cells formed by fluctuations in the electrostatic field are exactly the motions that cause the anomalous transport observed in the SOL that is of interest here (Scott Reference Scott2003; Balescu et al. Reference Balescu, Vlad, Spineanu and Misguich2004; Wesson Reference Wesson2004; Fundamenski Reference Fundamenski2010). Hence, a link between $k_{E}$![]() and the effective turbulent diffusion coefficient is expected and has indeed been observed in earlier work (Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2020, Reference Coosemans, Dekeyser and Baelmans2021b; Coosemans, Dekeyser & Baelmans Reference Coosemans, Dekeyser and Baelmans2021a; Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2022).
and the effective turbulent diffusion coefficient is expected and has indeed been observed in earlier work (Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2020, Reference Coosemans, Dekeyser and Baelmans2021b; Coosemans, Dekeyser & Baelmans Reference Coosemans, Dekeyser and Baelmans2021a; Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2022).
To further refine scalings for the turbulent fluxes, the turbulent enstrophy ($\zeta _{E}$![]() , see (A10a–c) for definition) can also be considered. It also provides a measure for the intensity of the turbulence and is also conserved in 2-D inviscid hydrodynamic turbulence. However, the cascade dynamics (inverse cascade for the kinetic energy, direct cascade for enstrophy) and through that the length scales which mostly contribute to both quantities (enstrophy concentrated on shorter length scales) differ (Camargo, Biskamp & Scott Reference Camargo, Biskamp and Scott1995; Yakhot Reference Yakhot2004; Alexakis & Doering Reference Alexakis and Doering2006; Fundamenski Reference Fundamenski2010; Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2020). Hence, they are expected to provide complementary information. In practical terms, the enstrophy allows us to complete the scaling for the transport coefficients with a turbulent time scale. It could be argued that, while $\sqrt {k_{E}/m}$
, see (A10a–c) for definition) can also be considered. It also provides a measure for the intensity of the turbulence and is also conserved in 2-D inviscid hydrodynamic turbulence. However, the cascade dynamics (inverse cascade for the kinetic energy, direct cascade for enstrophy) and through that the length scales which mostly contribute to both quantities (enstrophy concentrated on shorter length scales) differ (Camargo, Biskamp & Scott Reference Camargo, Biskamp and Scott1995; Yakhot Reference Yakhot2004; Alexakis & Doering Reference Alexakis and Doering2006; Fundamenski Reference Fundamenski2010; Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2020). Hence, they are expected to provide complementary information. In practical terms, the enstrophy allows us to complete the scaling for the transport coefficients with a turbulent time scale. It could be argued that, while $\sqrt {k_{E}/m}$![]() defines a velocity scale for the particles in the $E\times B$
defines a velocity scale for the particles in the $E\times B$![]() eddies, $\sqrt {m/\zeta _{E}}$
eddies, $\sqrt {m/\zeta _{E}}$![]() adds a time scale. Coosemans et al. (Reference Coosemans, Dekeyser and Baelmans2020) showed that including the enstrophy does indeed allow a more accurate prediction of the turbulent fluxes.
adds a time scale. Coosemans et al. (Reference Coosemans, Dekeyser and Baelmans2020) showed that including the enstrophy does indeed allow a more accurate prediction of the turbulent fluxes.
4. Mean-field energy theorem
This section and the next will derive equations for the kinetic energy and enstrophy in the turbulent fluctuations, which can serve as a theoretical basis for modelling the turbulent kinetic energy and enstrophy and through that the turbulent fluxes. Moreover, equations will be derived for other energy forms in the plasma as well, yielding an energy theorem. This in turn provides an interesting viewpoint into the turbulence dynamics in the plasma edge.
4.1. Perpendicular kinetic energy equations
This section will focus on the kinetic energy in the perpendicular velocity fluctuations and its relation to the other energy forms in the plasma. We define the perpendicular total ($E_{{k},\perp }$![]() ), mean-flow ($E_{k,m,\perp }$
), mean-flow ($E_{k,m,\perp }$![]() ) and turbulent ($k_{\perp }$
) and turbulent ($k_{\perp }$![]() ) kinetic energies as
) kinetic energies as
where $\boldsymbol {V}_{0,\perp }$![]() contains the perpendicular velocity components that are relevant for the ion inertia. As discussed in the previous section, we assume that $\boldsymbol {V}_{0,\perp }=\boldsymbol {V}_{E}+\boldsymbol {V}_{*,i}$
contains the perpendicular velocity components that are relevant for the ion inertia. As discussed in the previous section, we assume that $\boldsymbol {V}_{0,\perp }=\boldsymbol {V}_{E}+\boldsymbol {V}_{*,i}$![]() . Note that $E_{{k},\perp }$
. Note that $E_{{k},\perp }$![]() varies rapidly in time and space as it follows the instantaneous fluctuations, while $E_{k,m,\perp }$
varies rapidly in time and space as it follows the instantaneous fluctuations, while $E_{k,m,\perp }$![]() and $k_{\perp }$
and $k_{\perp }$![]() are ensemble-averaged quantities that do not change at these small scales. The latter two are constant in time in a statistical steady state, while the former is not. Note also that the sum of mean flow and turbulent kinetic energy per unit volume equals the averaged total kinetic energy per unit volume
are ensemble-averaged quantities that do not change at these small scales. The latter two are constant in time in a statistical steady state, while the former is not. Note also that the sum of mean flow and turbulent kinetic energy per unit volume equals the averaged total kinetic energy per unit volume
The derivation of the turbulent kinetic energy equation presented here is based on the procedure applied by Scott (Reference Scott2003). Garcia et al. (Reference Garcia, Naulin, Nielsen and Rasmussen2006) and Tran et al. (Reference Tran, Kim, Jhang and Kim2019) likewise followed a similar scheme. These derivations are refined here by taking the density fluctuations into account in the averaging operators and by considering a number of terms which were neglected in these references. To limit the number of closure terms, we make use of the Favre averages introduced in § 3. Note that an analogous procedure has also been applied to a reduced turbulence description for a 2-D, electrostatic, sheath-limited, $E\times B$![]() -only SOL in earlier work (Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2021b).
-only SOL in earlier work (Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2021b).
The total perpendicular kinetic energy equation is obtained by multiplying the charge balance equation (2.20) with the electrostatic potential
and rewriting the different terms. The polarisation current on the left-hand side introduces the kinetic energy in the equation. This term is first rewritten as
In this expression, the second term on the right-hand side is in turn rewritten as

In this derivation, we made use of continuity equation (2.1) and the definition of the polarisation current (2.9) (supplemented with (2.11)), with the convection velocity given by $\boldsymbol {V}_{C}$![]() in both equations. Furthermore, common vector calculus identities were used.
in both equations. Furthermore, common vector calculus identities were used.
The first term on the right-hand side of (4.3) is straightforwardly rewritten as $\phi \boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {J}_{\|}=\boldsymbol {\nabla }\boldsymbol {\cdot }\phi \boldsymbol {J}_{\|}-J_{\|}\boldsymbol {\nabla }_{\|}\phi$![]() . Following Scott (Reference Scott2003), the second term is then rewritten as
. Following Scott (Reference Scott2003), the second term is then rewritten as
Filling out expressions (4.4)–(4.6) in (4.3), the total perpendicular kinetic energy equation is found

To arrive at equations for $E_{k,m,\perp }$![]() and $k_{\perp }$
and $k_{\perp }$![]() defined in (4.1a–c), the $E_{{k},\perp }$
defined in (4.1a–c), the $E_{{k},\perp }$![]() equation (4.7) should be averaged and split in a contribution due to mean flows and a contribution due to fluctuations. The procedure to obtain an equation for $E_{k,m,\perp }$
equation (4.7) should be averaged and split in a contribution due to mean flows and a contribution due to fluctuations. The procedure to obtain an equation for $E_{k,m,\perp }$![]() is rather similar to that used for $E_{{k},\perp }$
is rather similar to that used for $E_{{k},\perp }$![]() . For this, we start from the averaged charge balance equation multiplied with the average electrostatic potential
. For this, we start from the averaged charge balance equation multiplied with the average electrostatic potential
The terms on the right-hand side will be manipulated in exact analogy to those in the total kinetic energy equation. Some slight complications arise for the polarisation current term, however, because we need the dot product between $\bar {\boldsymbol {J}}_{p}$![]() and the Favre-averaged potential gradient to form the time rate of change of the mean-field perpendicular kinetic energy $E_{k,m,\perp }$
and the Favre-averaged potential gradient to form the time rate of change of the mean-field perpendicular kinetic energy $E_{k,m,\perp }$![]()
The last term on the right-hand side, which we will call ‘Favre averaging term’, arises because Favre averages and gradients do not commute. This then leads to the following equation:

Taking the difference between the time average of (4.7) and (4.10), an equation for the perpendicular turbulent kinetic energy is finally obtained

The manipulations performed in this section and the equations in which they resulted have largely been based on the seminal paper by Scott (Reference Scott2003). However, a clearer definition of the averaging operators has been used here, which consistently includes density fluctuations. Next to changes in the exact form of some terms in terms of averages and fluctuations, this leads to the appearance of the ‘Favre term’ in (4.10) and (4.11) (seventh term on the right-hand side). Furthermore, particle and momentum sources ($S_{n}$![]() and $\boldsymbol {S}_{m}$
and $\boldsymbol {S}_{m}$![]() ) have been retained in the equation set (including their possible fluctuations) as well as the ${\textrm {D}\boldsymbol {b}}/{\textrm {D} t}$
) have been retained in the equation set (including their possible fluctuations) as well as the ${\textrm {D}\boldsymbol {b}}/{\textrm {D} t}$![]() term which were not included in the paper by Scott (Reference Scott2003). Also, we chose to keep the general form of the viscous stress tensor $\boldsymbol{\varPi}$
term which were not included in the paper by Scott (Reference Scott2003). Also, we chose to keep the general form of the viscous stress tensor $\boldsymbol{\varPi}$![]() instead of assuming a particular model for it. On the other hand, magnetic field fluctuations have been neglected here, while they were (partly) maintained in the original paper.
instead of assuming a particular model for it. On the other hand, magnetic field fluctuations have been neglected here, while they were (partly) maintained in the original paper.
We leave a discussion of the perpendicular kinetic energy equations (4.7), (4.10) and (4.11) and the physics they included for § 4.4.
4.2. Parallel kinetic energy equations
There is also kinetic energy in the parallel ion plasma velocity, both in the mean-field and the fluctuating component. In analogy with the perpendicular kinetic energies, we write the parallel kinetic energies as
Transport equations for the parallel kinetic energy can be obtained in a rather straightforward way which is very similar to the typical procedure used in hydrodynamic turbulence. An equation for $E_{{k},\|}$![]() can be obtained by multiplying the parallel momentum equation (2.23) with $V_{\|}$
can be obtained by multiplying the parallel momentum equation (2.23) with $V_{\|}$![]()

In this derivation, the ion continuity equation (2.1) has been used, in which the convection velocity is assumed to be $\boldsymbol {V}_{C}$![]() , as in the ion momentum equation. Likewise, a mean-field parallel kinetic energy equation is constructed by multiplying the average of (2.23) with $\tilde {V}_{\|}$
, as in the ion momentum equation. Likewise, a mean-field parallel kinetic energy equation is constructed by multiplying the average of (2.23) with $\tilde {V}_{\|}$![]() . This yields
. This yields

Taking the difference between the average of (4.13) and (4.14), an equation for the parallel turbulent kinetic energy is found as

Beside the $\textrm {D}\boldsymbol {b}/\textrm {D} t$![]() terms, the interpretation of these equations is rather standard and deviates little from that for the kinetic energy in hydrodynamic turbulence. We will come back to this interpretation in § 4.4.
terms, the interpretation of these equations is rather standard and deviates little from that for the kinetic energy in hydrodynamic turbulence. We will come back to this interpretation in § 4.4.
4.3. Magnetic energy equations
As mentioned above, the magnetic field can be described in terms of the magnetic vector potential
The magnetic energy can then be decomposed as
where the last term enters through reworking the scalar product between $\boldsymbol {\nabla } \times \boldsymbol {A}_{\|}$![]() and $\boldsymbol {\nabla } \times \boldsymbol {A}_{\perp }$
and $\boldsymbol {\nabla } \times \boldsymbol {A}_{\perp }$![]() . In this work, we will only study the first term. The dynamics of the second contribution is not included in the equation set considered here, i.e. $\boldsymbol {A}_{\perp }$
. In this work, we will only study the first term. The dynamics of the second contribution is not included in the equation set considered here, i.e. $\boldsymbol {A}_{\perp }$![]() is in equilibrium at the time scales of interest. The third term could be assumed to be small on the hypothesis that the parallel gradient of the equilibrium quantity $\boldsymbol {A}_{\perp }$
is in equilibrium at the time scales of interest. The third term could be assumed to be small on the hypothesis that the parallel gradient of the equilibrium quantity $\boldsymbol {A}_{\perp }$![]() is small.
is small.
Hence, we define the (relevant part of the) total, mean-field and turbulent magnetic energies as

Note that a regular Reynolds decomposition is used in these definitions since the magnetic energy per unit volume is independent of the density. Remark also that the sum of mean-field and turbulent magnetic energy equals the averaged total magnetic energy
Following Scott (Reference Scott2003), an equation for the total magnetic energy is derived by taking the product of the parallel current with Ohm's law (2.21) divided by $en$![]()
The left-hand side can be rewritten using (2.22) to find
For the first term in the above equation, it is easy to show that
So finally, we get the total magnetic energy equation
Following an exactly analogous derivation using the average parallel current $\bar {J}_{\|}$![]() and the average Ohm's law (3.10), the mean-field magnetic energy is found as
and the average Ohm's law (3.10), the mean-field magnetic energy is found as
We remark here that $\bar {J}_{\|}\partial \bar {A}_{\|}/\partial t$![]() is in general non-zero during stationary tokamak operation. This is in fact the power inserted into the plasma due to the electromagnetic induction of the main transformer. This term is decomposed in $\partial E _{B,m}/\partial t$
is in general non-zero during stationary tokamak operation. This is in fact the power inserted into the plasma due to the electromagnetic induction of the main transformer. This term is decomposed in $\partial E _{B,m}/\partial t$![]() , which would ideally be zero in a stationary state (constant average magnetic field) and the transport term $-\boldsymbol {\nabla }\boldsymbol {\cdot }(\boldsymbol {\nabla }_{\perp }\bar {A}_{\|}/\mu \partial \bar {A}_{\|}/\partial t)$
, which would ideally be zero in a stationary state (constant average magnetic field) and the transport term $-\boldsymbol {\nabla }\boldsymbol {\cdot }(\boldsymbol {\nabla }_{\perp }\bar {A}_{\|}/\mu \partial \bar {A}_{\|}/\partial t)$![]() . In § 3, it has already been discussed that $\partial \bar {A}_{\|}/\partial t$
. In § 3, it has already been discussed that $\partial \bar {A}_{\|}/\partial t$![]() is non-zero in stationary operation. Secondly, $-\boldsymbol {\nabla }_{\perp }\bar {A}_{\|}/\mu$
is non-zero in stationary operation. Secondly, $-\boldsymbol {\nabla }_{\perp }\bar {A}_{\|}/\mu$![]() is related to the total plasma current enclosed by the flux surface on which it is evaluated and should thus be non-zero as well. Hence, $-\boldsymbol {\nabla }_{\perp }\bar {A}_{\|}/\mu \partial \bar {A}_{\|}/\partial t$
is related to the total plasma current enclosed by the flux surface on which it is evaluated and should thus be non-zero as well. Hence, $-\boldsymbol {\nabla }_{\perp }\bar {A}_{\|}/\mu \partial \bar {A}_{\|}/\partial t$![]() can be interpreted as an influx of magnetic energy from the boundary of the computational domain, as induced by the central solenoid.
can be interpreted as an influx of magnetic energy from the boundary of the computational domain, as induced by the central solenoid.
Taking the difference between the average of (4.23) and (4.24), an equation for the energy in the magnetic field fluctuations is obtained

4.4. Energy theorem
This section illustrates the energetic couplings between the perpendicular kinetic energy (mean-field (4.10) and turbulent (4.11)), thermal energy (electron (3.9) and ions (3.8)), parallel kinetic energy (mean-field (4.14) and turbulent (4.15)) and magnetic energy (mean-field (4.24) and turbulent (4.25)) and thus of the different pathways for the energy to get into and out of the turbulence. This discussion is largely based on the insight provided by Scott (Reference Scott2003).
Our main interest is the perpendicular turbulent kinetic energy which is supposedly driving the turbulent transport of heat and particles. As such, we first consider the left-hand side of (4.11). The first term is the time rate of change of the turbulent kinetic energy. Then, all terms under the divergence operator represent fluxes transporting turbulent kinetic energy from one location to another. The first flux is the convection of $k_{\perp }$![]() by the mean-field velocity, the second one the convection by turbulent fluctuations and the third one a flux due to viscous stresses. These terms also appear in regular hydrodynamic turbulence, see for example Pope (Reference Pope2015) and Canuto (Reference Canuto1997). Next, a flux due to electrostatic potential and current fluctuations follows and then a flux of pressure due to $E\times B$
by the mean-field velocity, the second one the convection by turbulent fluctuations and the third one a flux due to viscous stresses. These terms also appear in regular hydrodynamic turbulence, see for example Pope (Reference Pope2015) and Canuto (Reference Canuto1997). Next, a flux due to electrostatic potential and current fluctuations follows and then a flux of pressure due to $E\times B$![]() velocity fluctuations. Scott (Reference Scott2003) argues that that $\boldsymbol {\nabla }\boldsymbol {\cdot }(\overline {\phi '\boldsymbol {J}'}+\overline {p'\boldsymbol {V}_{E}'})\approx \boldsymbol {\nabla }\boldsymbol {\cdot }\overline {\phi '\boldsymbol {J}_{\|}'}$
velocity fluctuations. Scott (Reference Scott2003) argues that that $\boldsymbol {\nabla }\boldsymbol {\cdot }(\overline {\phi '\boldsymbol {J}'}+\overline {p'\boldsymbol {V}_{E}'})\approx \boldsymbol {\nabla }\boldsymbol {\cdot }\overline {\phi '\boldsymbol {J}_{\|}'}$![]() , since $p\boldsymbol {V}_{E}$
, since $p\boldsymbol {V}_{E}$![]() cancels with $\phi \boldsymbol {J}_{\perp }$
cancels with $\phi \boldsymbol {J}_{\perp }$![]() due to Pointing cancellation. Furthermore, it can be shown that $-\boldsymbol {\nabla }\boldsymbol {\cdot }(\phi \boldsymbol {J}_{*} + p\boldsymbol {V}_{E}) = \boldsymbol {\nabla }\boldsymbol {\cdot }( \boldsymbol {\nabla }(\bar {p\phi })\times \boldsymbol {b}/B )$
due to Pointing cancellation. Furthermore, it can be shown that $-\boldsymbol {\nabla }\boldsymbol {\cdot }(\phi \boldsymbol {J}_{*} + p\boldsymbol {V}_{E}) = \boldsymbol {\nabla }\boldsymbol {\cdot }( \boldsymbol {\nabla }(\bar {p\phi })\times \boldsymbol {b}/B )$![]() , which vanishes in 1-D radial geometries (Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2021b). The remaining transport due to $\overline {\phi '\boldsymbol {J}_{\|}'}$
, which vanishes in 1-D radial geometries (Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2021b). The remaining transport due to $\overline {\phi '\boldsymbol {J}_{\|}'}$![]() thus constitutes a non-convective parallel transport term that does not have an equivalent in hydrodynamic turbulence. Note that all these transport terms, except for mean-field convection, constitute closure terms, and that little quantitative information is available for them a priori. Singh & Diamond (Reference Singh and Diamond2020) focus on the radial transport of turbulence intensity and investigate when the associated terms are important. As far as the authors are aware, the $\overline {\phi '\boldsymbol {J}_{\|}'}$
thus constitutes a non-convective parallel transport term that does not have an equivalent in hydrodynamic turbulence. Note that all these transport terms, except for mean-field convection, constitute closure terms, and that little quantitative information is available for them a priori. Singh & Diamond (Reference Singh and Diamond2020) focus on the radial transport of turbulence intensity and investigate when the associated terms are important. As far as the authors are aware, the $\overline {\phi '\boldsymbol {J}_{\|}'}$![]() flux has received very little attention in the literature. However, § 6 will argue it may play an important role in plasma edge turbulence.
flux has received very little attention in the literature. However, § 6 will argue it may play an important role in plasma edge turbulence.
Next, the coupling between mean-field and turbulent kinetic energy is considered. As in hydrodynamic turbulence, the Reynolds stress (RS) term (third term on the right-hand side of (4.10) and (4.11), different sign in both) exchanges energy between the turbulent and mean-field kinetic energy. While in 3-D hydrodynamic turbulence this term typically drives the turbulence, in plasma edge physics it is expected to act like a sink of $k_{\perp }$![]() and thus a source of $E_{k,m,\perp }$
and thus a source of $E_{k,m,\perp }$![]() because of the inverse energy cascade. Hence, this term is expected to be important close to the separatrix, where strong shear flows tend to develop, which are partly fed by the turbulent kinetic energy by tearing apart small eddies. Moreover, this term is also expected to play an important role in the generation of these shear flows (Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005; Manz et al. Reference Manz, Xu, Fedorczak, Thakur and Tynan2012; Held et al. Reference Held, Wiesenberger, Kube and Kendl2018). However, when the turbulence is sufficiently damped and when the flow shear is sufficiently strong, the RS term may act like a source of $k_{\perp }$
because of the inverse energy cascade. Hence, this term is expected to be important close to the separatrix, where strong shear flows tend to develop, which are partly fed by the turbulent kinetic energy by tearing apart small eddies. Moreover, this term is also expected to play an important role in the generation of these shear flows (Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005; Manz et al. Reference Manz, Xu, Fedorczak, Thakur and Tynan2012; Held et al. Reference Held, Wiesenberger, Kube and Kendl2018). However, when the turbulence is sufficiently damped and when the flow shear is sufficiently strong, the RS term may act like a source of $k_{\perp }$![]() through the Kelvin–Helmholtz (KH) instability (Rogers & Dorland Reference Rogers and Dorland2005; Myra et al. Reference Myra, D'Ippolito, Russell, Umansky and Baver2016; Giacomin & Ricci Reference Giacomin and Ricci2020). In addition, the ‘Favre term’, seventh term on the right-hand side in both equations, also exchanges energy between mean-field and turbulent kinetic energy. This term appeared due to the non-commutativity of the gradient and Favre averaging operators. Thus, this term only appeared in the equation because of the rigorous average techniques that have been applied and had not been identified in the literature before as far as the authors are aware. The RSs clearly constitutes a closure term. The Favre term contains closure terms in $\bar {\boldsymbol {J}}_{p}$
through the Kelvin–Helmholtz (KH) instability (Rogers & Dorland Reference Rogers and Dorland2005; Myra et al. Reference Myra, D'Ippolito, Russell, Umansky and Baver2016; Giacomin & Ricci Reference Giacomin and Ricci2020). In addition, the ‘Favre term’, seventh term on the right-hand side in both equations, also exchanges energy between mean-field and turbulent kinetic energy. This term appeared due to the non-commutativity of the gradient and Favre averaging operators. Thus, this term only appeared in the equation because of the rigorous average techniques that have been applied and had not been identified in the literature before as far as the authors are aware. The RSs clearly constitutes a closure term. The Favre term contains closure terms in $\bar {\boldsymbol {J}}_{p}$![]() , while the $\overline {n'\boldsymbol {\nabla }\phi '}$
, while the $\overline {n'\boldsymbol {\nabla }\phi '}$![]() factor can be calculated from $\boldsymbol {\varGamma }_{n,t,E}$
factor can be calculated from $\boldsymbol {\varGamma }_{n,t,E}$![]() .
.
Comparing the right-hand side of the thermal energy equations (3.8) and (3.9) with that of the kinetic energy equations (4.10) and (4.11), it can be seen that interchange terms involving $p\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {V}_{E}$![]() appear in all of them. Hence, the fluctuations of this interchange term exchange energy between the turbulence and the thermal energy. This energy transfer could occur in both directions (from thermal energy to turbulence and vice versa), see § 6. However, it is expected that this interchange term will provide an important source of the turbulence on the outboard side of the tokamak, especially in the SOL (Scott Reference Scott2003, Reference Scott2005; Ribeiro & Scott Reference Ribeiro and Scott2005). While the interchange term is a closure term, an analytical model for it has been found; see these same references and § 6. The viscous stress and $\nabla_{\perp}p _{{i}}\boldsymbol {\cdot }\boldsymbol {V}_{p}$
appear in all of them. Hence, the fluctuations of this interchange term exchange energy between the turbulence and the thermal energy. This energy transfer could occur in both directions (from thermal energy to turbulence and vice versa), see § 6. However, it is expected that this interchange term will provide an important source of the turbulence on the outboard side of the tokamak, especially in the SOL (Scott Reference Scott2003, Reference Scott2005; Ribeiro & Scott Reference Ribeiro and Scott2005). While the interchange term is a closure term, an analytical model for it has been found; see these same references and § 6. The viscous stress and $\nabla_{\perp}p _{{i}}\boldsymbol {\cdot }\boldsymbol {V}_{p}$![]() terms likewise exchange energy between the kinetic energy (both mean-field and turbulent) and ion thermal energy. The former acts like a sink dissipating kinetic energy into thermal energy. Coosemans et al. (Reference Coosemans, Dekeyser and Baelmans2021b, Reference Coosemans, Dekeyser and Baelmans2022) found it to be of secondary importance for the $k_{\perp }$
terms likewise exchange energy between the kinetic energy (both mean-field and turbulent) and ion thermal energy. The former acts like a sink dissipating kinetic energy into thermal energy. Coosemans et al. (Reference Coosemans, Dekeyser and Baelmans2021b, Reference Coosemans, Dekeyser and Baelmans2022) found it to be of secondary importance for the $k_{\perp }$![]() balance for simulations with the TOKAM2D turbulence code (Sarazin & Ghendrih Reference Sarazin and Ghendrih1998; Moulton et al. Reference Moulton, Marandet, Tamain, Ghendrih and Futtersack2014; Baudoin et al. Reference Baudoin, Tamain, Ciraolo, Futtersack, Gallo, Ghendrih, Marandet, Nace and Norscini2016; Marandet et al. Reference Marandet, Nace, Valentinuzzi, Tamain, Bufferand, Ciraolo, Genesio and Mellet2016; Nace Reference Nace2018). Further research is required to quantify the importance of the latter term. Again, both terms appear as closure terms in the $k_{\perp }$
balance for simulations with the TOKAM2D turbulence code (Sarazin & Ghendrih Reference Sarazin and Ghendrih1998; Moulton et al. Reference Moulton, Marandet, Tamain, Ghendrih and Futtersack2014; Baudoin et al. Reference Baudoin, Tamain, Ciraolo, Futtersack, Gallo, Ghendrih, Marandet, Nace and Norscini2016; Marandet et al. Reference Marandet, Nace, Valentinuzzi, Tamain, Bufferand, Ciraolo, Genesio and Mellet2016; Nace Reference Nace2018). Further research is required to quantify the importance of the latter term. Again, both terms appear as closure terms in the $k_{\perp }$![]() equation.
equation.
Then, the terms involving $J_{\|}\nabla_{\|}\phi$![]() in the $E_{k,m,\perp }$
in the $E_{k,m,\perp }$![]() and $k_{\perp }$
and $k_{\perp }$![]() equation can be shown to exchange energy with the mean-field and turbulent magnetic energy ((4.24) and (4.25) respectively). Furthermore, the other two terms on the right-hand side of (4.24) and (4.25) exchange energy between this magnetic energy and the electron thermal energy in (3.9). The last term in the magnetic energy equations is due to electron–ion friction and is expected to dissipate magnetic energy, providing a unidirectional transfer to the thermal energy. The first term on the right-hand side of the equation is assumed to allow energy transfer from thermal energy to magnetic energy and from there to the turbulent kinetic energy. Hence, this constitutes a second channel by which energy can be injected from the thermal energy into the turbulence (next to the interchange channel) (Scott Reference Scott2003, Reference Scott2005). This transfer channel is related to the dynamics parallel to the magnetic field and especially the drift-wave (DW) instability is expected to act on this channel. Because the parallel dynamics has more freedom to evolve in the closed field line region than in the SOL, it is expected to be especially important there (Scott Reference Scott2003, Reference Scott2005; Ribeiro & Scott Reference Ribeiro and Scott2005).
equation can be shown to exchange energy with the mean-field and turbulent magnetic energy ((4.24) and (4.25) respectively). Furthermore, the other two terms on the right-hand side of (4.24) and (4.25) exchange energy between this magnetic energy and the electron thermal energy in (3.9). The last term in the magnetic energy equations is due to electron–ion friction and is expected to dissipate magnetic energy, providing a unidirectional transfer to the thermal energy. The first term on the right-hand side of the equation is assumed to allow energy transfer from thermal energy to magnetic energy and from there to the turbulent kinetic energy. Hence, this constitutes a second channel by which energy can be injected from the thermal energy into the turbulence (next to the interchange channel) (Scott Reference Scott2003, Reference Scott2005). This transfer channel is related to the dynamics parallel to the magnetic field and especially the drift-wave (DW) instability is expected to act on this channel. Because the parallel dynamics has more freedom to evolve in the closed field line region than in the SOL, it is expected to be especially important there (Scott Reference Scott2003, Reference Scott2005; Ribeiro & Scott Reference Ribeiro and Scott2005).
Note that, in the electrostatic case in which $A_{\|}'=0$![]() , the left-hand side of (4.25) vanishes. Nonetheless, the DW coupling remains active, be it in a slightly simplified form. The terms $-\overline {J_{\|}'(\nabla_{\|}p_{{e}}/(ne))'}+\overline {J_{\|}'(R_{ei,\|}/(n e))'}$
, the left-hand side of (4.25) vanishes. Nonetheless, the DW coupling remains active, be it in a slightly simplified form. The terms $-\overline {J_{\|}'(\nabla_{\|}p_{{e}}/(ne))'}+\overline {J_{\|}'(R_{ei,\|}/(n e))'}$![]() in the electron thermal energy equation (3.9) could then be replaced by $-\overline {J_{\|}'\nabla_{\|}\phi '}$
in the electron thermal energy equation (3.9) could then be replaced by $-\overline {J_{\|}'\nabla_{\|}\phi '}$![]() , such that the coupling is directly between the thermal energy and the turbulent kinetic energy (without the mediation of the magnetic energy). Furthermore we remark that the left-hand side of the mean-field magnetic energy equation (4.24) actually represents the power induced in the plasma through electromagnetic induction by the central solenoid. As this power is injected into the magnetic energy, it could in theory not just be dissipated through the resistive term, but may also find its way to the mean-field kinetic energy through the $\bar {J}_{\|}\nabla_{\|}\bar {\phi }$
, such that the coupling is directly between the thermal energy and the turbulent kinetic energy (without the mediation of the magnetic energy). Furthermore we remark that the left-hand side of the mean-field magnetic energy equation (4.24) actually represents the power induced in the plasma through electromagnetic induction by the central solenoid. As this power is injected into the magnetic energy, it could in theory not just be dissipated through the resistive term, but may also find its way to the mean-field kinetic energy through the $\bar {J}_{\|}\nabla_{\|}\bar {\phi }$![]() term.
term.
Next, the $\textrm {D}\boldsymbol {b}/\textrm {D} t$![]() terms in the perpendicular kinetic energy equations (4.10) and (4.11) exchange energy with the parallel kinetic energies in (4.14) and (4.15). These terms are due to changes in the magnetic field direction. Notice that the $\textrm {D}\boldsymbol {b}/\textrm {D} t$
terms in the perpendicular kinetic energy equations (4.10) and (4.11) exchange energy with the parallel kinetic energies in (4.14) and (4.15). These terms are due to changes in the magnetic field direction. Notice that the $\textrm {D}\boldsymbol {b}/\textrm {D} t$![]() term in the $k_{\perp }$
term in the $k_{\perp }$![]() equation not only exchanges energy with $k_{\|}$
equation not only exchanges energy with $k_{\|}$![]() , but also with $E_{{k},m,\|}$
, but also with $E_{{k},m,\|}$![]() . Likewise, this term allows energy transfer from $E_{k,m,\perp }$
. Likewise, this term allows energy transfer from $E_{k,m,\perp }$![]() to $E_{{k},m,\|}$
to $E_{{k},m,\|}$![]() and $k_{\|}$
and $k_{\|}$![]() . Note that these terms only appear in the perpendicular kinetic energy equations because the $\boldsymbol {J}_{p,\|}$
. Note that these terms only appear in the perpendicular kinetic energy equations because the $\boldsymbol {J}_{p,\|}$![]() contribution to the polarisation current (defined in (2.14)) has been retained (which is why they were not included in Scott Reference Scott2003). The $\textrm {D}\boldsymbol {b}/\textrm {D} t$
contribution to the polarisation current (defined in (2.14)) has been retained (which is why they were not included in Scott Reference Scott2003). The $\textrm {D}\boldsymbol {b}/\textrm {D} t$![]() contributions to the $\boldsymbol {J}_{p,E}$
contributions to the $\boldsymbol {J}_{p,E}$![]() and $\boldsymbol {J}_{p,*}$
and $\boldsymbol {J}_{p,*}$![]() (see definitions (2.15) and (2.16)) to the contrary do not individually lead to additional terms in any of the energy equations. The importance of these energy transfer channels is unknown. It may be expected that their magnitude and sign depend on the direction of the magnetic field in the reactor (forward field or reverse field). Note that these terms represent the only direct coupling between parallel and perpendicular kinetic energies. However, energy could also be transferred between them by the mediation of the ion and electron thermal energy. Furthermore, it is very possible that the parallel kinetic energy dynamics implicitly impacts the turbulence, for example by its impact on or competition with other energy transfer channels.
(see definitions (2.15) and (2.16)) to the contrary do not individually lead to additional terms in any of the energy equations. The importance of these energy transfer channels is unknown. It may be expected that their magnitude and sign depend on the direction of the magnetic field in the reactor (forward field or reverse field). Note that these terms represent the only direct coupling between parallel and perpendicular kinetic energies. However, energy could also be transferred between them by the mediation of the ion and electron thermal energy. Furthermore, it is very possible that the parallel kinetic energy dynamics implicitly impacts the turbulence, for example by its impact on or competition with other energy transfer channels.
The interpretation of the other terms in the parallel kinetic energy equations (4.14) and (4.15) is rather standard and deviates little from that for the kinetic energy in hydrodynamic turbulence. The terms on the left-hand side under the divergence represent kinetic energy fluxes due to mean-field convection, turbulent convection and viscous transport. On the right-hand side, the first term is the viscous dissipation of kinetic energy which is converted into ion thermal energy. The second term contains RSs acting on the gradients of the parallel (ion) velocity and exchanges energy between turbulent and mean-field parallel kinetic energy again. The third term is the work done by the pressure gradient on the parallel velocity. Both for mean-field and turbulent energy this exchanges energy with the ion and electron thermal energy. This energy transfer might again take place in either direction. The last three terms are due to particle and momentum sources, which are expected to be mainly due to plasma–neutral interactions.
Finally, the last three terms on the right-hand side of the perpendicular turbulent kinetic energy equation (4.11) are due to particle and momentum sources in the plasma. The prime particle and momentum sources in the plasma are expected to be due to the ionisation of neutral particles and collisions with neutrals. These source terms are again closure terms, about which very limited information is available a priori.
Now, all source/sink terms on the right-hand side of the energy equations (3.8), (3.9), (4.10), (4.11), (4.14), (4.15), (4.24) and (4.25) appear in two equations with opposite signs, hence conserving their total energy. The energetic couplings between the different energy forms in plasma edge turbulence are illustrated in figure 1. The figure aims to give an overview of some of the couplings which are expected to be important, but does not contain all the energy transfer channels. This figure is inspired by a similar figure in Scott (Reference Scott2003).

Figure 1. Schematic representation of the main energy transfer channels between the different energy forms in plasma edge turbulence. Adapted from Scott (Reference Scott2003).
5. Decomposition of perpendicular kinetic energy equations
At this point, it is important to recall (cf. § 3) that mainly the turbulent fluxes $\boldsymbol {\varGamma }_{n,t,E}$![]() , $\boldsymbol {\varGamma }_{p_{{i}},t,E}$
, $\boldsymbol {\varGamma }_{p_{{i}},t,E}$![]() and $\boldsymbol {\varGamma }_{p_{{e}},t,E}$
and $\boldsymbol {\varGamma }_{p_{{e}},t,E}$![]() (see (3.15a–c) and (3.15a–c)) due to the $E\times B$
(see (3.15a–c) and (3.15a–c)) due to the $E\times B$![]() drift require modelling. It could be expected that these $E\times B$
drift require modelling. It could be expected that these $E\times B$![]() fluxes are more closely related to the turbulent kinetic energy in the $E\times B$
fluxes are more closely related to the turbulent kinetic energy in the $E\times B$![]() velocity fluctuation only than to the total turbulent kinetic energy due to the total perpendicular $\boldsymbol {V}_{0,\perp }$
velocity fluctuation only than to the total turbulent kinetic energy due to the total perpendicular $\boldsymbol {V}_{0,\perp }$![]() consisting of both the $E\times B$
consisting of both the $E\times B$![]() and the ion diamagnetic velocity. As such, this section will derive an equation for the kinetic energy in the $E\times B$
and the ion diamagnetic velocity. As such, this section will derive an equation for the kinetic energy in the $E\times B$![]() drift velocity only. In addition, equations for the energy in the diamagnetic drift velocity will likewise be derived.
drift velocity only. In addition, equations for the energy in the diamagnetic drift velocity will likewise be derived.
5.1. The $E\times B$ -only kinetic energy equations
-only kinetic energy equations
In analogy to the total kinetic energies, we define the $E\times B$![]() -only kinetic energies as
-only kinetic energies as
An equation for $E_{{E}}$![]() is likewise derived starting from the charge balance equation (4.3), as was done to obtain the equation for $E_{{k},\perp }$
is likewise derived starting from the charge balance equation (4.3), as was done to obtain the equation for $E_{{k},\perp }$![]() . However, the diamagnetic drift contribution to the polarisation current is now kept separate in the equivalent to (4.4)
. However, the diamagnetic drift contribution to the polarisation current is now kept separate in the equivalent to (4.4)
where the decomposition of $\boldsymbol {J}_{p}$![]() introduced in (2.9) and (2.13) is used. In analogy to expression (4.5), the second term on the right-hand side in the previous expression yields the time rate of change of the $E\times B$
introduced in (2.9) and (2.13) is used. In analogy to expression (4.5), the second term on the right-hand side in the previous expression yields the time rate of change of the $E\times B$![]() -only kinetic energy
-only kinetic energy

Filling out expressions (5.2)–(5.3) together with the manipulation (4.6) derived before into (4.3), the equation for $E_{{E}}$![]() is finally obtained
is finally obtained

The form of this equation is very similar to (4.7). However, $E_{{k},\perp }$![]() is ‘replaced’ by $E_{{E}}$
is ‘replaced’ by $E_{{E}}$![]() and $\boldsymbol {V}_{0,\perp }$
and $\boldsymbol {V}_{0,\perp }$![]() by $\boldsymbol {V}_{E}$
by $\boldsymbol {V}_{E}$![]() . Furthermore, the $\boldsymbol {\nabla }p_{{i}}\boldsymbol {\cdot }\boldsymbol {V}_{p}$
. Furthermore, the $\boldsymbol {\nabla }p_{{i}}\boldsymbol {\cdot }\boldsymbol {V}_{p}$![]() term is no longer present in the equation, while the last term on the right-hand side of (5.2) comes in to include the diamagnetic drift contribution to the polarisation current. Thus the latter is not neglected. Instead, it is chosen to account for it as a current divergence term instead of including it in the kinetic energy on the left-hand side, as was done in the total kinetic energy case in § 4.1. When the diamagnetic drift contribution to the polarisation current is small or is neglected, the $\phi \boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {J}_{p,*}$
term is no longer present in the equation, while the last term on the right-hand side of (5.2) comes in to include the diamagnetic drift contribution to the polarisation current. Thus the latter is not neglected. Instead, it is chosen to account for it as a current divergence term instead of including it in the kinetic energy on the left-hand side, as was done in the total kinetic energy case in § 4.1. When the diamagnetic drift contribution to the polarisation current is small or is neglected, the $\phi \boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {J}_{p,*}$![]() term can also be neglected. On the other hand, it is worth noting that the DW and interchange terms remain unchanged between the total perpendicular and the $E\times B$
term can also be neglected. On the other hand, it is worth noting that the DW and interchange terms remain unchanged between the total perpendicular and the $E\times B$![]() -only kinetic energy equations. Note that (5.4) could of course also have been derived directly from (4.7) by algebraic manipulation. This derivation proved, however, much more tortuous and tedious.
-only kinetic energy equations. Note that (5.4) could of course also have been derived directly from (4.7) by algebraic manipulation. This derivation proved, however, much more tortuous and tedious.
A mean-field $E\times B$![]() -only kinetic energy equation is derived by starting from (4.8) again. Applying analogous averaging operations as used in § 4.1 to the derivation made just before for the total $E\times B$
-only kinetic energy equation is derived by starting from (4.8) again. Applying analogous averaging operations as used in § 4.1 to the derivation made just before for the total $E\times B$![]() kinetic energy, we find
kinetic energy, we find

Taking the difference between the average of (5.4) and (5.5) again yields an equation for the turbulent kinetic energy, in the $E\times B$![]() drift fluctuations this time
drift fluctuations this time

Comparing these $E\times B$![]() -only kinetic energy equations (5.5) and (5.6) with the total perpendicular kinetic energy equations (4.10) and (4.11), the same changes as for the total kinetic energy can be observed. In addition, it is worth remarking that the RSs (second term on the right-hand side) have also changed now, in the sense that these now include only the $E\times B$
-only kinetic energy equations (5.5) and (5.6) with the total perpendicular kinetic energy equations (4.10) and (4.11), the same changes as for the total kinetic energy can be observed. In addition, it is worth remarking that the RSs (second term on the right-hand side) have also changed now, in the sense that these now include only the $E\times B$![]() velocity (and $\boldsymbol {V}_{C}$
velocity (and $\boldsymbol {V}_{C}$![]() ). Likewise, in the Favre averaging term (seventh term on the right-hand side) the diamagnetic drift polarisation current is no longer present.
). Likewise, in the Favre averaging term (seventh term on the right-hand side) the diamagnetic drift polarisation current is no longer present.
5.2. Ion-diamagnetic-drift-only kinetic energy equations
To complement the equations for the $E\times B$![]() -energy and to deepen the energy theorem, we derive equations for the kinetic energy in the ion diamagnetic drift in this section and in the ‘mixed’ $E\times B$
-energy and to deepen the energy theorem, we derive equations for the kinetic energy in the ion diamagnetic drift in this section and in the ‘mixed’ $E\times B$![]() -ion diamagnetic kinetic energy in the next section. The total, mean-field and turbulent diamagnetic kinetic energies are defined as
-ion diamagnetic kinetic energy in the next section. The total, mean-field and turbulent diamagnetic kinetic energies are defined as
In analogy to (4.5) and (5.3), a transport relation for the total kinetic energy in the diamagnetic drift velocity can be obtained as

Slightly rewriting readily yields the total diamagnetic kinetic energy equation as

An analogous derivation starting from $\boldsymbol {\nabla }_{\perp }\bar {p}_i\boldsymbol {\cdot }(\tilde {\boldsymbol {V}}_{p,*}+\tilde {\boldsymbol {V}}_{p,\varPi } + \tilde {\boldsymbol {V}}_{p,\|})$![]() yields an equation for the mean-field kinetic energy in the diamagnetic drift velocity
yields an equation for the mean-field kinetic energy in the diamagnetic drift velocity

Taking the difference between the average of (5.9) and (5.10), an equation for the turbulent diamagnetic kinetic energy is obtained

5.3. Mixed kinetic energy equations
At this point, it is important to remark that the sum of the $E\times B$![]() -only kinetic energy (see definition (5.1a–c)) and the ion-diamagnetic-drift-only kinetic energy (see definition (5.7a–c)) is not equal to the total perpendicular kinetic energy (see definition (4.1a–c)). Decomposing the total perpendicular kinetic energy as
-only kinetic energy (see definition (5.1a–c)) and the ion-diamagnetic-drift-only kinetic energy (see definition (5.7a–c)) is not equal to the total perpendicular kinetic energy (see definition (4.1a–c)). Decomposing the total perpendicular kinetic energy as

it is noted that there is a kinetic energy contribution from the ‘mixed’ $E\times B$![]() -ion diamagnetic kinetic energy. We define this mixed kinetic energy as
-ion diamagnetic kinetic energy. We define this mixed kinetic energy as
Note that these mixed kinetic energies can be negative when $\boldsymbol {V}_{E}$![]() and $\boldsymbol {V}_{*,i}$
and $\boldsymbol {V}_{*,i}$![]() are counter-aligned. As such, the term ‘energy’ might strictly speaking be somewhat of a misnomer.
are counter-aligned. As such, the term ‘energy’ might strictly speaking be somewhat of a misnomer.
According to (5.12), an equation for the total mixed kinetic energy can be calculated as the difference between (4.7) and (5.4) and (5.9). Likewise, an equation for the mean-field mixed kinetic energy is obtained from the difference between (4.10) and (5.5) and (5.10), and for the turbulent mixed kinetic energy from the difference between equation (4.11) and equations (5.6) and (5.11). This then yields


5.4. Refined energy theorem
The sources and sinks on the right-hand side of (5.4)–(5.6), (5.9)–(5.11) and (5.14)–(5.16) again represent the energetic couplings between the different energy equations. Firstly, this shows that the interchange and DW terms really transfer energy with the $E\times B$![]() kinetic energy only, and not with the other perpendicular kinetic energy contributions. The viscous stresses, on the other hand, transfer energy between the ion thermal energy (3.8) and the $E\times B$
kinetic energy only, and not with the other perpendicular kinetic energy contributions. The viscous stresses, on the other hand, transfer energy between the ion thermal energy (3.8) and the $E\times B$![]() -only and diamagnetic kinetic energy individually, acting on the respective velocities of the latter. The kinetic energy source due to momentum sources and the $\textrm {D}\boldsymbol {b}/\textrm {D} t$
-only and diamagnetic kinetic energy individually, acting on the respective velocities of the latter. The kinetic energy source due to momentum sources and the $\textrm {D}\boldsymbol {b}/\textrm {D} t$![]() terms are likewise split between both forms of kinetic energy. The kinetic energy source due to the particle source acts independently on all three kinds of kinetic energy.
terms are likewise split between both forms of kinetic energy. The kinetic energy source due to the particle source acts independently on all three kinds of kinetic energy.
In addition, the pressure work on the polarisation velocity exchanges energy between the ion thermal energy and $E_{*}$![]() and $E_{\mathrm {mix}}$
and $E_{\mathrm {mix}}$![]() separately. Thus, it can be seen that, somewhat surprisingly, the diamagnetic kinetic energy equation is not directly coupled to the other perpendicular kinetic energy equations at all. Then, the $\boldsymbol {\nabla }\phi \boldsymbol {\cdot }\boldsymbol {J}_{p,*}$
separately. Thus, it can be seen that, somewhat surprisingly, the diamagnetic kinetic energy equation is not directly coupled to the other perpendicular kinetic energy equations at all. Then, the $\boldsymbol {\nabla }\phi \boldsymbol {\cdot }\boldsymbol {J}_{p,*}$![]() term exchanges energy between $E_{{E}}$
term exchanges energy between $E_{{E}}$![]() and $E_{\mathrm {mix}}$
and $E_{\mathrm {mix}}$![]() . Thus, the latter ‘mixed’ form of kinetic energy exchanges energy with the ion thermal energy and the $E\times B$
. Thus, the latter ‘mixed’ form of kinetic energy exchanges energy with the ion thermal energy and the $E\times B$![]() kinetic energy.
kinetic energy.
Lastly, the various forms of the RS and Favre terms exchange energy between the mean-field kinetic energy equation and the corresponding turbulent kinetic energy equation.
The fact that the interchange and DW mechanisms, generally assumed to be the main turbulence drives in the plasma edge, exchange energy with the $E\times B$![]() energy only, seems to be in line with the $E\times B$
energy only, seems to be in line with the $E\times B$![]() fluctuations being stronger than the diamagnetic ones. Moreover, the diamagnetic and mixed kinetic energies have much less (direct) couplings, especially to the thermal energy reservoirs which are supposedly the most important ones. This could be expected to further limit the strength of the turbulence in these components. It is particularly interesting to observe that only the $E\times B$
fluctuations being stronger than the diamagnetic ones. Moreover, the diamagnetic and mixed kinetic energies have much less (direct) couplings, especially to the thermal energy reservoirs which are supposedly the most important ones. This could be expected to further limit the strength of the turbulence in these components. It is particularly interesting to observe that only the $E\times B$![]() kinetic energy is coupled to the electron thermal energy and to the magnetic energy.
kinetic energy is coupled to the electron thermal energy and to the magnetic energy.
Figure 2 shows a schematic representation of the energy couplings split out over the different components of the perpendicular kinetic energy. Note that the contributions presumed to be important that were shown in figure 1 are actually all between the $E\times B$![]() -only kinetic energy and other energy forms, never involving the diamagnetic or mixed kinetic energy. As such, we do not put the mathematical expressions for the couplings of the $E\times B$
-only kinetic energy and other energy forms, never involving the diamagnetic or mixed kinetic energy. As such, we do not put the mathematical expressions for the couplings of the $E\times B$![]() -only kinetic energy (indicated with green arrows) in figure 2 since they were already denoted in figure 1.
-only kinetic energy (indicated with green arrows) in figure 2 since they were already denoted in figure 1.

Figure 2. Schematic representation of the energy transfer channels between the different perpendicular kinetic energy forms in plasma edge turbulence.
6. Towards a turbulence closure model
The general framework of mean-field equations and the strategy to be followed for their closure presented in the previous sections made no assumptions on the dimensionality of the turbulence. However, earlier work has largely focused on purely 2-D plasma edge turbulence, accounting for the parallel direction through approximate volumetric sinks (Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2020, Reference Coosemans, Dekeyser and Baelmans2021a,Reference Coosemans, Dekeyser and Baelmansb, Reference Coosemans, Dekeyser and Baelmans2022). While this allowed us to gain valuable insights into the basic dynamics of the perpendicular turbulent transport, the considered cases were still rather far from a reactor relevant case. Reducing the assumptions compared with this earlier work as well as compared with Scott (Reference Scott2003) leads to a more complex set of mean-field equations. However, we would like to stress that the final model for the closure terms should not necessarily include all the new terms that are identified. The full set should only be used to check which terms do need to make it into the final reduced mean-field model. On the other hand, a reduced model can only be expected to approximate reality when it takes into account all the relevant terms. Nonetheless, it is expected that the basic physics modelled for the reduced cases can be extrapolated to more complex cases to some extent. This section will look ahead considering the implications of the models developed earlier in view of the general mean-field equations presented here for mean-field transport in general and discuss the elements of the model that require further refinement.
6.1. Modelling mean-field turbulent fluxes
Section 3 established that the average turbulent $E\times B$![]() particle flux $\boldsymbol {\varGamma }_{n,t,E}$
particle flux $\boldsymbol {\varGamma }_{n,t,E}$![]() in the average continuity equation (3.6) or (3.7) and heat fluxes $\boldsymbol {\varGamma }_{p_{{i}},t,E}$
in the average continuity equation (3.6) or (3.7) and heat fluxes $\boldsymbol {\varGamma }_{p_{{i}},t,E}$![]() and $\boldsymbol {\varGamma }_{p_{{e}},t,E}$
and $\boldsymbol {\varGamma }_{p_{{e}},t,E}$![]() in the thermal energy equations (3.8) and (3.9) are vital closure terms to be modelled. Following the common practise in mean-field transport modelling (LaBombard et al. Reference LaBombard, Umansky, Boivin, Goetz, Hughes, Lipschultz, Mossessian, Pitcher and Terry2000; Aho-Mantila et al. Reference Aho-Mantila, Wischmeier, Müller, Potzel, Coster, Bonnin and Conway2012; Reimold et al. Reference Reimold, Wischmeier, Bernert, Potzel, Coster, Bonnin, Reiter, Meisl, Kallenbach and Aho-Mantila2015; Dekeyser et al. Reference Dekeyser, Bonnin, Lisgo, Pitts, Brunner, LaBombard and Terry2016), Coosemans et al. (Reference Coosemans, Dekeyser and Baelmans2020, Reference Coosemans, Dekeyser and Baelmans2021a,Reference Coosemans, Dekeyser and Baelmansb, Reference Coosemans, Dekeyser and Baelmans2022) suggested to model these fluxes through diffusion relations
in the thermal energy equations (3.8) and (3.9) are vital closure terms to be modelled. Following the common practise in mean-field transport modelling (LaBombard et al. Reference LaBombard, Umansky, Boivin, Goetz, Hughes, Lipschultz, Mossessian, Pitcher and Terry2000; Aho-Mantila et al. Reference Aho-Mantila, Wischmeier, Müller, Potzel, Coster, Bonnin and Conway2012; Reimold et al. Reference Reimold, Wischmeier, Bernert, Potzel, Coster, Bonnin, Reiter, Meisl, Kallenbach and Aho-Mantila2015; Dekeyser et al. Reference Dekeyser, Bonnin, Lisgo, Pitts, Brunner, LaBombard and Terry2016), Coosemans et al. (Reference Coosemans, Dekeyser and Baelmans2020, Reference Coosemans, Dekeyser and Baelmans2021a,Reference Coosemans, Dekeyser and Baelmansb, Reference Coosemans, Dekeyser and Baelmans2022) suggested to model these fluxes through diffusion relations
and to relate the effective turbulent transport coefficients $D$![]() , $\chi _i$
, $\chi _i$![]() and $\chi _e$
and $\chi _e$![]() to characteristic quantities for the turbulence, i.e. $D=D(k_{E},\zeta _{E},\ldots )$
to characteristic quantities for the turbulence, i.e. $D=D(k_{E},\zeta _{E},\ldots )$![]() , $\chi _e=\chi _e(k_{E},\zeta _{E},\ldots )$
, $\chi _e=\chi _e(k_{E},\zeta _{E},\ldots )$![]() , $\chi _i=\chi _i(k_{E},\zeta _{E},\ldots )$
, $\chi _i=\chi _i(k_{E},\zeta _{E},\ldots )$![]() . Coosemans et al. (Reference Coosemans, Dekeyser and Baelmans2022) found that the three transport coefficient are proportional to one another up to a constant of order unity for the investigated 2-D, electrostatic, interchange-dominated, sheath-connected SOL cases. It remains to be confirmed if this scaling holds more generally. For now, it is assumed that this results holds to a certain extent in more complex cases as well. It stands to reason to propose a similar diffusion relation for the turbulent $E\times B$
. Coosemans et al. (Reference Coosemans, Dekeyser and Baelmans2022) found that the three transport coefficient are proportional to one another up to a constant of order unity for the investigated 2-D, electrostatic, interchange-dominated, sheath-connected SOL cases. It remains to be confirmed if this scaling holds more generally. For now, it is assumed that this results holds to a certain extent in more complex cases as well. It stands to reason to propose a similar diffusion relation for the turbulent $E\times B$![]() flux of parallel momentum
flux of parallel momentum
and to assume that $\nu \sim D$![]() as well.
as well.
Under these assumptions, it suffices to model only one of the transport coefficients to obtain a model for all four. Drawing on Coosemans et al. (Reference Coosemans, Dekeyser and Baelmans2020, Reference Coosemans, Dekeyser and Baelmans2021a,Reference Coosemans, Dekeyser and Baelmansb, Reference Coosemans, Dekeyser and Baelmans2022) and Coosemans (Reference Coosemans2022), an elaborate scaling of the form
may be suggested. The philosophy of this model is that $k_{E}$![]() provides a velocity scale for the turbulence, while the enstrophy $\zeta _{E}$
provides a velocity scale for the turbulence, while the enstrophy $\zeta _{E}$![]() and the flow shear rate $S_{m}$
and the flow shear rate $S_{m}$![]() provide competing time scales for the turbulence. Finally, the effective phase difference between the density and potential fluctuations $\varPsi$
provide competing time scales for the turbulence. Finally, the effective phase difference between the density and potential fluctuations $\varPsi$![]() provides an additional correction. This phase difference is typically a characteristic of the turbulent regime, and could presumably be modelled based on which terms are (locally) dominant in the $k_{E}$
provides an additional correction. This phase difference is typically a characteristic of the turbulent regime, and could presumably be modelled based on which terms are (locally) dominant in the $k_{E}$![]() equation. It might still be necessary to adjust the coefficients $C_D$
equation. It might still be necessary to adjust the coefficients $C_D$![]() and/or $C_S$
and/or $C_S$![]() depending on the turbulence regime (open or closed field lines, interchange- or DW-dominated case, sheath connected or not). This transport coefficient model, how general it is and how far case-specific parameter tuning is needed, certainly require further investigation in realistic 3-D cases. However, given its rather robust performance in Coosemans et al. (Reference Coosemans, Dekeyser and Baelmans2021b, Reference Coosemans, Dekeyser and Baelmans2022), it seems reasonable to assume that the basic scaling
depending on the turbulence regime (open or closed field lines, interchange- or DW-dominated case, sheath connected or not). This transport coefficient model, how general it is and how far case-specific parameter tuning is needed, certainly require further investigation in realistic 3-D cases. However, given its rather robust performance in Coosemans et al. (Reference Coosemans, Dekeyser and Baelmans2021b, Reference Coosemans, Dekeyser and Baelmans2022), it seems reasonable to assume that the basic scaling
will hold to some extent, even though the proportionality factor may not take a strictly fixed value that works for all cases. Assuming that this scaling holds, the next section will summarise the progress that has been made in modelling the transport equation of $k_{E}$![]() , and which terms and effects require further attention. Besides the relevance for the transport coefficients themselves, this also led to insights into the dynamics and drivers of the turbulence itself.
, and which terms and effects require further attention. Besides the relevance for the transport coefficients themselves, this also led to insights into the dynamics and drivers of the turbulence itself.
6.2. Modelling the turbulent kinetic energy equation
The general $E\times B$![]() turbulent kinetic energy equation for a low $\beta$
turbulent kinetic energy equation for a low $\beta$![]() edge plasma has been derived in § 5.1 as (5.6). We start by simplifying this equation ignoring a number of terms presumed to be of minor importance
edge plasma has been derived in § 5.1 as (5.6). We start by simplifying this equation ignoring a number of terms presumed to be of minor importance

Firstly, the sum of the transport terms $\boldsymbol {\nabla }\boldsymbol {\cdot }(\overline {\phi '\boldsymbol {J}_{\perp }'}+\overline {p'\boldsymbol {V}_{E}'})$![]() has been neglected. Even though each of these terms individually may be large, Scott (Reference Scott2003) argues that their sum is small due to Poynting cancellation. Moreover, under a low $\beta$
has been neglected. Even though each of these terms individually may be large, Scott (Reference Scott2003) argues that their sum is small due to Poynting cancellation. Moreover, under a low $\beta$![]() approximation the subterm $\boldsymbol {\nabla }\boldsymbol {\cdot }(\overline {\phi '\boldsymbol {J}_{*}'}+\overline {p'\boldsymbol {V}_{E}'})=\boldsymbol {\nabla }\boldsymbol {\cdot }(\boldsymbol {\nabla }(\overline {p'\phi '})\times \boldsymbol {b}/B)$
approximation the subterm $\boldsymbol {\nabla }\boldsymbol {\cdot }(\overline {\phi '\boldsymbol {J}_{*}'}+\overline {p'\boldsymbol {V}_{E}'})=\boldsymbol {\nabla }\boldsymbol {\cdot }(\boldsymbol {\nabla }(\overline {p'\phi '})\times \boldsymbol {b}/B)$![]() can be shown to depend solely on magnetic field gradients, of which the length scale is supposed to be much larger than the turbulent length scale (Scott Reference Scott2003; Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2021b). Next, the terms involving the viscous stresses have likewise been neglected. On evaluations of this $k_{E}$
can be shown to depend solely on magnetic field gradients, of which the length scale is supposed to be much larger than the turbulent length scale (Scott Reference Scott2003; Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2021b). Next, the terms involving the viscous stresses have likewise been neglected. On evaluations of this $k_{E}$![]() equation for simplified TOKAM2D cases, these terms were observed to always play a secondary role (Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2020, Reference Coosemans, Dekeyser and Baelmans2021b, Reference Coosemans, Dekeyser and Baelmans2022). This complies with the general assumption that plasma edge turbulence is dominated by an inviscid dynamics (Camargo et al. Reference Camargo, Biskamp and Scott1995). Lastly, the Favre term has likewise been left away since all earlier TOKAM2D results showed it to be small as well.
equation for simplified TOKAM2D cases, these terms were observed to always play a secondary role (Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2020, Reference Coosemans, Dekeyser and Baelmans2021b, Reference Coosemans, Dekeyser and Baelmans2022). This complies with the general assumption that plasma edge turbulence is dominated by an inviscid dynamics (Camargo et al. Reference Camargo, Biskamp and Scott1995). Lastly, the Favre term has likewise been left away since all earlier TOKAM2D results showed it to be small as well.
The interchange term (second term on the right-hand side of (6.5)) is widely accepted to act like the major drive of the turbulence in the SOL on the low field side (LFS) in many cases. A general analytical equation has been derived for this term by Coosemans et al. (Reference Coosemans, Dekeyser and Baelmans2021b, Reference Coosemans, Dekeyser and Baelmans2022). This starts by rewriting (Scott Reference Scott2003)
where the second term can be neglected by a low-$\beta$![]() approximation. Rewriting the fluctuations and using the definitions of the $E\times B$
approximation. Rewriting the fluctuations and using the definitions of the $E\times B$![]() particle and heat fluxes in (3.15a–c) and (3.15a–c), it is found that (Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2022)
particle and heat fluxes in (3.15a–c) and (3.15a–c), it is found that (Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2022)

Hence, if closure models are available for the $E\times B$![]() fluxes, whether of the form suggested in § 6.1 or not, the interchange source of $k_{E}$
fluxes, whether of the form suggested in § 6.1 or not, the interchange source of $k_{E}$![]() can be evaluated analytically. This provides a very convenient ingredient for a closure model. Moreover, it also automatically induces a ballooning character into a turbulent transport model as already remarked in earlier publications (Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2020, Reference Coosemans, Dekeyser and Baelmans2021b, Reference Coosemans, Dekeyser and Baelmans2022). Indeed, the turbulent heat fluxes will normally be outward everywhere, while the magnetic field gradient is only opposed to this flux on the LFS. As a result, the interchange term tends to act like a source on the LFS, while it acts like a sink on the high field side (HFS). This behaviour has been confirmed in 2-D mean-field simulations with SOLPS-ITER in which a model based on the $k_{\perp }$
can be evaluated analytically. This provides a very convenient ingredient for a closure model. Moreover, it also automatically induces a ballooning character into a turbulent transport model as already remarked in earlier publications (Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2020, Reference Coosemans, Dekeyser and Baelmans2021b, Reference Coosemans, Dekeyser and Baelmans2022). Indeed, the turbulent heat fluxes will normally be outward everywhere, while the magnetic field gradient is only opposed to this flux on the LFS. As a result, the interchange term tends to act like a source on the LFS, while it acts like a sink on the high field side (HFS). This behaviour has been confirmed in 2-D mean-field simulations with SOLPS-ITER in which a model based on the $k_{\perp }$![]() equation presented here has been implemented (Dekeyser et al. Reference Dekeyser, Coosemans, Carli and Baelmans2022). Note that this interchange model holds in general and is thus not only relevant in interchange-dominated turbulence regimes. It is interesting to remark that, even when another term would provide a more poloidally uniform drive of $k_{\perp }$
equation presented here has been implemented (Dekeyser et al. Reference Dekeyser, Coosemans, Carli and Baelmans2022). Note that this interchange model holds in general and is thus not only relevant in interchange-dominated turbulence regimes. It is interesting to remark that, even when another term would provide a more poloidally uniform drive of $k_{\perp }$![]() , the turbulence on the HFS would be decreased and that on the LFS increased due to the resulting turbulent $E\times B$
, the turbulence on the HFS would be decreased and that on the LFS increased due to the resulting turbulent $E\times B$![]() heat fluxes.
heat fluxes.
In sheath-connected interchange-dominated LFS SOL cases studied with the TOKAM2D code, it was found that this interchange term is balanced by the parallel loss to the sheath (Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2020, Reference Coosemans, Dekeyser and Baelmans2021b, Reference Coosemans, Dekeyser and Baelmans2022). This term is the equivalent of the transport part of the parallel current contribution (fourth term on the left-hand side of (6.5)). It was also found that the underlying ‘anomalous’ parallel flux $\overline {\phi '\boldsymbol {J}_{\|}'}$![]() largely exceeds the equivalent of the mean-field and the turbulent parallel convection.
largely exceeds the equivalent of the mean-field and the turbulent parallel convection.
This has interesting implications for the distribution of $k_{\perp }$![]() in tokamaks. The exploratory SOLPS-ITER case presented by Dekeyser et al. (Reference Dekeyser, Coosemans, Carli and Baelmans2022) had the interchange term as the dominant source of $k_{\perp }$
in tokamaks. The exploratory SOLPS-ITER case presented by Dekeyser et al. (Reference Dekeyser, Coosemans, Carli and Baelmans2022) had the interchange term as the dominant source of $k_{\perp }$![]() with this fast transport acting like the main compensation mechanism. The resulting balance showed strong production of turbulence around the outer midplane (OMP), which is quickly removed by the fast parallel transport. In the SOL, this allows saturation of the turbulence by removal of $k_{\perp }$
with this fast transport acting like the main compensation mechanism. The resulting balance showed strong production of turbulence around the outer midplane (OMP), which is quickly removed by the fast parallel transport. In the SOL, this allows saturation of the turbulence by removal of $k_{\perp }$![]() to the divertor targets, which is reminiscent of the physics of the TOKAM2D cases. In the core region, on the other hand, $k_{\perp }$
to the divertor targets, which is reminiscent of the physics of the TOKAM2D cases. In the core region, on the other hand, $k_{\perp }$![]() can be transported away from the OMP to the HFS, where it may be dissipated by the interchange term acting like a sink in that region. Hence, this term adds a strongly non-local element to the balance of $k_{\perp }$
can be transported away from the OMP to the HFS, where it may be dissipated by the interchange term acting like a sink in that region. Hence, this term adds a strongly non-local element to the balance of $k_{\perp }$![]() and thus to the turbulent transport of particles and heat. Furthermore, this increased parallel spreading of $k_{\perp }$
and thus to the turbulent transport of particles and heat. Furthermore, this increased parallel spreading of $k_{\perp }$![]() also means that the resulting turbulent transport is less ballooned than would have been the case had the interchange source (on the LFS) been balanced by a local sink. More research, however, is needed to develop a reliable model for this anomalous parallel flux.
also means that the resulting turbulent transport is less ballooned than would have been the case had the interchange source (on the LFS) been balanced by a local sink. More research, however, is needed to develop a reliable model for this anomalous parallel flux.
It is not claimed in this article that this flow picture or the corresponding saturation mechanism is generally valid in any tokamak operating regime. Nonetheless, the insights provided by them and the role of the $\overline {\phi '\boldsymbol {J}_{\|}'}$![]() flux in enhancing the parallel spreading of the turbulence are believed to be novel and may in general be considered in the overall flow picture in tokamaks. Many other effects which were not yet taken into account may, however, modify this dynamics.
flux in enhancing the parallel spreading of the turbulence are believed to be novel and may in general be considered in the overall flow picture in tokamaks. Many other effects which were not yet taken into account may, however, modify this dynamics.
6.3. Limitations of the $k_{\perp }$ model
model
In the current stage of its development, the validity of the $k_{\perp }$![]() model as presented by Coosemans et al. (Reference Coosemans, Dekeyser and Baelmans2022) and Dekeyser et al. (Reference Dekeyser, Coosemans, Carli and Baelmans2022) is limited since it has mostly been developed and tested for 2-D, interchange-dominated, sheath-connected, electrostatic SOL cases. A number of terms which are expected to be important in the $k_{E}$
model as presented by Coosemans et al. (Reference Coosemans, Dekeyser and Baelmans2022) and Dekeyser et al. (Reference Dekeyser, Coosemans, Carli and Baelmans2022) is limited since it has mostly been developed and tested for 2-D, interchange-dominated, sheath-connected, electrostatic SOL cases. A number of terms which are expected to be important in the $k_{E}$![]() transport equation (6.5) in different cases were neglected.
transport equation (6.5) in different cases were neglected.
The first and third terms in (6.5) associated with the DW and RS energy transfer channel (see § 4.4) have for example not yet been duly modelled, even though they are expected to be of primary importance for many machine-relevant cases. The exact form of these terms in the equation for $k_{E}$![]() in particular allows their further analysis in the context of the development of an improved $k_{\perp }$
in particular allows their further analysis in the context of the development of an improved $k_{\perp }$![]() model. From a preliminary analysis for a limited number of cases in Coosemans (Reference Coosemans2022), it seems that the DW term can change significantly depending on the regime the turbulence is in and how exactly the competition with other terms occurs. Much more analysis is thus required to model this term.
model. From a preliminary analysis for a limited number of cases in Coosemans (Reference Coosemans2022), it seems that the DW term can change significantly depending on the regime the turbulence is in and how exactly the competition with other terms occurs. Much more analysis is thus required to model this term.
The RS term is expected to be of minor importance in the SOL because the flow shear is limited by the electrostatic potential being tied to the sheath potential at the end of the field lines. However, around the separatrix and in the core region, strong poloidal flows, which are sheared in the radial direction, may develop, such that the $m\overline {nV_{C,r}'V_{E,\theta }''}\partial _r\tilde {V}_{E,\theta }$![]() contribution in particular may become important. Primarily, this term is expected to break up the turbulent eddies and as such act like a sink of $k_{\perp }$
contribution in particular may become important. Primarily, this term is expected to break up the turbulent eddies and as such act like a sink of $k_{\perp }$![]() (in line with the inverse energy cascade Yakhot Reference Yakhot2004; Alexakis & Doering Reference Alexakis and Doering2006; Fundamenski Reference Fundamenski2010). However, when the turbulence is sufficiently damped and when the flow shear is sufficiently strong, the KH instability may come into play. This secondary instability might then lead the RS term to act like a source of $k_{\perp }$
(in line with the inverse energy cascade Yakhot Reference Yakhot2004; Alexakis & Doering Reference Alexakis and Doering2006; Fundamenski Reference Fundamenski2010). However, when the turbulence is sufficiently damped and when the flow shear is sufficiently strong, the KH instability may come into play. This secondary instability might then lead the RS term to act like a source of $k_{\perp }$![]() (Rogers & Dorland Reference Rogers and Dorland2005; Myra et al. Reference Myra, D'Ippolito, Russell, Umansky and Baver2016; Giacomin & Ricci Reference Giacomin and Ricci2020). Furthermore, as indicated in (6.3), strong flow shear could also influence the diffusion relation itself. Hence, flow shear is expected to lead to both a reduction of $k_{E}$
(Rogers & Dorland Reference Rogers and Dorland2005; Myra et al. Reference Myra, D'Ippolito, Russell, Umansky and Baver2016; Giacomin & Ricci Reference Giacomin and Ricci2020). Furthermore, as indicated in (6.3), strong flow shear could also influence the diffusion relation itself. Hence, flow shear is expected to lead to both a reduction of $k_{E}$![]() and a reduction of the transport coefficients at the same $k_{E}$
and a reduction of the transport coefficients at the same $k_{E}$![]() . In addition, since both effects depend on the flow shear, a model for $\partial _r\tilde {V}_{E,\theta }$
. In addition, since both effects depend on the flow shear, a model for $\partial _r\tilde {V}_{E,\theta }$![]() itself is required. While the mean-field $E\times B$
itself is required. While the mean-field $E\times B$![]() velocity can be calculated from the mean-field charge balance equation (3.12) for the electrostatic potential, the closure terms in this equation need further attention.
velocity can be calculated from the mean-field charge balance equation (3.12) for the electrostatic potential, the closure terms in this equation need further attention.
Furthermore, the effects of perpendicular turbulent transport of $k_{E}$![]() might also require further attention. In the TOKAM2D cases studied earlier, its contribution to the balance of $k_{\perp }$
might also require further attention. In the TOKAM2D cases studied earlier, its contribution to the balance of $k_{\perp }$![]() was found to be small. However, this may not be the case in general (Ghendrih et al. Reference Ghendrih, Sarazin, Ciraolo, Darmet, Garbet, Grangirard, Tamain, Benkadda and Beyer2007). In regions where the perpendicular gradients of $k_{\perp }$
was found to be small. However, this may not be the case in general (Ghendrih et al. Reference Ghendrih, Sarazin, Ciraolo, Darmet, Garbet, Grangirard, Tamain, Benkadda and Beyer2007). In regions where the perpendicular gradients of $k_{\perp }$![]() are steeper, more radial transport of it would likewise be expected (Singh & Diamond Reference Singh and Diamond2020). Such strong gradients are expected around the separatrix due to strong flow shear, and perhaps also in the divertor at the boundary between the private flux region and the SOL.
are steeper, more radial transport of it would likewise be expected (Singh & Diamond Reference Singh and Diamond2020). Such strong gradients are expected around the separatrix due to strong flow shear, and perhaps also in the divertor at the boundary between the private flux region and the SOL.
The phenomena included in the last five terms in (6.5) have been subject to far less study as far as the authors are aware. This makes it interesting to first evaluate these terms with detailed reference data, from turbulence code simulations for example. This way, either it could be found that they have rightfully not been given much consideration, or it might open the door to valuable new insights. In a next step, the relevant terms could then be modelled and incorporated in an extended $k_{\perp }$![]() model.
model.
The last three terms in (6.5) arise through (fluctuating) particle and momentum source terms. These source terms are expected to be mainly caused by plasma–neutral interactions. While these interactions have long been considered in mean-field transport modelling (Reiter Reference Reiter1992; Rognlien et al. Reference Rognlien, Ryutov, Mattor and Porter1999; Wiesen Reference Wiesen2006; Dekeyser Reference Dekeyser2014; Dekeyser et al. Reference Dekeyser, Reiter and Baelmans2014; Bufferand et al. Reference Bufferand, Ciraolo, Marandet, Bucalossi, Ghendrih, Gunn, Mellet, Tamain, Leybros and Fedorczak2015; Wiesen et al. Reference Wiesen, Reiter, Kotov, Baelmans, Dekeyser, Kukushkin, Lisgo, Pitts, Rozhansky and Saibene2015; Bonnin et al. Reference Bonnin, Dekeyser, Pitts, Coster, Voskoboynikov and Wiesen2016; Simonini et al. Reference Simonini, Corrigan, Radford, Spence and Taroni2018), their study in the context of edge turbulence and their integration in turbulence codes has only been picked up more recently (Marandet et al. Reference Marandet, Tamain, Futtersack, Ghendrih, Bufferand, Genesio and Mekkaoui2013; Wersal & Ricci Reference Wersal and Ricci2015; Thrysøea et al. Reference Thrysøea, Løiten, Madsen, Naulin, Nielsen and Rasmussen2018; Fan et al. Reference Fan, Marandet, Tamain, Bufferand, Ciraolo, Ghendrih and Serre2019; Bufferand et al. Reference Bufferand, Bucalossi, Ciraolo, Falchetto, Gallo, Ghendrih, Rivals, Tamain, Yang and Giorgiani2021; Zholobenko et al. Reference Zholobenko, Stegmeir, Griener, Conway, Body, Coster and Jenko2021; Giacomin et al. Reference Giacomin, Ricci, Coroado, Fourestey, Galassi, Lanti, Mancini, Richart, Stenger and Varini2022). While the recent results obtained show the neutrals to have an important influence on the turbulence, it remains to be established if the source terms identified in (6.5) are large (in certain regimes and regions), or whether their effect is more indirect.
Likewise, the literature has already found that including the contribution of the diamagnetic drift to the polarisation current changes the dynamics of the turbulence (Madsen et al. Reference Madsen, Garcia, Larsen, Naulin, Nielsen and Rasmussen2011; Bisai & Kaw Reference Bisai and Kaw2013; Baudoin Reference Baudoin2018). This contribution is taken into account in most modern turbulence codes, although Coosemans (Reference Coosemans2022) showed that care should be taken to not introduce unphysical terms when implementing this. However, this effect has not yet been duly studied in the context of source terms for $k_{E}$![]() (fourth term on the right-hand side of (6.5)). Again, further research should investigate if this term is large, or whether the influence of the inertia of the diamagnetic drift is through other (indirect) mechanisms. For this, the diamagnetic and mixed kinetic energy equations (5.11) and (5.16) might likewise be studied.
(fourth term on the right-hand side of (6.5)). Again, further research should investigate if this term is large, or whether the influence of the inertia of the diamagnetic drift is through other (indirect) mechanisms. For this, the diamagnetic and mixed kinetic energy equations (5.11) and (5.16) might likewise be studied.
Finally, the $\textrm {D}\boldsymbol {b}/\textrm {D} t$![]() term is commonly neglected in the polarisation current defined in (2.11) which enters in the charge balance equation (2.20) and in the parallel ion momentum equation (2.23). This is also the case in modern turbulence codes. As such, the energetic coupling between the parallel and perpendicular kinetic energy and the fifth term on the right-hand side of (6.5) is not taken into account in these codes. Being the only direct transfer channel between parallel and perpendicular kinetic energy and in particular coupling $k_{E}$
term is commonly neglected in the polarisation current defined in (2.11) which enters in the charge balance equation (2.20) and in the parallel ion momentum equation (2.23). This is also the case in modern turbulence codes. As such, the energetic coupling between the parallel and perpendicular kinetic energy and the fifth term on the right-hand side of (6.5) is not taken into account in these codes. Being the only direct transfer channel between parallel and perpendicular kinetic energy and in particular coupling $k_{E}$![]() with the mean-field parallel flows which are known to be large, it might be speculated to provide, however, a significant source of energy to the turbulence. Evaluating the $\textrm {D}\boldsymbol {b}/\textrm {D} t$
with the mean-field parallel flows which are known to be large, it might be speculated to provide, however, a significant source of energy to the turbulence. Evaluating the $\textrm {D}\boldsymbol {b}/\textrm {D} t$![]() term in the $k_{E}$
term in the $k_{E}$![]() equation (a posteriori) would allow to verify this assumption. If it were found to be important, it could allow to improve the accuracy of the turbulence codes. Later on, it could then be further studied and modelled for use in an extended $k_{\perp }$
equation (a posteriori) would allow to verify this assumption. If it were found to be important, it could allow to improve the accuracy of the turbulence codes. Later on, it could then be further studied and modelled for use in an extended $k_{\perp }$![]() model as well.
model as well.
Depending on which of the terms in the $k_{\perp }$![]() equation are dominant in a certain case, i.e. which regime the turbulence is in, it can be expected that the structure of the turbulence is different. As a result, it is likely that the exact relation between the intensity of the turbulence (e.g. $k_{\perp }$
equation are dominant in a certain case, i.e. which regime the turbulence is in, it can be expected that the structure of the turbulence is different. As a result, it is likely that the exact relation between the intensity of the turbulence (e.g. $k_{\perp }$![]() ) and the transport resulting from it (i.e. the turbulent transport coefficients) will be different. Hence, it is possible that depending on the regime, different model constants might be needed in (6.4) or even a different form of the transport relation itself. The occurrence of different turbulence regimes and the threshold values for the transition between them have been studied in the literature, see for example Scott (Reference Scott2005), Mosetto et al. (Reference Mosetto, Halpern, Jolliet, Loizu and Ricci2013), Giacomin & Ricci (Reference Giacomin and Ricci2020) and Eich et al. (Reference Eich and Manz2021).
) and the transport resulting from it (i.e. the turbulent transport coefficients) will be different. Hence, it is possible that depending on the regime, different model constants might be needed in (6.4) or even a different form of the transport relation itself. The occurrence of different turbulence regimes and the threshold values for the transition between them have been studied in the literature, see for example Scott (Reference Scott2005), Mosetto et al. (Reference Mosetto, Halpern, Jolliet, Loizu and Ricci2013), Giacomin & Ricci (Reference Giacomin and Ricci2020) and Eich et al. (Reference Eich and Manz2021).
Furthermore, models that are not purely diffusive for the turbulent fluxes could be of interest since the literature indicates that particle and heat transport in the plasma edge is in fact driven by radially propagating structures such as avalanches and blob filaments. They would rather induce intermittent convective/ballistic transport with a strong non-local character (Politzer et al. Reference Politzer, Austin, Gilmore, McKee, Rhodes, Yu, Doyle, Evans and Moyere2002; Garcia et al. Reference Garcia, Naulin, Nielsen and Rasmussen2006; Naulin Reference Naulin2007; Krasheninnikov, D'Ippolito & Myra Reference Krasheninnikov, D'Ippolito and Myra2008; Ghendrih et al. Reference Ghendrih, Ciraolo, Larmande, Sarazin, Tamain, Beyer, Chiavassa, Darmet, Garbet and Grandgirard2009; D'Ippolito, Myra & Zweben Reference D'Ippolito, Myra and Zweben2011). It might, however, be expected that a well-chosen diffusion model can give a reasonable approximation of the long time scale average particle flux caused by all the instantaneous filaments with high and low density structures moving respectively outward and inward in a seemingly random way. Note also that the models for the transport coefficients do not need to use local quantities only. The transport of $k_{E}$![]() introduces a non-local effect in the mean-field model for example. This transport allows turbulent kinetic energy created in one location to increase turbulent transport in another.
introduces a non-local effect in the mean-field model for example. This transport allows turbulent kinetic energy created in one location to increase turbulent transport in another.
Hence, it is expected that a basic scaling between the transport coefficients and well-chosen quantifiers of the turbulence can be used to get an idea of the characteristics of the transport. It has indeed been proven in earlier work (Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2020, Reference Coosemans, Dekeyser and Baelmans2021b, Reference Coosemans, Dekeyser and Baelmans2022) that such models can provide very accurate predictions for particular regimes such as electrostatic interchange-dominated $E\times B$![]() turbulence in a sheath-connected SOL.
turbulence in a sheath-connected SOL.
7. Conclusion
Recently, models incorporating information about turbulent quantities have been developed to self-consistently model the turbulent fluxes in mean-field transport codes. While these efforts seem to be relatively successful for the investigated cases, a complete theoretical set of basic equations to guide this model development had not yet been published.
This paper has addressed this issue by providing mean-field equations for the continuity equation, thermal energy equations, parallel momentum equations and charge balance equations through a rigorous averaging procedure applied to Braginskii-like equations underlying the plasma models of mean-field edge codes. This provides an exact interpretation in terms of fluctuations and averages of both the mean-field terms which are included naturally in mean-field transport codes and turbulent fluxes which are typically added in an ad hoc fashion. In addition, a number of further turbulent closure terms which are not commonly incorporated are identified. While it is argued that the turbulent $E\times B$![]() fluxes of heat and particles in particular are crucial closure terms to be modelled, it is left for future research to investigate which other closure terms are important and require modelling, and which ones can (remain to be) neglected. To this end, it is envisaged to evaluate these terms using reference data from (fluid) turbulence codes.
fluxes of heat and particles in particular are crucial closure terms to be modelled, it is left for future research to investigate which other closure terms are important and require modelling, and which ones can (remain to be) neglected. To this end, it is envisaged to evaluate these terms using reference data from (fluid) turbulence codes.
Following the ansatz developed in earlier work (Bufferand et al. Reference Bufferand, Ciraolo, Ghendrih, Marandet, Bucalossi, Colin, Fedorczak, Galassi, Gunn and Leybros2016; Baschetti et al. Reference Baschetti, Bufferand, Ciraolo, Fedorczak, Ghendrih, Serre and Tamain2018a,Reference Baschetti, Bufferand, Ciraolo and Ghendrihb, Reference Baschetti, Bufferand, Ciraolo, Fedorczak, Ghendrih, Tamain and Serre2019, Reference Baschetti, Bufferand, Ciraolo, Ghendrih, Serre and Tamain2021; Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2020, Reference Coosemans, Dekeyser and Baelmans2021a,Reference Coosemans, Dekeyser and Baelmansb, Reference Coosemans, Dekeyser and Baelmans2022; Coosemans Reference Coosemans2022) that these turbulent closure terms and the turbulent $E\times B$![]() fluxes especially can be modelled to a satisfactory accuracy from the turbulent kinetic energy, energy equations are developed for the plasma edge. An energy theorem has been developed in which the transfer channels between perpendicular and parallel, mean-field and turbulent (ion) kinetic energy, thermal energy of ions and electrons and mean-field and turbulent magnetic energy (in the parallel magnetic vector potential) are identified. Transport terms in space for these different energy forms are likewise derived. These equations are in line with Scott (Reference Scott2003), but improve on the rigour of the averaging operators and retain a number of additional effects.
fluxes especially can be modelled to a satisfactory accuracy from the turbulent kinetic energy, energy equations are developed for the plasma edge. An energy theorem has been developed in which the transfer channels between perpendicular and parallel, mean-field and turbulent (ion) kinetic energy, thermal energy of ions and electrons and mean-field and turbulent magnetic energy (in the parallel magnetic vector potential) are identified. Transport terms in space for these different energy forms are likewise derived. These equations are in line with Scott (Reference Scott2003), but improve on the rigour of the averaging operators and retain a number of additional effects.
This analysis has taken another step forward by deriving equations for the kinetic energy in the $E\times B$![]() velocity fluctuations specifically. That is, the perpendicular kinetic energy is decomposed into contributions due to the $E\times B$
velocity fluctuations specifically. That is, the perpendicular kinetic energy is decomposed into contributions due to the $E\times B$![]() velocity, the ion diamagnetic velocity and a mix between the previous two. This analysis shows that the commonly considered interchange and DW transfer channels exchange energy with the $E\times B$
velocity, the ion diamagnetic velocity and a mix between the previous two. This analysis shows that the commonly considered interchange and DW transfer channels exchange energy with the $E\times B$![]() kinetic energy specifically. A specific form of the RSs is also found to act on this energy specifically. Next to these well-known effects, a number of other closure terms are found as well. Earlier work (Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2020, Reference Coosemans, Dekeyser and Baelmans2021b, Reference Coosemans, Dekeyser and Baelmans2022; Coosemans Reference Coosemans2022) has found a term transporting $k_{E}$
kinetic energy specifically. A specific form of the RSs is also found to act on this energy specifically. Next to these well-known effects, a number of other closure terms are found as well. Earlier work (Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2020, Reference Coosemans, Dekeyser and Baelmans2021b, Reference Coosemans, Dekeyser and Baelmans2022; Coosemans Reference Coosemans2022) has found a term transporting $k_{E}$![]() in the parallel direction by the effect of parallel current and potential fluctuations to be a major player. For the other terms, further research will again have to establish which ones are to be retained. It may be particularly enlightening to apply the dominant balance analysis framework as presented by Callaham et al. (Reference Callaham, Koch, Brunton, Kutz and Brunton2021) to automatically identify regions in space or time where certain subsets of terms dominate the dynamics, and possibly to find scaling laws delimiting these regions.
in the parallel direction by the effect of parallel current and potential fluctuations to be a major player. For the other terms, further research will again have to establish which ones are to be retained. It may be particularly enlightening to apply the dominant balance analysis framework as presented by Callaham et al. (Reference Callaham, Koch, Brunton, Kutz and Brunton2021) to automatically identify regions in space or time where certain subsets of terms dominate the dynamics, and possibly to find scaling laws delimiting these regions.
While these theoretical derivations are interesting in their own right since they provide insight in the sources, sinks and transport effects in plasma edge turbulence, the goal is to develop a practical model for the average turbulent transport based on this physics. A preliminary model incorporating a subset of this dynamics has already been presented by Dekeyser et al. (Reference Dekeyser, Coosemans, Carli and Baelmans2022). Most notably, it uses a generally valid relation for the interchange term (Coosemans et al. Reference Coosemans, Dekeyser and Baelmans2021b, Reference Coosemans, Dekeyser and Baelmans2022) of $k_{E}$![]() , which automatically introduces a ballooning of the turbulent transport coefficients. The ‘anomalous’ transport of $k_{E}$
, which automatically introduces a ballooning of the turbulent transport coefficients. The ‘anomalous’ transport of $k_{E}$![]() through parallel current fluctuations leads to spreading of the turbulence in the parallel direction and removes the turbulence to the target plates in the SOL. The analytical set of mean-field equations presented here will clearly guide the further development of this $k_{\perp }$
through parallel current fluctuations leads to spreading of the turbulence in the parallel direction and removes the turbulence to the target plates in the SOL. The analytical set of mean-field equations presented here will clearly guide the further development of this $k_{\perp }$![]() transport model. In this way, this work represents a crucial stepping stone for the development of self-consistent turbulent transport models for mean-field simulations.
transport model. In this way, this work represents a crucial stepping stone for the development of self-consistent turbulent transport models for mean-field simulations.
Acknowledgements
Editor Peter Catto thanks the referees for their advice in evaluating this article.
Funding
R. Coosemans has been funded by a strategic basic research grant of the Research Foundation Flanders (FWO), file number 48697. This work has been carried out within the framework of the EUROfusion Consortium, partially funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No 101052200 – EUROfusion). The Swiss contribution to this work has been funded by the Swiss State Secretariat for Education, Research and Innovation (SERI). Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union, the European Commission or SERI. Neither the European Union nor the European Commission nor SERI can be held responsible for them.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Enstrophy equations
A.1. Vorticity equations
The charge balance equation (2.20) is commonly rewritten as a transport equation for a quantity that approximates the parallel component of the vorticity, which we will call the pseudo-vorticity $W$![]() . This is usually the form of the charge balance equation that is solved in plasma edge turbulence codes. In this paper, we follow the definition of the pseudo-vorticity used in the TOKAM3X code (Tamain et al. Reference Tamain, Bufferand, Ciraolo, Colin, Galassi, Ghendrih, Schwander and Serre2016)
. This is usually the form of the charge balance equation that is solved in plasma edge turbulence codes. In this paper, we follow the definition of the pseudo-vorticity used in the TOKAM3X code (Tamain et al. Reference Tamain, Bufferand, Ciraolo, Colin, Galassi, Ghendrih, Schwander and Serre2016)
In this equation, we at once defined the $E\times B$![]() and the (ion) diamagnetic pseudo-vorticities $W_E$
and the (ion) diamagnetic pseudo-vorticities $W_E$![]() and $W_*$
and $W_*$![]() . Through algebraic manipulation, the original charge balance equation can then be written as (Coosemans Reference Coosemans2022)
. Through algebraic manipulation, the original charge balance equation can then be written as (Coosemans Reference Coosemans2022)

An equation for the $E\times B$![]() -only pseudo-vorticity can likewise be obtained as (Coosemans Reference Coosemans2022)
-only pseudo-vorticity can likewise be obtained as (Coosemans Reference Coosemans2022)


A.2. Total enstrophy equations
In this work, we define the total, mean-field and turbulent (pseudo-)enstrophies based on pseudo-vorticity that we just introduced
To analytically derive transport equations for the enstrophy, we follow a procedure similar to the work Tran et al. (Reference Tran, Kim, Jhang and Kim2019), but allow independent density fluctuations, and we split the resulting equation into mean flow and turbulent contributions. An equation for the total enstrophy is readily be obtained by multiplying (pseudo-)vorticity equation (A2) with the (pseudo-)vorticity $W$![]()
A mean-field enstrophy equation is then obtained by taking the product of $\tilde {W}$![]() and the average of the vorticity equation (A2)
and the average of the vorticity equation (A2)

The difference between the average of (A7) and (A8) then allows us to write the turbulent enstrophy equation as

A.3. The $E\times B$ -only enstrophy equations
-only enstrophy equations
In complete analogy to the previous section, we define the $E\times B$![]() -only (pseudo-)enstrophies as
-only (pseudo-)enstrophies as

and derive equations for them based on (A2)