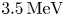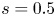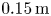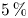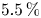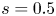1 Introduction
Unlike toroidal confinement concepts with an explicit direction of continuous symmetry, stellarators need to be optimized to ensure that collisionless drift-orbits are confined. One way to achieve such confinement is to optimize the magnetic field to be quasi-symmetric. In a quasi-symmetric field, the magnetic field strength $B$![]() is constant with respect to a linear combination of the Boozer angles – special coordinates in which the particle dynamics only explicitly depend on the magnitude of $B$
is constant with respect to a linear combination of the Boozer angles – special coordinates in which the particle dynamics only explicitly depend on the magnitude of $B$![]() instead of the full magnetic vector field $\boldsymbol {B}$
instead of the full magnetic vector field $\boldsymbol {B}$![]() . As a result, the particle orbits behave as if the field had an exact symmetry (Boozer Reference Boozer1983). Depending on the direction of symmetry in $B$
. As a result, the particle orbits behave as if the field had an exact symmetry (Boozer Reference Boozer1983). Depending on the direction of symmetry in $B$![]() , the contours of $B$
, the contours of $B$![]() will close either toroidally, helically or poloidally, and the field is said to be quasi-axisymmetric (QA), quasi-helically symmetric (QH) or quasi-poloidally symmetric (QP). Apart from true axisymmetry, exact quasi-symmetry is believed to be impossible to achieve in the entire toroidal volume (Garren & Boozer Reference Garren and Boozer1991), but it is possible to approximate quasi-symmetry to high accuracy (Nührenberg & Zille Reference Nührenberg and Zille1988).
will close either toroidally, helically or poloidally, and the field is said to be quasi-axisymmetric (QA), quasi-helically symmetric (QH) or quasi-poloidally symmetric (QP). Apart from true axisymmetry, exact quasi-symmetry is believed to be impossible to achieve in the entire toroidal volume (Garren & Boozer Reference Garren and Boozer1991), but it is possible to approximate quasi-symmetry to high accuracy (Nührenberg & Zille Reference Nührenberg and Zille1988).
Recent developments in stellarator optimization have led to a variety of new magnetic field configurations with record low quasi-symmetry error (Landreman & Paul Reference Landreman and Paul2022). However, for these improvements to be of practical relevance, it is necessary to produce the configurations with discrete electromagnetic coils. The goal of this paper is to demonstrate that it is indeed possible to find coils for several recent QH configurations.
In the conventional approach to stellarator design, a magnetic configuration is first optimized for confinement and other properties (stage I optimization), and a second optimization (stage II optimization) is used to find coils that reproduce this optimized configuration to sufficient accuracy (Merkel Reference Merkel1987; Strickler, Berry & Hirshman Reference Strickler, Berry and Hirshman2002). Coils can be optimized either through current–potential methods, where currents are optimized on a specified winding-surface (Merkel Reference Merkel1987; Landreman Reference Landreman2017) or using filamentary coils, where the optimization is done directly on parameters describing the coil shapes and currents (Zhu et al. Reference Zhu, Hudson, Song and Wan2017).
The latter is the approach taken here. Specifically, we search for optimized coils for the precise quasi-helical vacuum configuration found by Landreman & Paul (Reference Landreman and Paul2022), a similar 4-field-period QH configuration with $5\,\%$![]() volume-averaged plasma $\beta$
volume-averaged plasma $\beta$![]() (Landreman, Buller & Drevlak Reference Landreman, Buller and Drevlak2022) and a similar $5\,\%$
(Landreman, Buller & Drevlak Reference Landreman, Buller and Drevlak2022) and a similar $5\,\%$![]() $\beta$
$\beta$![]() QH configuration also optimized for Mercier stability. Here, $\beta$
QH configuration also optimized for Mercier stability. Here, $\beta$![]() is the ratio of plasma thermal energy density to magnetic energy density.
is the ratio of plasma thermal energy density to magnetic energy density.
The coils presented here are among the first to achieve precise quasi-helical symmetry. While coils for QH configurations have been designed and even built in the past (Anderson et al. Reference Anderson, Almagri, Anderson, Matthews, Talmadge and Shohet1995; Bader et al. Reference Bader, Faber, Schmitt, Anderson, Drevlak, Duff, Frerichs, Hegna, Kruger and Landreman2020), these configurations had significantly higher quasi-symmetry error. Previously, coils producing several precisely quasi-axisymmetric fields were presented by Wechsung et al. (Reference Wechsung, Landreman, Giuliani, Cerfon and Stadler2022b). Coils for quasi-helical symmetry were recently presented briefly by Roberg-Clark et al. (Reference Roberg-Clark, Plunk, Xanthopoulos, Nührenberg, Henneberg and Smith2023), although the field produced by these coils was not analysed in detail.
Much of the difficulty in coil optimization lies in the trade-off between accurately reproducing the fields and coil complexity. Coil complexity can be a major factor in the construction cost of a stellarator (Strykowsky et al. Reference Strykowsky, Brown, Chrzanowski, Cole, Heitzenroeder, Neilson, Rej and Viola2012; Klinger et al. Reference Klinger, Baylard, Beidler, Boscary, Bosch, Dinklage, Hartmann, Helander, Maßberg and Peacock2013). Coils also require shielding from high plasma temperatures and neutron bombardment, so a minimum distance from the plasma surface must be maintained. There should also be gaps between coils large enough to allow for access to the plasma by diagnostics and for maintenance, and to accommodate strain from the strong magnetic forces at work. Coil optimization must account for these different competing objectives for coils to be practical.
A downside of doing the coil optimization separately from the optimization of the magnetic configuration is that different configurations with similar performance may be easier to reproduce accurately with simple coils. For this reason, coil optimization is sometimes incorporated into the optimization of the plasma shape (Pomphrey et al. Reference Pomphrey, Berry, Boozer, Brooks, Hatcher, Hirshman, Ku, Miner, Mynick and Reiersen2001; Giuliani et al. Reference Giuliani, Wechsung, Cerfon, Landreman and Stadler2023; Jorge et al. Reference Jorge, Goodman, Landreman, Rodrigues and Wechsung2023). However, this comes with the downside of needing to optimize a more complicated objective function with more parameters. An alternative approach may be to instead penalize aspects of the magnetic configuration that lead to more complicated coils, such as scale-lengths in the magnetic field (Kappel, Landreman & Malhotra Reference Kappel, Landreman and Malhotra2023).
Small error tolerances are another driver of costs in stellarator construction. The National Compact Stellarator eXperiment (NCSX) was cancelled due to the escalating costs associated with the precision required for the coils (Strykowsky et al. Reference Strykowsky, Brown, Chrzanowski, Cole, Heitzenroeder, Neilson, Rej and Viola2012). Hence, it is important to investigate the robustness of coils with respect to errors.
The rest of the paper is structured as follows. In § 2.1, we present the QH configurations in more detail and describe some of their properties. In § 2.2, we outline the method of optimization for finding accurate and simple coils. In § 2.3, we introduce a measurement of error tolerance and compute it for our coils. In § 3, we show a specific set of coils found for the vacuum case and give several metrics of comparison with the original QH configuration. We then present coils for two finite-$\beta$![]() QH configurations and evaluate their performance. Finally, we summarize our results in § 4.
QH configurations and evaluate their performance. Finally, we summarize our results in § 4.
Our coils and optimization scripts are available from Zenodo at https://doi.org/10.5281/zenodo.10211349, see Wiedman, Buller & Landreman (Reference Wiedman, Buller and Landreman2023).
2 Method
2.1 Stellarator configurations
The three QH stellarator configurations we will consider are all stellarator symmetric, with $n_{\text {fp}} = 4$![]() field periods. The configurations all have a volume-averaged magnetic field strength $B$
field periods. The configurations all have a volume-averaged magnetic field strength $B$![]() of $5.86\,\mathrm {T}$
of $5.86\,\mathrm {T}$![]() and a minor radius $a=1.7\,\mathrm {m}$
and a minor radius $a=1.7\,\mathrm {m}$![]() to match the ARIES-CS reactor design (Najmabadi et al. Reference Najmabadi, Raffray, Abdel-Khalik, Bromberg, Crosatti, El-Guebaly, Garabedian, Grossman, Henderson and Ibrahim2008). As we only consider modular coils, scaling to the same minor radius roughly ensures that the coils we consider are of comparable sizes. Scaling both minor radius and magnetic field to reactor-relevant values is done for the sake of comparing the confinement of fusion-born alpha particles (Bader et al. Reference Bader, Anderson, Drevlak, Faber, Hegna, Henneberg, Landreman, Schmitt, Suzuki and Ware2021; Landreman & Paul Reference Landreman and Paul2022).
to match the ARIES-CS reactor design (Najmabadi et al. Reference Najmabadi, Raffray, Abdel-Khalik, Bromberg, Crosatti, El-Guebaly, Garabedian, Grossman, Henderson and Ibrahim2008). As we only consider modular coils, scaling to the same minor radius roughly ensures that the coils we consider are of comparable sizes. Scaling both minor radius and magnetic field to reactor-relevant values is done for the sake of comparing the confinement of fusion-born alpha particles (Bader et al. Reference Bader, Anderson, Drevlak, Faber, Hegna, Henneberg, Landreman, Schmitt, Suzuki and Ware2021; Landreman & Paul Reference Landreman and Paul2022).
The precise QH configuration from Landreman & Paul (Reference Landreman and Paul2022) has an aspect ratio $A = 8.0$![]() and mean rotational transform $\iota = 1.24$
and mean rotational transform $\iota = 1.24$![]() , is a vacuum field, and is optimized purely for low quasi-symmetry error and the achieved aspect ratio, without taking magneto-hydrodynamic (MHD) stability into account.
, is a vacuum field, and is optimized purely for low quasi-symmetry error and the achieved aspect ratio, without taking magneto-hydrodynamic (MHD) stability into account.
The second configuration, from Landreman et al. (Reference Landreman, Buller and Drevlak2022), has $A=6.5$![]() and volume-averaged $\beta =5\,\%$
and volume-averaged $\beta =5\,\%$![]() , and was optimized to have self-consistent bootstrap current and a rotational transform profile $\iota$
, and was optimized to have self-consistent bootstrap current and a rotational transform profile $\iota$![]() that avoids crossing $\iota =1$
that avoids crossing $\iota =1$![]() , but is otherwise not optimized for MHD stability.
, but is otherwise not optimized for MHD stability.
The third configuration was generated using the same optimization method as Landreman et al. (Reference Landreman, Buller and Drevlak2022), but with the addition of a Mercier stability term to the objective function, resulting in Mercier stability throughout the plasma. It is otherwise similar to the second configuration. This configuration has not appeared in a previous publication.
2.2 Computational tools and optimization objective
To perform an optimization, coils must be represented mathematically. Using the SIMSOPT framework (Landreman et al. Reference Landreman, Medasani, Wechsung, Giuliani, Jorge and Zhu2021), we describe coils as curves in space determined by a Fourier series for each of the three Cartesian coordinates of the coils. We neglect the volume of the coils and instead represent them as current-carrying filaments. This is an often used approximation for optimizing stellarator coils, but it neglects corrections due to the finite-build of the coils. Such corrections are expected to be important when the width of the coils are comparable to the coil–plasma distance (McGreivy, Hudson & Zhu Reference McGreivy, Hudson and Zhu2021). Visual inspection of a CAD model of Wendelstein 7-X suggests that this criterion may only be weakly satisfied in actual stellarators (Pedersen et al. Reference Pedersen, Otte, Lazerson, Helander, Bozhenkov, Biedermann, Klinger, Wolf and Bosch2016), but including these effects is outside the scope of the current study. Filamentary coils are also insufficient to account for the magnetic forces on the coils, where information about the cross-sections of the coils must be supplemented (Hurwitz, Landreman & Antonsen Reference Hurwitz, Landreman and Antonsen2023; Landreman, Hurwitz & Antonsen Reference Landreman, Hurwitz and Antonsen2023).
For our filamentary coils, each Cartesian component of the curve is represented as

where $\varphi$![]() is an angle-like variable parametrizing the coil and $N$
is an angle-like variable parametrizing the coil and $N$![]() is the number of Fourier modes used in the representation.
is the number of Fourier modes used in the representation.
We optimize the coils with the limited-memory BFGS algorithm from the scipy library (Virtanen et al. Reference Virtanen, Gommers, Oliphant, Haberland, Reddy, Cournapeau, Burovski, Peterson, Weckesser and Bright2020). SIMSOPT uses Python for front-end programming and C++ for back-end calculations, resulting in a fast and user-friendly environment. This optimization algorithm is local rather than global, so it is possible that better coils may exist.
Optimization of the coils is performed by minimizing the objective function

where the first term corresponds to the square of the flux of the magnetic field created by the coils through the target plasma surface. Here, $\boldsymbol {B}$![]() is the magnetic field created by the coils and $\boldsymbol {\hat {n}}$
is the magnetic field created by the coils and $\boldsymbol {\hat {n}}$![]() is the unit vector normal to the target surface. The $f_i$
is the unit vector normal to the target surface. The $f_i$![]() terms are related to various aspect of the coils and are defined as follows:
terms are related to various aspect of the coils and are defined as follows:
where $L_i$![]() is the length of each coil and $L_0$
is the length of each coil and $L_0$![]() is a target coil length;
is a target coil length;
where $\min {d_{i,j}}$![]() is the closest distance between any point on coil $i$
is the closest distance between any point on coil $i$![]() and any point on coil $j$
and any point on coil $j$![]() with a threshold value of $d_{\mathrm {cc}, 0}$
with a threshold value of $d_{\mathrm {cc}, 0}$![]() below which the penalty applies. This penalizes coils that are too close to one another;
below which the penalty applies. This penalizes coils that are too close to one another;
where $\min {d_{\mathrm {cs}, i}}$![]() is the minimum distance between any point on coil $i$
is the minimum distance between any point on coil $i$![]() and the boundary magnetic surface, and $d_{\mathrm {cs}, 0}$
and the boundary magnetic surface, and $d_{\mathrm {cs}, 0}$![]() is a threshold distance. This term penalizes coils that are placed within $d_{\mathrm {cs}, 0}$
is a threshold distance. This term penalizes coils that are placed within $d_{\mathrm {cs}, 0}$![]() of the plasma surface;
of the plasma surface;
where $\kappa _i$![]() is the curvature on each coil and $\kappa _0$
is the curvature on each coil and $\kappa _0$![]() is the threshold curvature above which the penalty applies, penalizing coils with high maximum curvature. The integral is over $l$
is the threshold curvature above which the penalty applies, penalizing coils with high maximum curvature. The integral is over $l$![]() , the arclength along the coil;
, the arclength along the coil;

where $\kappa _i(l)$![]() is the curvature along the length of coil $i$
is the curvature along the length of coil $i$![]() and $\mathrm {MSC}_0$
and $\mathrm {MSC}_0$![]() is the threshold value, discouraging the optimizer from considering coils with high mean-squared curvature (MSC);
is the threshold value, discouraging the optimizer from considering coils with high mean-squared curvature (MSC);

where we use Gauss’ linking number integral formula,
where $c_i$![]() is the first curve, $c_j$
is the first curve, $c_j$![]() is the second curve, and $\boldsymbol {r}_i$
is the second curve, and $\boldsymbol {r}_i$![]() and $\boldsymbol {r}_j$
and $\boldsymbol {r}_j$![]() are the associated position vectors (Ricca & Nipoti Reference Ricca and Nipoti2011). This prevents interlocking coils from being considered. Since the numerical implementation of the above integral will not be exactly zero, we use a quadratic penalty in $f_6$
are the associated position vectors (Ricca & Nipoti Reference Ricca and Nipoti2011). This prevents interlocking coils from being considered. Since the numerical implementation of the above integral will not be exactly zero, we use a quadratic penalty in $f_6$![]() to suppress small values. The threshold value $0.1$
to suppress small values. The threshold value $0.1$![]() is taken to be much larger than the numerical errors and much smaller than $1$
is taken to be much larger than the numerical errors and much smaller than $1$![]() . Even though the discretization error is small, typically below 0.01, the total value of the objective function typically reaches $10^{-6}$
. Even though the discretization error is small, typically below 0.01, the total value of the objective function typically reaches $10^{-6}$![]() or lower. Using the ‘round’ python function has the same effect. Suppressing the errors in the linking number thus drastically improves the performance of the optimization.
or lower. Using the ‘round’ python function has the same effect. Suppressing the errors in the linking number thus drastically improves the performance of the optimization.
We use a normalized form of the error in the calculated magnetic field
as our measurement of how successfully the coils reproduce the target surface, where $\langle A \rangle$![]() is the flux surface average of $A$
is the flux surface average of $A$![]() .
.
Another measure of success is whether energetic particle trajectories remain confined. To this end, the guiding-centre tracing code SIMPLE (Albert, Kasilov & Kernbichler Reference Albert, Kasilov and Kernbichler2020a,Reference Albert, Kasilov and Kernbichlerb) is used to calculate the loss fraction of high energy $\alpha$![]() particles. For all our configurations, we use SIMPLE to trace 5000 alpha particles with energies of $3.5\,\mathrm {MeV}$
particles. For all our configurations, we use SIMPLE to trace 5000 alpha particles with energies of $3.5\,\mathrm {MeV}$![]() for $0.2$
for $0.2$![]() seconds, typical of the slowing-down time in a reactor. Particles are launched in a uniformly random direction at the flux surfaces with normalized toroidal flux $s = 0.3$
seconds, typical of the slowing-down time in a reactor. Particles are launched in a uniformly random direction at the flux surfaces with normalized toroidal flux $s = 0.3$![]() , $s = 0.5$
, $s = 0.5$![]() and $s=0.7$
and $s=0.7$![]() , and are considered lost when they cross the $s=1.0$
, and are considered lost when they cross the $s=1.0$![]() surface, corresponding to the last closed flux surface. SIMPLE traces the collisionless guiding-centre orbits, so the energy of the alpha particles remains constant. To compare fast-particle confinement across devices, we scale all configurations to have the same minor radius and volume-averaged magnetic field.
surface, corresponding to the last closed flux surface. SIMPLE traces the collisionless guiding-centre orbits, so the energy of the alpha particles remains constant. To compare fast-particle confinement across devices, we scale all configurations to have the same minor radius and volume-averaged magnetic field.
2.3 Error tolerance
Error tolerance tests are performed through the use of the CurvePerturbed class in SIMSOPT. A set of coils has their Cartesian coordinates perturbed through a Gaussian process that depends on the length scale $\ell$![]() , a measurement of the smoothness of the random function generated and a parameter $\sigma$
, a measurement of the smoothness of the random function generated and a parameter $\sigma$![]() that scales the standard deviation of the perturbations. Following Wechsung et al. (Reference Wechsung, Giuliani, Landreman, Cerfon and Stadler2022a), $\ell$
that scales the standard deviation of the perturbations. Following Wechsung et al. (Reference Wechsung, Giuliani, Landreman, Cerfon and Stadler2022a), $\ell$![]() is kept at a constant value of $0.4{\rm \pi}$
is kept at a constant value of $0.4{\rm \pi}$![]() , while $\sigma$
, while $\sigma$![]() varies between $0.01\,\mathrm {m}$
varies between $0.01\,\mathrm {m}$![]() and $0.1\,\mathrm {m}$
and $0.1\,\mathrm {m}$![]() . The Gaussian process model for the perturbation $X(\varphi )$
. The Gaussian process model for the perturbation $X(\varphi )$![]() is described by the radial basis function kernel
is described by the radial basis function kernel

where $\varphi$![]() parametrizes the curve, and shifting by all integers $j$
parametrizes the curve, and shifting by all integers $j$![]() times $2{\rm \pi}$
times $2{\rm \pi}$![]() makes the perturbation periodic with period $2{\rm \pi}$
makes the perturbation periodic with period $2{\rm \pi}$![]() . (Note that the actual coil parametrization in SIMSOPT goes from 0 to 1). The series can be truncated at a low number of integers due to the fall off of the exponential function. This exact kernel was previously used by Wechsung et al. (Reference Wechsung, Giuliani, Landreman, Cerfon and Stadler2022a) to describe coil errors. At $\ell =0.4{\rm \pi}$
. (Note that the actual coil parametrization in SIMSOPT goes from 0 to 1). The series can be truncated at a low number of integers due to the fall off of the exponential function. This exact kernel was previously used by Wechsung et al. (Reference Wechsung, Giuliani, Landreman, Cerfon and Stadler2022a) to describe coil errors. At $\ell =0.4{\rm \pi}$![]() , $\sigma = 0.01\,\mathrm {m}$
, $\sigma = 0.01\,\mathrm {m}$![]() and $\sigma = 0.1\,\mathrm {m}$
and $\sigma = 0.1\,\mathrm {m}$![]() correspond to coil errors with with average amplitudes of approximately $3\,\mathrm {cm}$
correspond to coil errors with with average amplitudes of approximately $3\,\mathrm {cm}$![]() and $30\,\mathrm {cm}$
and $30\,\mathrm {cm}$![]() , respectively.
, respectively.
After the perturbations are applied to our coils, we recalculate the metrics used to evaluate the quality of the coils.
3 Results
3.1 Landreman–Paul precise QH
We first optimized coils for the precise QH vacuum configuration presented in § 2.1 using the method outlined in § 2.2, trying various weights for the objective terms $f_i$![]() in (2.2). The optimizations were performed independently from one another, starting from a set of equally spaced, circular coils with a major radius of approximately $13\,\mathrm {m}$
in (2.2). The optimizations were performed independently from one another, starting from a set of equally spaced, circular coils with a major radius of approximately $13\,\mathrm {m}$![]() and a minor radius of $6.5\,\mathrm {m}$
and a minor radius of $6.5\,\mathrm {m}$![]() . Weights are constant for each optimization. The target curvature is changed between each run to induce meaningful variations in the accuracy of the coils, while still remaining below or comparable to the curvature of NCSX and HSX. The most successful set of coils is shown in figure 1. This set of coils was obtained using weights outlined in table 1.
. Weights are constant for each optimization. The target curvature is changed between each run to induce meaningful variations in the accuracy of the coils, while still remaining below or comparable to the curvature of NCSX and HSX. The most successful set of coils is shown in figure 1. This set of coils was obtained using weights outlined in table 1.

Figure 1. Target plasma surface of the Landreman–Paul precise QH configuration with the associated optimized coil set. The colour scale shows the error in the $B$![]() field from the target surface as quantified by $|\boldsymbol {B} \boldsymbol {\cdot } \boldsymbol {\hat {n}}|/B$
field from the target surface as quantified by $|\boldsymbol {B} \boldsymbol {\cdot } \boldsymbol {\hat {n}}|/B$![]() . The colour of each coil indicates the index, with blue being coil 1, turquoise being coil 2, green being coil 3, orange being coil 4 and red being coil 5.
. The colour of each coil indicates the index, with blue being coil 1, turquoise being coil 2, green being coil 3, orange being coil 4 and red being coil 5.
Table 1. Weights placed on terms in objective function as described in (2.2), as well as the target values and the achieved values averaged across the set of coils, for the coil set described in § 3.1. The National Compact Stellarator eXperiment (NCSX) (Williamson et al. Reference Williamson, Brooks, Brown, Chrzanowski, Cole, Fan, Freudenberg, Fogarty, Hargrove and Heitzenroeder2005) and the Helically Symmetric eXperiment (HSX) (Anderson et al. Reference Anderson, Almagri, Anderson, Matthews, Talmadge and Shohet1995) metrics are shown as a comparison, scaled up to the plasma minor radius of ARIES-CS (Najmabadi et al. Reference Najmabadi, Raffray, Abdel-Khalik, Bromberg, Crosatti, El-Guebaly, Garabedian, Grossman, Henderson and Ibrahim2008). Here, $L$![]() is the average coil length (averaged across unique coils), $\kappa$
is the average coil length (averaged across unique coils), $\kappa$![]() is the maximum curvature and MSC is the mean squared curvature. The target of $\kappa$
is the maximum curvature and MSC is the mean squared curvature. The target of $\kappa$![]() being greater than the achieved value means the maximum curvature had no effect on the cost function at the end; however, the minimizer was able to move through different values while searching for different minima and the results were different than they would be for different target values.
being greater than the achieved value means the maximum curvature had no effect on the cost function at the end; however, the minimizer was able to move through different values while searching for different minima and the results were different than they would be for different target values.

The set contains five coils per half-period, 40 coils in total. This number of coils was chosen for the higher accuracy it was able to provide over four-coil configurations, while still being able to maintain the desired coil to coil separation, which is much more difficult with a six-coil configuration. Metrics for the five individual coils are presented in table 2. The coil lengths average to 35.56 m. They maintain a distance of 1.09 m between one another at minimum, and a minimum distance of 1.62 m to the boundary surface. Each coil has a maximum curvature between 0.6 $\mathrm {m}^{-1}$![]() and 0.8 $\mathrm {m}^{-1}$
and 0.8 $\mathrm {m}^{-1}$![]() , with coils having a range of MSC between $0.062\,\mathrm {m}^{-1}$
, with coils having a range of MSC between $0.062\,\mathrm {m}^{-1}$![]() and $0.079\,\mathrm {m}^{-1}$
and $0.079\,\mathrm {m}^{-1}$![]() , averaging at 0.069 $\mathrm {m}^{-1}$
, averaging at 0.069 $\mathrm {m}^{-1}$![]() . The target coil length, coil to coil distance, coil to surface distance and curvature were all achieved or surpassed, while the mean squared curvature was slightly higher than the target. These values are all comparable to those of NCSX and HSX when scaled up to the same minor radius, with the curvature and MSC metrics of our coil set being lower. Since scaling the size of a configuration does not affect the accuracy of the normal field error for vacuum fields, we are free to rescale our configurations arbitrarily as long as we also scale the thresholds in curvature, plasma–coil spacing and so on; scaling to reactor size is convenient since it allows us to set a lower bound for coil–plasma distance based on the ${\sim }1.5\,\mathrm {m}$
. The target coil length, coil to coil distance, coil to surface distance and curvature were all achieved or surpassed, while the mean squared curvature was slightly higher than the target. These values are all comparable to those of NCSX and HSX when scaled up to the same minor radius, with the curvature and MSC metrics of our coil set being lower. Since scaling the size of a configuration does not affect the accuracy of the normal field error for vacuum fields, we are free to rescale our configurations arbitrarily as long as we also scale the thresholds in curvature, plasma–coil spacing and so on; scaling to reactor size is convenient since it allows us to set a lower bound for coil–plasma distance based on the ${\sim }1.5\,\mathrm {m}$![]() required thickness of blanket and neutron shielding (Najmabadi et al. Reference Najmabadi, Raffray, Abdel-Khalik, Bromberg, Crosatti, El-Guebaly, Garabedian, Grossman, Henderson and Ibrahim2008).
required thickness of blanket and neutron shielding (Najmabadi et al. Reference Najmabadi, Raffray, Abdel-Khalik, Bromberg, Crosatti, El-Guebaly, Garabedian, Grossman, Henderson and Ibrahim2008).
Table 2. Length and curvature metrics of each unique coil in the coil set presented in § 3.1. There are five coils in the set, resulting in 40 total coils due to 4-field-period symmetry and stellarator symmetry. See table 1 for definitions. See figure 1 for a visualization of the coils.

The normalized flux surface average of the $B$![]() field from the coils normal to the target surface (2.10) is $6 \times 10^{-4}$
field from the coils normal to the target surface (2.10) is $6 \times 10^{-4}$![]() while the maximum $\boldsymbol {B}_{\text {coils}} \boldsymbol {\cdot } \boldsymbol {\hat {n}}_{\text {target}}/|\boldsymbol {B}_{\text {target}}|$
while the maximum $\boldsymbol {B}_{\text {coils}} \boldsymbol {\cdot } \boldsymbol {\hat {n}}_{\text {target}}/|\boldsymbol {B}_{\text {target}}|$![]() is $3.1\times 10^{-3}$
is $3.1\times 10^{-3}$![]() . Figure 1 shows the error in $\boldsymbol {B} \boldsymbol {\cdot } \boldsymbol {\hat {n}}$
. Figure 1 shows the error in $\boldsymbol {B} \boldsymbol {\cdot } \boldsymbol {\hat {n}}$![]() on the surface. Figures 2 and 3 both give clear indication of the high degree of accuracy with which the coils recreate the target surface. There is some coil ripple present in figure 2 which is only present in the weaker section of the magnetic field, but the quasi-helical symmetry is largely maintained by the coils. The blue curves in figure 4(a) show the root-mean-squared (r.m.s.) amplitude of the quasi-symmetry breaking modes as a function of radius for the target configuration and the configuration achieved with our coils. Figure 4(b) shows the corresponding curves for the two-term quasi-symmetry error (Helander & Simakov Reference Helander and Simakov2008), defined as
on the surface. Figures 2 and 3 both give clear indication of the high degree of accuracy with which the coils recreate the target surface. There is some coil ripple present in figure 2 which is only present in the weaker section of the magnetic field, but the quasi-helical symmetry is largely maintained by the coils. The blue curves in figure 4(a) show the root-mean-squared (r.m.s.) amplitude of the quasi-symmetry breaking modes as a function of radius for the target configuration and the configuration achieved with our coils. Figure 4(b) shows the corresponding curves for the two-term quasi-symmetry error (Helander & Simakov Reference Helander and Simakov2008), defined as

where $(M,N)=(1,-4)$![]() corresponds to the helicity of the helical symmetry of $B$
corresponds to the helicity of the helical symmetry of $B$![]() ; $2{\rm \pi} G/\mu _0$
; $2{\rm \pi} G/\mu _0$![]() and $2{\rm \pi} I/\mu _0$
and $2{\rm \pi} I/\mu _0$![]() are the poloidal current outside and toroidal current inside the flux surface, respectively. Note that the factor $4$
are the poloidal current outside and toroidal current inside the flux surface, respectively. Note that the factor $4$![]() in $N$
in $N$![]() is due to $n_{\text {fp}} = 4$
is due to $n_{\text {fp}} = 4$![]() .
.

Figure 2. Magnetic field $B$![]() on the boundary in Boozer coordinates. (a) Landreman–Paul precise QH. (b) $B$
on the boundary in Boozer coordinates. (a) Landreman–Paul precise QH. (b) $B$![]() produced by the coils presented in § 3.1.
produced by the coils presented in § 3.1.

Figure 3. Poincaré plot of the flux surfaces created by the coils presented in § 3.1, at standard toroidal angle $\phi = 0, 1/4$![]() period, $1/2$
period, $1/2$![]() period (from panel a–c). The red curve indicates the Landreman–Paul precise QH boundary targeted by the coils. The black lines depict the traced magnetic field lines within and on the boundary.
period (from panel a–c). The red curve indicates the Landreman–Paul precise QH boundary targeted by the coils. The black lines depict the traced magnetic field lines within and on the boundary.

Figure 4. Quasi-symmetry metrics for our configurations. (a) Root-mean-squared value of symmetry breaking Boozer harmonics $B_{m,n}$![]() against radius. (b) Two-term quasi-symmetry error, as defined in (3.1), against radius. Solid curves are for the target configurations, dashed curves for the configurations achieved by our coils. All configurations are scaled to match the volume-averaged $B$
against radius. (b) Two-term quasi-symmetry error, as defined in (3.1), against radius. Solid curves are for the target configurations, dashed curves for the configurations achieved by our coils. All configurations are scaled to match the volume-averaged $B$![]() and minor radius of ARIES-CS. Also included for comparison are the quasi-symmetry metrics of NCSX and HSX.
and minor radius of ARIES-CS. Also included for comparison are the quasi-symmetry metrics of NCSX and HSX.
A comparison of figure 4(b) with figure 4(a) shows that the two-term quasi-symmetry errors exhibit much larger differences between the original stage I configurations and the configurations reproduced by our coils, compared with the differences in their r.m.s. values. As shown by Rodríguez, Paul & Bhattacharjee (Reference Rodríguez, Paul and Bhattacharjee2022), the two-term form of quasi-symmetry can be written as a weighted version of the r.m.s. value of symmetry-breaking Boozer modes. Specifically, for symmetry helicity $(M,N)=(1,-4)$![]() , modes are weighted according to
, modes are weighted according to
Thus, deviations from quasi-symmetry with higher mode numbers, such as those created by modular coil ripple, are weighted more strongly in the two-term measure, which would explain the larger differences in figure 4(b). In general, different quasi-symmetry metrics can be in conflict with each other, such that improving one metric degrades the other (Rodríguez et al. Reference Rodríguez, Paul and Bhattacharjee2022). This happens when it is no longer possible to reduce the magnitude of a symmetry-breaking mode without increasing the magnitude of another mode. It is thus useful to look at other metrics that are more directly related to the relevant physics.
To evaluate the performance of our coils, we calculate how well the resulting configuration confines fast particles, using the SIMPLE simulation set-up described in § 2.2. For our coils, we find no fast-particle losses for particles launched at flux surfaces with normalized toroidal flux $s = 0.3$![]() and $s = 0.5$
and $s = 0.5$![]() , and only $1.44\,\%$
, and only $1.44\,\%$![]() losses when launched at $s=0.7$
losses when launched at $s=0.7$![]() . For reference, the original precise QH configuration loses $1.40\,\%$
. For reference, the original precise QH configuration loses $1.40\,\%$![]() of particles launched at $s=0.7$
of particles launched at $s=0.7$![]() , indicating that the field is reproduced to sufficient accuracy.
, indicating that the field is reproduced to sufficient accuracy.
To assess the error tolerance of the coil set, we generated 25 sets of coil perturbations, using the Gaussian process model described in § 2.3. The generated perturbations were scaled to different amplitudes by using ten different values for $\sigma$![]() . The perturbations were then added to our optimal set of coils, resulting in a total of 250 perturbed coil sets. Figure 5 shows a perturbed coil set, with the unperturbed coil set included for reference. The resulting flux surface averages of the $B$
. The perturbations were then added to our optimal set of coils, resulting in a total of 250 perturbed coil sets. Figure 5 shows a perturbed coil set, with the unperturbed coil set included for reference. The resulting flux surface averages of the $B$![]() field from the coils normal to the target surface are shown in figure 6, while the corresponding fast-particle losses are shown in figure 7. At $\sigma = 0.1\,\mathrm {m}$
field from the coils normal to the target surface are shown in figure 6, while the corresponding fast-particle losses are shown in figure 7. At $\sigma = 0.1\,\mathrm {m}$![]() , there is a perceptible difference in the shape of the coils, and between $0\,\%$
, there is a perceptible difference in the shape of the coils, and between $0\,\%$![]() and $5\,\%$
and $5\,\%$![]() of particles launched from a toroidal radius of $s=0.3$
of particles launched from a toroidal radius of $s=0.3$![]() are lost. Thus, there is considerable variation in particle confinement for a given $\sigma$
are lost. Thus, there is considerable variation in particle confinement for a given $\sigma$![]() .
.

Figure 5. Original coils optimized for the Landreman–Paul configuration (red) compared with a set of perturbed coils with $\sigma = 0.1\,\mathrm {m}$![]() (blue).
(blue).

Figure 6. Scatter plot of the coil perturbation magnitude $\sigma$![]() versus the normalized flux surface average of $\boldsymbol {B}\boldsymbol {\cdot } \boldsymbol {\hat {n}}$
versus the normalized flux surface average of $\boldsymbol {B}\boldsymbol {\cdot } \boldsymbol {\hat {n}}$![]() (2.10), with $\boldsymbol {B}$
(2.10), with $\boldsymbol {B}$![]() calculated from perturbed coils targeting the Landreman–Paul precise QH configuration. The line indicates the least-squares regression for the discrete values of $\sigma$
calculated from perturbed coils targeting the Landreman–Paul precise QH configuration. The line indicates the least-squares regression for the discrete values of $\sigma$![]() .
.

Figure 7. Fraction of high energy alpha particles lost when launched from different toroidal radii for the coils perturbed from the set optimized for the Landreman–Paul precise QH in figure 6. Points in the plot are offset slightly in the $x$![]() direction for readability.
direction for readability.
To better understand the large spread in fast-particle losses, we plot the losses for particles launched from $s=0.3$![]() against both the error in the target field, the flux surface average (figure 8) and the quasi-symmetry error (figure 9). In figure 9, we sum the quasi-symmetry error defined by (3.1) for each of the flux surfaces $s = \{0, 0.1, \ldots, 1.0\}$
against both the error in the target field, the flux surface average (figure 8) and the quasi-symmetry error (figure 9). In figure 9, we sum the quasi-symmetry error defined by (3.1) for each of the flux surfaces $s = \{0, 0.1, \ldots, 1.0\}$![]() , and thus obtain a scalar measure of the quasi-symmetry error in the entire plasma volume from axis to edge.
, and thus obtain a scalar measure of the quasi-symmetry error in the entire plasma volume from axis to edge.

Figure 8. Scatter plot and two-dimensional (2-D) histogram of the loss fraction of high energy alpha particles launched at $s=0.3$![]() , against the flux surface average $\boldsymbol {B} \boldsymbol {\cdot } \boldsymbol {\hat {n}}$
, against the flux surface average $\boldsymbol {B} \boldsymbol {\cdot } \boldsymbol {\hat {n}}$![]() , for the coils perturbed from the set optimized for the Landreman–Paul precise QH configuration.
, for the coils perturbed from the set optimized for the Landreman–Paul precise QH configuration.

Figure 9. Scatter plot and 2-D histogram of the loss fraction of high energy alpha particles launched at $s=0.3$![]() , against different values of quasi-symmetry error for the coils perturbed from the set optimized for the Landreman–Paul precise QH configuration. The quasi-symmetry error is defined in (3.1) and summed over the $s=\{0, 0.1,\ldots 0.9, 1.0\}$
, against different values of quasi-symmetry error for the coils perturbed from the set optimized for the Landreman–Paul precise QH configuration. The quasi-symmetry error is defined in (3.1) and summed over the $s=\{0, 0.1,\ldots 0.9, 1.0\}$![]() surfaces.
surfaces.
In both figures 8 and 9, poor confinement is generally only found above certain thresholds, for $\langle |\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\hat {n}}|\rangle /\langle B\rangle$![]() above $0.5\,\%$
above $0.5\,\%$![]() and quasi-symmetry error above $0.003$
and quasi-symmetry error above $0.003$![]() , but configurations with good confinement are also found well above these values. As pointed out by Rodríguez et al. (Reference Rodríguez, Paul and Bhattacharjee2022), decreasing the two-term quasi-symmetry error does not necessarily lead to an increase in performance (or even a decrease in other measures of quasi-symmetry error, as mentioned earlier). This is consistent with our findings here.
, but configurations with good confinement are also found well above these values. As pointed out by Rodríguez et al. (Reference Rodríguez, Paul and Bhattacharjee2022), decreasing the two-term quasi-symmetry error does not necessarily lead to an increase in performance (or even a decrease in other measures of quasi-symmetry error, as mentioned earlier). This is consistent with our findings here.
We attempt to further simplify the construction of the coils by optimizing with purely planar coils; however, the coil sets produced from this optimization were significantly worse than the comparative non-planar coils (see Appendix A).
3.2 Landreman–Buller–Drevlak $5\,\%$ volume-averaged $\beta$
volume-averaged $\beta$ QH
QH
We applied the optimization procedure to the $5\,\%$![]() volume-averaged $\beta$
volume-averaged $\beta$![]() QH configuration of Landreman et al. (Reference Landreman, Buller and Drevlak2022). Five coils per half-period were used again for consistency. The currents inside the plasma were accounted for using the virtual casing principle (Shafranov & Zakharov Reference Shafranov and Zakharov1972; Drevlak, Monticello & Reiman Reference Drevlak, Monticello and Reiman2005), as implemented numerically by Malhotra et al. (Reference Malhotra, Cerfon, O'Neil and Toler2019). The weights and target values in the objective function (2.2) were varied to find the values yielding the lowest value for the quantity in (2.10). The best weight and target values thus found are presented in table 3. These weights vary significantly from the weights for the vacuum case, since the metrics are mostly below the set thresholds and the objective function achieves a values significantly less than 1 (of the order of $10^-3$
QH configuration of Landreman et al. (Reference Landreman, Buller and Drevlak2022). Five coils per half-period were used again for consistency. The currents inside the plasma were accounted for using the virtual casing principle (Shafranov & Zakharov Reference Shafranov and Zakharov1972; Drevlak, Monticello & Reiman Reference Drevlak, Monticello and Reiman2005), as implemented numerically by Malhotra et al. (Reference Malhotra, Cerfon, O'Neil and Toler2019). The weights and target values in the objective function (2.2) were varied to find the values yielding the lowest value for the quantity in (2.10). The best weight and target values thus found are presented in table 3. These weights vary significantly from the weights for the vacuum case, since the metrics are mostly below the set thresholds and the objective function achieves a values significantly less than 1 (of the order of $10^-3$![]() ). Since the weights are so high in comparison to the objective value, higher orders of magnitude for the weights will not change the final optimization function too much, although it may cause some differences in the path the optimization function takes to achieve a local minimum.
). Since the weights are so high in comparison to the objective value, higher orders of magnitude for the weights will not change the final optimization function too much, although it may cause some differences in the path the optimization function takes to achieve a local minimum.
Table 3. Weights placed on terms in the objective function, as well as the target values and the achieved values averaged across the set of coils for the Landreman–Buller–Drevlak QH configuration described in § 3.2. The terms in the objective function corresponding to the weights are described in (2.2).

For the resulting coils, the normalized flux surface average of $|\boldsymbol {B} \boldsymbol {\cdot } \boldsymbol {\hat {n}}|$![]() (equation (2.10)) is $9.7 \times 10^{-4}$
(equation (2.10)) is $9.7 \times 10^{-4}$![]() . Figure 10 shows the comparison between the target surface and the surface achieved with the resulting coils, the latter of which was calculated using free-boundary VMEC (Hirshman & Whitson Reference Hirshman and Whitson1983). Figure 11 shows the magnetic field at the boundary in Boozer coordinates. The coils themselves are shown in figure 12, along with the target surface. The orange curves in figures 4(a) and 4(b) compare quasi-symmetry properties of the target configuration and the configuration achieved with the coils, displaying similar levels of relative degradation in quasi-symmetry as the Landreman–Paul precise QH.
. Figure 10 shows the comparison between the target surface and the surface achieved with the resulting coils, the latter of which was calculated using free-boundary VMEC (Hirshman & Whitson Reference Hirshman and Whitson1983). Figure 11 shows the magnetic field at the boundary in Boozer coordinates. The coils themselves are shown in figure 12, along with the target surface. The orange curves in figures 4(a) and 4(b) compare quasi-symmetry properties of the target configuration and the configuration achieved with the coils, displaying similar levels of relative degradation in quasi-symmetry as the Landreman–Paul precise QH.

Figure 10. Flux surface comparison of the Landreman–Buller–Drevlak QH $5\,\%$![]() volume-averaged $\beta$
volume-averaged $\beta$![]() configuration (red solid) and the surfaces produced by the coils (black dotted).
configuration (red solid) and the surfaces produced by the coils (black dotted).

Figure 11. Magnetic field $B$![]() on the plasma boundary in Boozer coordinates. (a) Landreman–Buller–Drevlak QH with $5\,\%$
on the plasma boundary in Boozer coordinates. (a) Landreman–Buller–Drevlak QH with $5\,\%$![]() volume-averaged $\beta$
volume-averaged $\beta$![]() . (b) $B$
. (b) $B$![]() produced by the coils presented in § 3.2.
produced by the coils presented in § 3.2.

Figure 12. Optimized coil set for the Landreman–Buller–Drevlak $5\,\%$![]() volume-averaged $\beta$
volume-averaged $\beta$![]() QH configuration (red). Coils are indexed in the same way as in figure 1.
QH configuration (red). Coils are indexed in the same way as in figure 1.
With the same fast-particle tracing simulation set-up as in § 3.1, we obtain alpha-particle loss fractions of $0.0\,\%$![]() , $2.8\,\%$
, $2.8\,\%$![]() and $10\,\%$
and $10\,\%$![]() , for particles launched at normalized toroidal flux $s=0.3$
, for particles launched at normalized toroidal flux $s=0.3$![]() , $s=0.5$
, $s=0.5$![]() and $s=0.7$
and $s=0.7$![]() , respectively. For the original (stage I) configuration, the corresponding loss fractions are $0.0\,\%$
, respectively. For the original (stage I) configuration, the corresponding loss fractions are $0.0\,\%$![]() , $0.1\,\%$
, $0.1\,\%$![]() and $4\,\%$
and $4\,\%$![]() .
.
3.3 Mercier-stable $5\,\%$ volume-averaged $\beta$
volume-averaged $\beta$ QH
QH
Finally, we optimized coils for a $5\,\%$![]() volume-averaged $\beta$
volume-averaged $\beta$![]() QH configuration that was also optimized to satisfy the Mercier criterion, again using the initial non-planar optimization method with five coils per half-period. The weights and target values of the optimization yielding the best coils are presented in table 4. The boundary of this configuration is similar to the Landreman–Buller–Drevlak QH of the previous section, so the resulting weights are the same, with some of the threshold values slightly tuned. Changing thresholds instead of weights was found to give more predictable results. For the resulting coils, the normalized flux surface average of $|\boldsymbol {B} \boldsymbol {\cdot } \boldsymbol {\hat {n}}|$
QH configuration that was also optimized to satisfy the Mercier criterion, again using the initial non-planar optimization method with five coils per half-period. The weights and target values of the optimization yielding the best coils are presented in table 4. The boundary of this configuration is similar to the Landreman–Buller–Drevlak QH of the previous section, so the resulting weights are the same, with some of the threshold values slightly tuned. Changing thresholds instead of weights was found to give more predictable results. For the resulting coils, the normalized flux surface average of $|\boldsymbol {B} \boldsymbol {\cdot } \boldsymbol {\hat {n}}|$![]() (equation (2.10)) is $3.9 \times 10^{-3}$
(equation (2.10)) is $3.9 \times 10^{-3}$![]() . Figure 13 shows the comparison between the target surface and the surface achieved with the coils. Figure 14 shows the magnetic field at the boundary in Boozer coordinates. The coils themselves are shown in figure 15, along with the target surface. The green curves in figures 4(a) and 4(b) compare quasi-symmetry properties of the target configuration and the configuration achieved with the coils, again displaying similar quasi-symmetry degradation as the previous two configurations.
. Figure 13 shows the comparison between the target surface and the surface achieved with the coils. Figure 14 shows the magnetic field at the boundary in Boozer coordinates. The coils themselves are shown in figure 15, along with the target surface. The green curves in figures 4(a) and 4(b) compare quasi-symmetry properties of the target configuration and the configuration achieved with the coils, again displaying similar quasi-symmetry degradation as the previous two configurations.
Table 4. Weights placed on terms in the objective function as described in (2.2) as well as the target values and the achieved values averaged across the set of coils for the coil set of the $5\,\%$![]() volume-averaged $\beta$
volume-averaged $\beta$![]() QH Mercier criterion optimized configuration described in § 3.3.
QH Mercier criterion optimized configuration described in § 3.3.


Figure 13. Flux surface comparison of the QH $5\,\%$![]() volume-averaged $\beta$
volume-averaged $\beta$![]() configuration optimized to satisfy the Mercier criterion (red solid), and the surfaces produced by the coils (black dotted).
configuration optimized to satisfy the Mercier criterion (red solid), and the surfaces produced by the coils (black dotted).
With the same fast-particle tracing simulation set-up as in the previous sections, we obtain alpha-particle loss fractions of $3.7\,\%$![]() , $5.5\,\%$
, $5.5\,\%$![]() and $42\,\%$
and $42\,\%$![]() for particles launched at normalized toroidal flux $s=0.3$
for particles launched at normalized toroidal flux $s=0.3$![]() , $s=0.5$
, $s=0.5$![]() and $s=0.7$
and $s=0.7$![]() , respectively. For particles launched at the outermost radius, approximately $80\,\%$
, respectively. For particles launched at the outermost radius, approximately $80\,\%$![]() of trapped particles are lost over the $0.2$
of trapped particles are lost over the $0.2$![]() seconds simulated, resulting in the large loss fraction. For the stage I configuration, the corresponding loss fractions are $0.4\,\%$
seconds simulated, resulting in the large loss fraction. For the stage I configuration, the corresponding loss fractions are $0.4\,\%$![]() , $3.7\,\%$
, $3.7\,\%$![]() and $11.5\,\%$
and $11.5\,\%$![]() .
.
4 Conclusion
We have found a set of coils for the precise QH configuration of Landreman & Paul (Reference Landreman and Paul2022) that achieves an accurate reconstruction of the magnetic field with $\langle |\boldsymbol {B} \boldsymbol {\cdot } \boldsymbol {\hat {n}}| \rangle /\langle B \rangle = 0.0006$![]() while maintaining the targeted coil metrics described in § 2.2. These metrics are compared with NCSX and HSX metrics and shown to be considerably less complex, with this set of coils having half the maximum curvature and a quarter of the mean-squared curvature of NCSX. When perturbing the coils, we have shown that for $\sigma \leq 0.05,\mathrm {m}$
while maintaining the targeted coil metrics described in § 2.2. These metrics are compared with NCSX and HSX metrics and shown to be considerably less complex, with this set of coils having half the maximum curvature and a quarter of the mean-squared curvature of NCSX. When perturbing the coils, we have shown that for $\sigma \leq 0.05,\mathrm {m}$![]() , corresponding to coil perturbations of with an average amplitude of $0.13\,\mathrm {m}$
, corresponding to coil perturbations of with an average amplitude of $0.13\,\mathrm {m}$![]() , the fast-particle loss-fraction for particles launched from $s=0.3$
, the fast-particle loss-fraction for particles launched from $s=0.3$![]() generally stays below $1\,\%$
generally stays below $1\,\%$![]() . The coil set is thus robust to manufacturing error as outlined in § 2.3. The large allowance in coil perturbation amplitude of approximately $15\,\mathrm {cm}$
. The coil set is thus robust to manufacturing error as outlined in § 2.3. The large allowance in coil perturbation amplitude of approximately $15\,\mathrm {cm}$![]() is partly due to the configuration being at reactor scale and represents a small deviation in comparison to the length of the coils, which is approximately $35\,\mathrm {m}$
is partly due to the configuration being at reactor scale and represents a small deviation in comparison to the length of the coils, which is approximately $35\,\mathrm {m}$![]() .
.
We have shown that a reasonable number of planar coils alone cannot accurately generate the precise QH magnetic surfaces. The planar coils we found performed significantly worse than the non-planar coils for the given surface, despite having higher curvature and being allowed to have a smaller distances between the coils and surface. It is possible that other configurations may be more easily reproduced with planar coils.
In addition, we optimized coils for two $5\,\%$![]() volume-averaged $\beta$
volume-averaged $\beta$![]() configurations. Table 5 summarizes the coil metrics, achieved accuracy in reproducing the target boundary, as measured by (2.10), the two-term quasi-symmetry error and the fast-particle loss fractions. The finite-beta configurations have lower coil–coil and coil–surface distance, and larger values of curvature, but still achieve a less accurate reproduction of the plasma boundary when compared with the vacuum configuration. In particular, the coils for the Mercier-optimized configuration have roughly seven times larger field error (2.10) than the coils for the vacuum configuration.
configurations. Table 5 summarizes the coil metrics, achieved accuracy in reproducing the target boundary, as measured by (2.10), the two-term quasi-symmetry error and the fast-particle loss fractions. The finite-beta configurations have lower coil–coil and coil–surface distance, and larger values of curvature, but still achieve a less accurate reproduction of the plasma boundary when compared with the vacuum configuration. In particular, the coils for the Mercier-optimized configuration have roughly seven times larger field error (2.10) than the coils for the vacuum configuration.
Table 5. Summary of coil metrics, the accuracy metric (2.10), two-term quasi-symmetry error and fast-particle loss fraction from the $s=0.5$![]() surface for the configurations with coils targeting the Landreman–Paul precise QH, Landreman–Buller–Drevlak $\beta =5\,\%$
surface for the configurations with coils targeting the Landreman–Paul precise QH, Landreman–Buller–Drevlak $\beta =5\,\%$![]() QH and the $\beta =5\,\%$
QH and the $\beta =5\,\%$![]() QH optimized to satisfy the Mercier criterion. In parentheses are the corresponding values for the target configurations. See table 1 for a definitions of the symbols. NCSX and HSX included for reference.
QH optimized to satisfy the Mercier criterion. In parentheses are the corresponding values for the target configurations. See table 1 for a definitions of the symbols. NCSX and HSX included for reference.

Increasing beta to 5 % increases the quasi-symmetry error by approximately an order of magnitude compared with the vacuum configuration. Further optimizing for the Mercier criterion added another order of magnitude to the error. This increase occurs regardless of whether the configurations are fixed-boundary or reproduced with coils, with the coils adding roughly another order of magnitude in the quasi-symmetry error for each configuration. The fast-particle loss fractions are more difficult to interpret, but there is a $2\,\%$![]() to $3\,\%$
to $3\,\%$![]() absolute increase when comparing the finite-beta configurations produced by coils and their target configurations. The calculated fast-particle losses are still significantly lower than in existing stellarator devices (Landreman & Paul Reference Landreman and Paul2022; Bader et al. Reference Bader, Anderson, Drevlak, Faber, Hegna, Henneberg, Landreman, Schmitt, Suzuki and Ware2021).
absolute increase when comparing the finite-beta configurations produced by coils and their target configurations. The calculated fast-particle losses are still significantly lower than in existing stellarator devices (Landreman & Paul Reference Landreman and Paul2022; Bader et al. Reference Bader, Anderson, Drevlak, Faber, Hegna, Henneberg, Landreman, Schmitt, Suzuki and Ware2021).

Figure 14. Magnetic field $B$![]() on the boundary in Boozer coordinates. (a) $5\,\%$
on the boundary in Boozer coordinates. (a) $5\,\%$![]() volume-averaged $\beta$
volume-averaged $\beta$![]() QH configuration optimized to satisfy the Mercier criterion. (b) $B$
QH configuration optimized to satisfy the Mercier criterion. (b) $B$![]() produced by the coils presented in § 3.3.
produced by the coils presented in § 3.3.

Figure 15. Optimized coil set for the $5\,\%$![]() volume-averaged $\beta$
volume-averaged $\beta$![]() QH Mercier criterion optimized configuration (red).
QH Mercier criterion optimized configuration (red).
Acknowledgements
We thank the SIMSOPT team for their support. A.W. thanks J. Kappel for assistance with VMEC.
Editor P. Helander thanks the referees for their advice in evaluating this article.
Funding
This work was supported by the U.S. Department of Energy, Office of Science, Office of Fusion Energy Science, under award number DE-FG02-93ER54197. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility located at Lawrence Berkeley National Laboratory, operated under Contract No. DE-AC02-05CH11231 using NERSC award FES-ERCAP-mp217-2023. Additional computations were performed on the HPC systems Cobra and Raven at the Max Planck Computing and Data Facility (MPCDF).
Declaration of interests
The authors report no conflict of interest.
Appendix A. Planar coils for the Landreman–Paul configuration
To explore how well lower-complexity coils can reproduce the target magnetic field, we also consider whether the same plasma configuration can be produced with modular coils that are planar.
Each coil curve is taken to lie on a plane, with the distance of the coil from a central point described using a Fourier series. The rotation of the plane is described with a quaternion and the position of the central point is specified using Cartesian coordinates. Quaternion rotation is used to prevent gimbal locking during optimization. The quaternion has four elements $q_0 + i q_x + j q_y + k q_z$![]() which represent a rotation about some vector $\boldsymbol {u}$
which represent a rotation about some vector $\boldsymbol {u}$![]() through the central point:
through the central point:
where $\theta$![]() is the rotation about $\boldsymbol {u}$
is the rotation about $\boldsymbol {u}$![]() . We restrict $\boldsymbol {u}$
. We restrict $\boldsymbol {u}$![]() to be a unit vector; if it is not, the rotation would change the length of the curve.
to be a unit vector; if it is not, the rotation would change the length of the curve.

Figure 16. Planar coils optimized for the Landreman–Paul precise QH, with the target surface (red).
The position vector of a point along the coil before rotation is determined by


The quaternion rotation is then performed:

where the matrices in (A5) represent the position vector after rotation, the quaternion based rotation matrix as described by Shepperd (Reference Shepperd1978), the position vector before rotation defined by (A2), (A3), (A4), and a translation of the centre.
To attempt to find an adequately low-error coil set, we performed 115 optimizations while varying the weights and threshold values as described in (2.2). The weights and threshold values were varied around the previously found optimum values, so that we only consider planar coils of similar complexity to the non-planar coils.
The lowest normalized flux surface average of $|\boldsymbol {B} \boldsymbol {\cdot } \boldsymbol {\hat {n}}|$![]() (equation (2.10)) thus obtained was 0.0382. The average length of the resulting coils is 40.2 m, the maximum curvature and MSC were $0.397\,\mathrm {m}^{-1}$
(equation (2.10)) thus obtained was 0.0382. The average length of the resulting coils is 40.2 m, the maximum curvature and MSC were $0.397\,\mathrm {m}^{-1}$![]() and $0.577\,\mathrm {m}^{-1}$
and $0.577\,\mathrm {m}^{-1}$![]() , respectively, while the distance between coils and the distance from the coils to the surface were kept above 1.39 m and 0.96 m, respectively. The coils are shown in figure 16. A Poincaré plot of the resulting magnetic field is shown in figure 17. As seen from the Poincaré plot, the coils do a poor job of approximating the target surface. While producing this QH configuration with only planar modular coils does not appear possible, planar modular coils may be feasible for other plasma configurations, or perhaps if used along with windowpane coils. These possibilities are left for future work.
, respectively, while the distance between coils and the distance from the coils to the surface were kept above 1.39 m and 0.96 m, respectively. The coils are shown in figure 16. A Poincaré plot of the resulting magnetic field is shown in figure 17. As seen from the Poincaré plot, the coils do a poor job of approximating the target surface. While producing this QH configuration with only planar modular coils does not appear possible, planar modular coils may be feasible for other plasma configurations, or perhaps if used along with windowpane coils. These possibilities are left for future work.

Figure 17. Poincaré plot of the flux surfaces created by the planar coils optimized for the Landreman–Paul precise QH. Cross-sections are taken at standard toroidal angle $\phi = 0, 1/4$![]() period, $1/2$
period, $1/2$![]() period (from panel a–c). The solid red curves indicate the target plasma boundary.
period (from panel a–c). The solid red curves indicate the target plasma boundary.