Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T01:53:25.466Z Has data issue: false hasContentIssue false
  • English
  • Français

Phase mixing importance for both Landau instability and damping

Part of: PLA The Vlasov Equation

Published online by Cambridge University Press:  14 February 2017

D. D. A. Santos  and
Yves Elskens
D. D. A. Santos*
Affiliation:
Instituto de Física, Universidade de Brasília, CP: 04455, 70919-970 Brasília, DF, Brasil
Yves Elskens*
Affiliation:
Aix-Marseille Université and CNRS, UMR 7345 PIIM, case 322, campus Saint-Jérôme, FR-13013 Marseille, France
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We discuss the self-consistent dynamics of plasmas by means of a Hamiltonian formalism for a system of 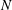$N$ near-resonant electrons interacting with a single Langmuir wave. The connection with the Vlasov description is revisited through the numerical calculation of the van Kampen-like eigenfrequencies of the linearized dynamics for many degrees of freedom. Both the exponential-like growth as well as damping of the Langmuir wave are shown to emerge from a phase mixing effect among beam modes, revealing unexpected similarities between the stable and unstable regimes.

Keywords

plasma dynamicsplasma instabilitiesplasma waves
Type
Research Article
Information
Journal of Plasma Physics , Volume 83 , Issue 1 , February 2017 , 705830106
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Belmont, G., Chust, Th., Mottez, F. & Hess, S. 2011 Landau and non-Landau linear damping: physics of the dissipation. Transp. Theory Stat. Phys. 40, 419–424.CrossRefGoogle Scholar
Bénisti, D. 2016 Envelope equation for the linear and nonlinear propagation of an electron plasma wave, including the effects of Landau damping, trapping, plasma inhomogeneity, and the change in the state of wave. Phys. Plasmas 23, 102105.Google Scholar
Bliokh, P., Sinitsin, V. & Yaroshenko, V. 1995 Dusty and Self-gravitational Plasmas in Space. Kluwer.Google Scholar
Bratanov, V., Jenko, F., Hatch, D. & Brunner, S. 2013 Aspects of linear Landau damping in discretized systems. Phys. Plasmas 20, 022108.Google Scholar
Brenig, L., Chaffi, Y. & Rocha Filho, T. M.2016 Long velocity tails in plasmas and gravitational systems. arXiv:1605.05981.Google Scholar
Brodin, G. 1997 Nonlinear Landau damping. Phys. Rev. Lett. 78, 1263–1266.Google Scholar
Brunetti, M., Califano, F. & Pegoraro, F. 2000 Asymptotic evolution of nonlinear Landau damping. Phys. Rev. E 62, 4109–4114.Google ScholarPubMed
Case, K. M. 1959 Plasma oscillations. Ann. Phys. 7, 349–364.Google Scholar
del Castillo-Negrete, D. 2002 Dynamics and self-consistent chaos in a mean field Hamiltonian model. In Dynamics and Thermodynamics of Systems with Long-range Interactions (ed. Dauxois, Th., Ruffo, S., Arimondo, E. & Wilkens, M.), Lecture Notes in Physics, vol. 602, pp. 407–436. Springer.Google Scholar
del Castillo-Negrete, D. & Firpo, M.-Ch. 2002 Coherent structures and self-consistent transport in a mean field Hamiltonian model. Chaos 12, 496–507.CrossRefGoogle Scholar
Chaffi, Y., Casta, R. & Brenig, L.2014 Effect of the fluctuations around mean field for $N$ -body systems with long range interactions. arXiv:1401.4746.Google Scholar
Dawson, J. M. 1960 Plasma oscillations of a large number of electron beams. Phys. Rev. 118, 381–389.CrossRefGoogle Scholar
Dawson, J. M. 1961 On Landau damping. Phys. Fluids 4, 869–874.Google Scholar
Dougherty, J. P. 1998 Van Kampen modes revisited. J. Plasma Phys. 59, 629–637.Google Scholar
Doveil, F., Escande, D. F. & Macor, A. 2005 Experimental observation of nonlinear synchronization due to a single wave. Phys. Rev. Lett. 94, 085003.Google Scholar
Elskens, Y. 2001 Finite- $N$ dynamics admit no traveling-wave solutions for the Hamiltonian XY model and single-wave collisionless plasma model. ESAIM: Proc. 10, 211–215.Google Scholar
Elskens, Y. 2005 Irreversible behaviours in Vlasov equation and many-body Hamiltonian dynamics: Landau damping, chaos and granularity in the kinetic limit. In Topics in Kinetic Theory (ed. Passot, Th., Sulem, C. & Sulem, P.-L.), Fields Institute Communications Series, vol. 46, pp. 89–108. American Mathematical Society.Google Scholar
Elskens, Y. & Escande, D. 2003 Microscopic Dynamics of Plasmas and Chaos. IOP.CrossRefGoogle Scholar
Elskens, Y., Escande, D. F. & Doveil, F. 2014 Vlasov equation and $N$ -body dynamics: how central is particle dynamics to our understanding of plasmas? Eur. Phys. J. D 68, 218.Google Scholar
Escande, D. F. 2010 Wave-particle interactions in plasmas: a qualitative approach. In Long-range Interacting Systems (ed. Dauxois, Th., Ruffo, S. & Cugliandolo, L. F.), Les Houches Summer School, vol. XC, pp. 469–506. Oxford University Press.Google Scholar
Escande, D. F., Doveil, F. & Elskens, Y. 2016 $N$ -body description of Debye shielding and Landau damping. Plasma Phys. Control. Fusion 58, 014040.CrossRefGoogle Scholar
Escande, D. F., Zekri, S. & Elskens, Y. 1996 Intuitive and rigorous derivation of spontaneous emission and Landau damping of Langmuir waves through classical mechanics. Phys. Plasmas 20, 3534–3539.CrossRefGoogle Scholar
Firpo, M.-Ch. & Elskens, Y. 1998 Kinetic limit of $N$ -body description of wave–particle self-consistent interaction. J. Stat. Phys. 93, 193–209.Google Scholar
Firpo, M.-Ch. & Elskens, Y. 2000 Phase transition in the collisionless damping regime for wave–particle interaction. Phys. Rev. Lett. 84, 3318–3321.Google Scholar
Firpo, M.-Ch. & Elskens, Y. 2001 O’Neil’s threshold for nonlinear Landau damping and phase transition in the wave–particle system. ESAIM: Proc. 10, 217–222.Google Scholar
Franklin, R. N., Hamberger, S. M. & Smith, G. J. 1972 Damping of finite-amplitude electron plasma waves in a collisionless plasma. Phys. Rev. Lett. 29, 915–917.CrossRefGoogle Scholar
van Kampen, N. G. 1955 On the theory of stationary waves in plasmas. Physica XXI, 949–963.Google Scholar
van Kampen, N. G. 1957 The dispersion equation for plasma waves. Physica XXIII, 641–650.CrossRefGoogle Scholar
Kandrup, H. E. 1998 Violent relaxation, phase mixing, and gravitational Landau damping. Astrophys. J. 500, 120–128.Google Scholar
Kiessling, M. K.-H. 2014 The microscopic foundation of Vlasov theory for jellium-like Newtonian $N$ -body systems. J. Stat. Phys. 155, 1299–1328.CrossRefGoogle Scholar
Lancellotti, C. & Dorning, J. J. 2003 Time-asymptotic wave propagation in collisionless plasmas. Phys. Rev. E 68, 026406.Google Scholar
Landau, L. D. 1946 On the vibrations of the electronic plasma. J. Phys. USSR 10, 25–34.Google Scholar
Malmberg, J. H. & Wharton, C. B. 1964 Collisionless damping of electrostatic plasma waves. Phys. Rev. Lett. 13, 184–186.Google Scholar
Malmberg, J. M. & Wharton, C. B. 1967 Collisionless damping of large-amplitude plasma waves. Phys. Rev. Lett. 19, 775–777.Google Scholar
Manfredi, G. 1997 Long-time behavior of nonlinear Landau damping. Phys. Rev. Lett. 79, 2815–2818.CrossRefGoogle Scholar
Mouhot, C. & Villani, C. 2010 Landau damping. J. Math. Phys. 51, 015204.Google Scholar
Mouhot, C. & Villani, C. 2011 On Landau damping. Acta Mathematica 207, 29–201; corr. fig. 391.CrossRefGoogle Scholar
Mynick, H. E. & Kaufman, A. N. 1978 Soluble theory of nonlinear beam–plasma interaction. Phys. Fluids 21, 653–663.Google Scholar
O’Neil, T. 1965 Collisionless damping of nonlinear plasma oscillations. Phys. Fluids 8, 2255–2262.Google Scholar
O’Neil, T. M., Winfrey, J. H. & Malmberg, J. H. 1971 Nonlinear interaction of a small cold beam and a plasma. Phys. Fluids 14, 1204–1212.Google Scholar
Onishchenko, I. N., Linetskiĭ, A. R., Matsiborko, N. G., Shapiro, V. D. & Shevchenko, V. I. 1970 Contribution to the nonlinear theory of excitation of a monochromatic plasma wave by an electron beam. Zh. Eksp. Teor. Fiz. Pis. Red. 12, 407–411; transl. JETP Lett. 12, 281–285.Google Scholar
Pen, U.-L. 1994 Modes of elliptical galaxies. Astrophys. J. 431, 104–108.Google Scholar
Ryutov, D. D. 1999 Landau damping: half a century with the great discovery. Plasma Phys. Control. Fusion 41 (Suppl. 3A), A1–A12; Proc. EPS Conf. Control. Fusion Plasma Phys. and Intl Cong. Plasma Phys. Prague 1998.CrossRefGoogle Scholar
Smereka, P. 2002 A Vlasov equation for pressure wave propagation in bubbly fluids. J. Fluid Mech. 454, 287–325.CrossRefGoogle Scholar
Tennyson, J. L., Meiss, J. D. & Morrison, P. J. 1994 Self-consistent chaos in the beam–plasma instability. Physica D 71, 1–17.Google Scholar
Vandervoort, P. O. 2003 On stationary oscillations of galaxies. Mon. Not. R. Astron. Soc. 339, 537–555.Google Scholar
Vekstein, G. E. 1998 Landau resonance mechanism for plasma and wind generated waves. Am. J. Phys. 66, 886–892.Google Scholar