Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-23T13:24:54.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Particle trajectories in Weibel filaments: influence of external field obliquity and chaos

Part of: Focus on Plasma Astrophysics

Published online by Cambridge University Press:  27 May 2020

A. Bret Open the ORCID record for A. Bret [Opens in a new window]  and
M. E. Dieckmann Open the ORCID record for M. E. Dieckmann [Opens in a new window]
A. Bret*
Affiliation:
ETSI Industriales, Universidad de Castilla-La Mancha, 13071Ciudad Real, Spain Instituto de Investigaciones Energéticas y Aplicaciones Industriales, Campus Universitario de Ciudad Real, 13071Ciudad Real, Spain
M. E. Dieckmann
Affiliation:
Department of Science and Technology (ITN), Linköping University, 60174Norrköping, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

When two collisionless plasma shells collide, they interpenetrate and the overlapping region may turn Weibel unstable for some values of the collision parameters. This instability grows magnetic filaments which, at saturation, have to block the incoming flow if a Weibel shock is to form. In a recent paper (Bret, J. Plasma Phys., vol. 82, 2016b, 905820403), it was found by implementing a toy model for the incoming particle trajectories in the filaments, that a strong enough external magnetic field 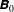$\unicode[STIX]{x1D63D}_{0}$ can prevent the filaments blocking the flow if it is aligned with them. Denoting by $B_{f}$ the peak value of the field in the magnetic filaments, all test particles stream through them if 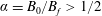$\unicode[STIX]{x1D6FC}=B_{0}/B_{f}>1/2$. Here, this result is extended to the case of an oblique external field 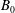$B_{0}$ making an angle 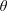$\unicode[STIX]{x1D703}$ with the flow. The result, numerically found, is simply 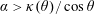$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D705}(\unicode[STIX]{x1D703})/\cos \unicode[STIX]{x1D703}$, where 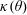$\unicode[STIX]{x1D705}(\unicode[STIX]{x1D703})$ is of order unity. Noteworthily, test particles exhibit chaotic trajectories.

Keywords

astrophysical plasmasplasma flowsplasma nonlinear phenomena
Type
Research Article
Information
Journal of Plasma Physics , Volume 86 , Issue 3 , June 2020 , 905860305
Copyright
© Cambridge University Press 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bret, A. 2014 Robustness of the filamentation instability in arbitrarily oriented magnetic field: full three dimensional calculation. Phys. Plasmas 21 (2), 022106.CrossRefGoogle Scholar
Bret, A. 2015 Particles trajectories in magnetic filaments. Phys. Plasmas 22, 072116.CrossRefGoogle Scholar
Bret, A. 2016a Hierarchy of instabilities for two counter-streaming magnetized pair beams. Phys. Plasmas 23, 062122.CrossRefGoogle Scholar
Bret, A. 2016b Particles trajectories in Weibel magnetic filaments with a flow-aligned magnetic field. J. Plasma Phys. 82, 905820403.CrossRefGoogle Scholar
Bret, A. & Dieckmann, M. E. 2017 Hierarchy of instabilities for two counter-streaming magnetized pair beams: influence of field obliquity. Phys. Plasmas 24 (6), 062105.CrossRefGoogle Scholar
Bret, A., Gremillet, L. & Dieckmann, M. E. 2010 Multidimensional electron beam-plasma instabilities in the relativistic regime. Phys. Plasmas 17, 120501.CrossRefGoogle Scholar
Bret, A. & Narayan, R. 2018 Density jump as a function of magnetic field strength for parallel collisionless shocks in pair plasmas. J. Plasma Phys. 84, 905840604.CrossRefGoogle Scholar
Bret, A. & Narayan, R. 2019 Density jump as a function of magnetic field for collisionless shocks in pair plasmas: the perpendicular case. Phys. Plasmas 26, 062108.CrossRefGoogle Scholar
Bret, A., Pe’er, A., Sironi, L., Sa̧dowski, A. & Narayan, R. 2017 Kinetic inhibition of magnetohydrodynamics shocks in the vicinity of a parallel magnetic field. J. Plasma Phys. 83, 715830201.CrossRefGoogle Scholar
Bret, A., Stockem, A., Fiuza, F., Ruyer, C., Gremillet, L., Narayan, R. & Silva, L. O. 2013 Collisionless shock formation, spontaneous electromagnetic fluctuations, and streaming instabilities. Phys. Plasmas 20 (4), 042102.CrossRefGoogle Scholar
Bret, A., Stockem, A., Narayan, R. & Silva, L. O. 2014 Collisionless Weibel shocks: full formation mechanism and timing. Phys. Plasmas 21 (7), 072301.CrossRefGoogle Scholar
Büchner, J. & Zelenyi, L. M. 1989 Regular and chaotic charged particle motion in magnetotaillike field reversals: 1. Basic theory of trapped motion. J. Geophys. Res. 94 (A9), 11821–11842.CrossRefGoogle Scholar
Cambon, B., Leoncini, X., Vittot, M., Dumont, R. & Garbet, X. 2014 Chaotic motion of charged particles in toroidal magnetic configurations. Chaos 24 (3), 033101.CrossRefGoogle ScholarPubMed
Chen, J. & Palmadesso, P. J. 1986 Chaos and nonlinear dynamics of single-particle orbits in a magnetotaillike magnetic field. J. Geophys. Res. 91, 1499–1508.CrossRefGoogle Scholar
Davidson, R. C., Hammer, D. A., Haber, I. & Wagner, C. E. 1972 Nonlinear development of electromagnetic instabilities in anisotropic plasmas. Phys. Fluids 15, 317.CrossRefGoogle Scholar
Dieckmann, M. E. & Bret, A. 2017 Simulation study of the formation of a non-relativistic pair shock. J. Plasma Phys. 83 (1), 905830104.CrossRefGoogle Scholar
Dieckmann, M. E. & Bret, A. 2018 Electrostatic and magnetic instabilities in the transition layer of a collisionless weakly relativistic pair shock. Mon. Not. R. Astron. Soc. 473 (1), 198–209.CrossRefGoogle Scholar
Forslund, D. W. & Shonk, C. R. 1970 Formation and structure of electrostatic collisionless shocks. Phys. Rev. Lett. 25, 1699–1702.CrossRefGoogle Scholar
Grassi, A., Grech, M., Amiranoff, F., Pegoraro, F., Macchi, A. & Riconda, C. 2017 Electron Weibel instability in relativistic counterstreaming plasmas with flow-aligned external magnetic fields. Phys. Rev. E 95 (2), doi:10.1103/PhysRevE.95.023203.Google ScholarPubMed
Jackson, J. D. 1998 Classical Electrodynamics. Wiley.Google Scholar
Kato, T. N. 2007 Relativistic collisionless shocks in unmagnetized electron–positron plasmas. Astrophys. J. 668 (2), 974.CrossRefGoogle Scholar
Lemoine, M., Gremillet, L., Pelletier, G. & Vanthieghem, A. 2019 Physics of Weibel-mediated relativistic collisionless shocks. Phys. Rev. Lett. 123, 035101.CrossRefGoogle ScholarPubMed
Lichtenberg, A. J. & Lieberman, M. A. 2013 Regular and Chaotic Dynamics. Springer.Google Scholar
Lyubarsky, Y. & Eichler, D. 2006 Are Gamma-ray bursts mediated by the Weibel instability? Astrophys. J. 647, 1250.CrossRefGoogle Scholar
Medvedev, M. V. & Loeb, A. 1999 Generation of magnetic fields in the relativistic shock of gamma-ray burst sources. Astrophys. J. 526, 697.CrossRefGoogle Scholar
Novo, A. S., Bret, A. & Sinha, U. 2016 Shock formation in magnetised electron–positron plasmas: mechanism and timing. New J. Phys. 18 (10), 105002.CrossRefGoogle Scholar
Ott, E. 2002 Chaos in Dynamical Systems. Cambridge University Press.CrossRefGoogle Scholar
Ram, A. K. & Dasgupta, B. 2010 Dynamics of charged particles in spatially chaotic magnetic fields. Phys. Plasmas 17 (12), 122104.CrossRefGoogle Scholar
Ryutov, D. D. 2018 Collisional and collisionless shocks. Plasma Phys. Control. Fusion 61 (1), 014034.Google Scholar
Sagdeev, R. Z. & Kennel, C. F. 1991 Collisionless shock waves. Sci. Am. 264 (4), 40–47.CrossRefGoogle Scholar
Shaisultanov, R., Lyubarsky, Y. & Eichler, D. 2012 Stream instabilities in relativistically hot plasma. Astrophys. J. 744, 182.CrossRefGoogle Scholar
Silva, L. O., Fonseca, R. A., Tonge, J. W., Dawson, J. M., Mori, W. B. & Medvedev, M. V. 2003 Interpenetrating plasma shells: near-equipartition magnetic field generation and nonthermal particle acceleration. Astrophys. J. 596, L121–L124.CrossRefGoogle Scholar
Spitkovsky, A. 2008 Particle acceleration in relativistic collisionless shocks: Fermi process at last? Astrophys. J. Lett. 682, L5–L8.CrossRefGoogle Scholar
Stockem, A., Lerche, I. & Schlickeiser, R. 2006 On the physical realization of two-dimensional turbulence fields in magnetized interplanetary plasmas. Astrophys. J. 651 (1), 584.CrossRefGoogle Scholar
Wiersma, J. & Achterberg, A. 2004 Magnetic field generation in relativistic shocks. An early end of the exponential Weibel instability in electron–proton plasmas. Astron. Astrophys. 428, 365–371.CrossRefGoogle Scholar
Yalinewich, A. & Gedalin, M. 2010 Instabilities of relativistic counterstreaming proton beams in the presence of a thermal electron background. Phys. Plasmas 17, 062101.CrossRefGoogle Scholar
Zel’dovich, I. A. B. & Raizer, Y. P. 2002 Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena. Dover Publications.Google Scholar