Article contents
Neoclassical, semi-collisional tearing mode theory in an axisymmetric torus
Published online by Cambridge University Press: 21 November 2017
Abstract
A set of layer equations for determining the stability of semi-collisional tearing modes in an axisymmetric torus, incorporating neoclassical physics, in the small ion Larmor radius limit, is provided. These can be used as an inner layer module for inclusion in numerical codes that asymptotically match the layer to toroidal calculations of the tearing mode stability index, 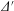 $\unicode[STIX]{x1D6E5}^{\prime }$. They are more complete than in earlier work and comprise equations for the perturbed electron density and temperature, the ion temperature, Ampère’s law and the vorticity equation, amounting to a twelvth-order set of radial differential equations. While the toroidal geometry is kept quite general when treating the classical and Pfirsch–Schlüter transport, parallel bootstrap current and semi-collisional physics, it is assumed that the fraction of trapped particles is small for the banana regime contribution. This is to justify the use of a model collision term when acting on the localised (in velocity space) solutions that remain after the Spitzer solutions have been exploited to account for the bulk of the passing distributions. In this respect, unlike standard neoclassical transport theory, the calculation involves the second Spitzer solution connected with a parallel temperature gradient, because this stability problem involves parallel temperature gradients that cannot occur in equilibrium toroidal transport theory. Furthermore, a calculation of the linearised neoclassical radial transport of toroidal momentum for general geometry is required to complete the vorticity equation. The solutions of the resulting set of equations do not match properly to the ideal magnetohydrodynamic (MHD) equations at large distances from the layer, and a further, intermediate layer involving ion corrections to the electrical conductivity and ion parallel thermal transport is invoked to achieve this matching and allow one to correctly calculate the layer
$\unicode[STIX]{x1D6E5}^{\prime }$. They are more complete than in earlier work and comprise equations for the perturbed electron density and temperature, the ion temperature, Ampère’s law and the vorticity equation, amounting to a twelvth-order set of radial differential equations. While the toroidal geometry is kept quite general when treating the classical and Pfirsch–Schlüter transport, parallel bootstrap current and semi-collisional physics, it is assumed that the fraction of trapped particles is small for the banana regime contribution. This is to justify the use of a model collision term when acting on the localised (in velocity space) solutions that remain after the Spitzer solutions have been exploited to account for the bulk of the passing distributions. In this respect, unlike standard neoclassical transport theory, the calculation involves the second Spitzer solution connected with a parallel temperature gradient, because this stability problem involves parallel temperature gradients that cannot occur in equilibrium toroidal transport theory. Furthermore, a calculation of the linearised neoclassical radial transport of toroidal momentum for general geometry is required to complete the vorticity equation. The solutions of the resulting set of equations do not match properly to the ideal magnetohydrodynamic (MHD) equations at large distances from the layer, and a further, intermediate layer involving ion corrections to the electrical conductivity and ion parallel thermal transport is invoked to achieve this matching and allow one to correctly calculate the layer 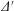 $\unicode[STIX]{x1D6E5}^{\prime }$.
$\unicode[STIX]{x1D6E5}^{\prime }$.
Keywords
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press 2017
References
- 4
- Cited by


