Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T15:02:07.790Z Has data issue: false hasContentIssue false
  • English
  • Français

Anomalous transport due to long-lived fluctuations in plasma Part 1. A general formalism for two-time fluctuations

Published online by Cambridge University Press:  13 March 2009

John A. Krommes  and
Carl Oberman
John A. Krommes
Affiliation:
Plasma Physics Laboratory, Princeton University and Institute for Advanced Study, Princeton, New Jersey 08540
Carl Oberman
Affiliation:
Plasma Physics Laboratory, Princeton University, Princeton, New Jersey 08540
Get access Rights & Permissions [Opens in a new window]

Abstract

A general formalism for describing two-time fluctuations in magnetized plasma is presented. Two-time expectations of one-body operators (phase functions) are written in terms of the phase space density autocorrelation function

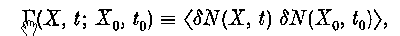
where δN is the fluctuation in the singular Klimontovich microdensity. It is shown that 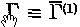is the first member of a set of two-time quantities

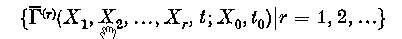
which collectively obeys the linearized BBGKY cumulant hierarchy in the (Xi, t) variables, with initial conditions successively smaller in the plasma parameter 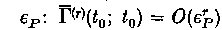. We study in detail the case of fluctuations in thermal equilibrium, although the general formalism holds also for the non-equilibrium case. To lowest order in εP, Γ obeys the linearized Vlasov equation. From this are recovered all of Rostoker's results for fluctuations excited by Cherenkov emission and absorbed by Landau damping, as well as a constructive proof of the test particle superposition principle. To first order, Γ obeys (in the Markovian approximation) the linearized Balescu-Guernsey-Lenard equation. For frequencies and wavenumbers in the hydrodynamic regime, the velocity moments of Γ obey linearized fluid equations with classical transport coefficients (i.e. essentially those computed by Braginskii in the 3-D case). It has been found that the classical theory is in disagreement with certain computer and laboratory experiments performed in strong magnetic fields. This defect is attributed to the absence in the classical theory of contributions to the collision operator, hence transport coefficients, of fluctuations long-lived on the Vlasov scale. Analogous difficulties arise in the theory of hydrodynamics in neutral fluids. To improve the plasma theory, a renormalization of the two-time hierarchy is proposed which sums selected terms from all orders in εP and thus treats the hydrodynamic fluctuations self-consistently. The resulting theory retains appropriate fluid conservation laws, thereby avoiding erroneous results encountered in certain diffusing orbit theories, when the fluid viscosity is indiscriminantly replaced by the test particle diffusion coefficient. In order to explain the results of the computer simulations, the theory is applied in part 2 to the problem of anomalous hydrodynamic contributions to the transport coefficients.

Type
Research Article
Information
Journal of Plasma Physics , Volume 16 , Issue 2 , October 1976 , pp. 193 - 227
Copyright
Copyright © Cambridge University Press 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Akasu, A. Z. & Duderstadt, J. J. 1969 Phys. Rev. 188, 479.CrossRefGoogle Scholar
Alder, B. J. & Wainwright, T. E. 1967 Phys. Rev. Lett. 18, 988.CrossRefGoogle Scholar
Balescu, R. 1960 Phys. Fluids, 3, 52.CrossRefGoogle Scholar
Balescu, R. & Senatorski, A. 1970 Ann. Phys. (N.Y.) 58, 587.CrossRefGoogle Scholar
Bartis, J. T. & Oppenheim, I. 1974 Phys. Rev. A10, 1263.CrossRefGoogle Scholar
Baus, M. 1973 Physica, 66, 421.CrossRefGoogle Scholar
Baus, M. 1975 Physica, A 79, 377.CrossRefGoogle Scholar
Baus, M. & Wallenborn, J. 1975 Phys. Lett. A 55, 90.CrossRefGoogle Scholar
Braginskii, S. I. 1965 Reviews of Plasma Physics (ed. Leontovich, M.), vol. I, p. 205. Plenum.Google Scholar
Bixon, M., Dorfman, J. R. & Mo, K. C. 1971 Phys. Fluids, 14, 1049.CrossRefGoogle Scholar
Dawson, J. M. 1968 Advances in Plasma Physics (ed. Simon, A. & Thompson, W. B.), vol. i, p. 1. Interscience.Google Scholar
Dawson, J. M., Okuda, H. & Carlile, R. N. 1971 Phys. Rev. Lett. 27, 491.CrossRefGoogle Scholar
Frieman, E. A. & Book, D. L. 1968 Phys. Fluids, 6, 1700.CrossRefGoogle Scholar
Green, M. S. 1954 J. Chem. Phys. 22, 398.CrossRefGoogle Scholar
Guernsey, R. 1960 Ph.D. Thesis, University of Michigan (unpublished).Google Scholar
Herring, J. R. 1965 Phys. Fluids, 8, 2219.CrossRefGoogle Scholar
Herring, J. R. 1973 Turbulence and Nonlinear Effects in Plasmas (ed. Keen, B. E. & Laing, E. W.), p. 305. Science Research Council, London.Google Scholar
Hinton, F. L. 1970 Phys. Fluids, 13, 857.CrossRefGoogle Scholar
Krommes, J. A. 1975 Ph.D. Thesis, Princeton University (unpublished).Google Scholar
Krommes, J. A. 1976 a Phys. Fluids, 19, 649.CrossRefGoogle Scholar
Krommes, J. A. 1976 b In preparation.Google Scholar
Krommes, J. A. & Oberman, C. 1976 J. Plasma Phys. 16, 229.CrossRefGoogle Scholar
Kubo, R. 1957 J. Phys. Soc. Japan, 12, 570.CrossRefGoogle Scholar
Kubo, R., Yokota, M. & Nakajima, S. 1957 J. Phys. Soc. Japan, 12, 1203.CrossRefGoogle Scholar
Kubo, R. 1962 J. Phys. Soc. Japan, 17, 1100.CrossRefGoogle Scholar
Landau, L. 1946 J. Phys. USSR, 10, 25.Google Scholar
Lee, Y. C. & Liu, C. S. 1973 Phys. Rev. Lett. 30, 361.CrossRefGoogle Scholar
Lenard, A. 1960 Ann. Phys. (N.Y.) 10, 390.CrossRefGoogle Scholar
Martin, P. C., Siggia, E. D. & Rose, H. A. 1973 Phys. Rev. A8, 423.CrossRefGoogle Scholar
Nakayama, T. & Dawson, J. M. 1967 J. Math. Phys. 8, 553.CrossRefGoogle Scholar
Okuda, H., Chu, C. & Dawson, J. M. 1975 Phys. Fluids, 18, 243.CrossRefGoogle Scholar
Okuda, H. & Dawson, J. M. 1972 Phys. Rev. Lett. 28, 1625.CrossRefGoogle Scholar
Okuda, H. & Dawson, J. M. 1973 Phys. Fluids, 16, 408.CrossRefGoogle Scholar
Pomeau, Y. 1972 Phys. Rev. A3, 1174.CrossRefGoogle Scholar
Pomeau, Y. & Resibois, P. 1975 Phys. Reports, 19C, 64.CrossRefGoogle Scholar
Rogister, A. & Oberman, C. 1968 J. Plasma Phys. 2, 33.CrossRefGoogle Scholar
Rogister, A. & Oberman, C. 1969 J. Plasma Phys. 3, 119.CrossRefGoogle Scholar
Rostoker, N. 1961 Nucl. Fusion, 1, 101.CrossRefGoogle Scholar
Rostoker, N. 1964 Phys. Fluids, 7, 491.CrossRefGoogle Scholar
Saleeby, B. B. & Lewis, M. B. 1971 Phys. Fluids, 14, 1931.CrossRefGoogle Scholar
Thompson, W. B. & Hubbard, J. 1960 Rev. Mod. Phys. 32, 714.CrossRefGoogle Scholar
Williams, E. 1973 Ph.D. Thesis, Princeton University (unpublished).Google Scholar