Published online by Cambridge University Press: 26 October 2018
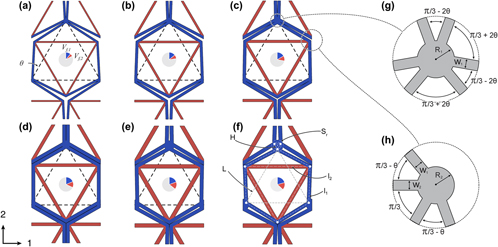
Low coefficient of thermal expansion (CTE) lattices occupy a unique area of property space. With such a system, it is possible to achieve relatively high stiffness, with opportunities to combine low thermal expansion and with a range of advantageous properties. Possibilities include combinations that are not rivaled by any bulk material, e.g., low CTE and high melting temperature, and low CTE with low conductivity. One design in particular, the UCSB Lattice, has biaxial stiffness very near theoretical upper bounds when the joints are pinned. Bonded lattices are found to inherit the near optimal performance of the parent pin-jointed design. Despite near optimal performance, however, stiffnesses and strengths are limited to a few percent of the relative property of the constituents. The local deformations necessary to accommodate low net CTE are similar to those of auxetic lattices, with similar behavior, having a low, zero, or negative tunable Poisson’s ratio. An investigative framework, including experiments, finite element, and analytical formulas, is used to construct these assessments.