Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-26T05:17:04.965Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite element modeling of nanoscale-enabled microinductors for power electronics

Published online by Cambridge University Press:  13 August 2018

Eric D. Langlois ,
Todd C. Monson ,
Dale L. Huber  and
John Watt Open the ORCID record for John Watt [Opens in a new window]
Eric D. Langlois*
Affiliation:
MEMS Technology Department, Sandia National Laboratories, Albuquerque, New Mexico 87185, USA
Todd C. Monson
Affiliation:
Nanoscale Sciences, Sandia National Laboratories, Albuquerque, New Mexico 87185, USA
Dale L. Huber
Affiliation:
Center for Integrated Nanotechnologies, Sandia National Laboratories, Albuquerque, New Mexico 87185, USA
John Watt
Affiliation:
Center for Integrated Nanotechnologies, Sandia National Laboratories, Albuquerque, New Mexico 87185, USA
*
a)Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

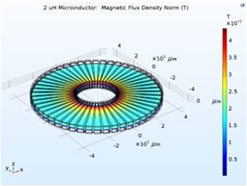
This article focuses on the finite element modeling of toroidal microinductors, employing first-of-its-kind nanocomposite magnetic core material and superparamagnetic iron nanoparticles covalently cross-linked in an epoxy network. Energy loss mechanisms in existing inductor core materials are covered as well as discussions on how this novel core material eliminates them providing a path toward realizing these low form factor devices. Designs for both a 2 μH output and a 500 nH input microinductor are created via the model for a high-performance buck converter. Both modeled inductors have 50 wire turns, less than 1 cm3 form factors, less than 1 Ω AC resistance, and quality factors, Q’s, of 27 at 1 MHz. In addition, the output microinductor is calculated to have an average output power of 7 W and a power density of 3.9 kW/in3 by modeling with the 1st generation iron nanocomposite core material.

Keywords

microelectronicsmicroelectromechanical (MEMS)magnetic properties
Type
Article
Information
Journal of Materials Research , Volume 33 , Issue 15: Focus Issue: Soft Magnetic Materials: Synthesis, Characterization, and Applications , 13 August 2018 , pp. 2223 - 2233
Copyright
Copyright © Materials Research Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

b)

This author was an editor of this journal during the review and decision stage. For the JMR policy on review and publication of manuscripts authored by editors, please refer to http://www.mrs.org/editor-manuscripts/.

References

REFERENCES

Chetvorno: Laminated core eddy currents (2015). Available at: https://commons.wikimedia.org/wiki/File:Laminated_core_eddy_currents.svg (accessed April 17, 2018).Google Scholar
Keeping, S.: Design trade-offs when selecting a high-frequency switching regulator (2015). Available at: https://www.digikey.com/en/articles/techzone/2015/feb/design-trade-offs-when-selecting-a-high-frequency-switching-regulator (accessed April 17, 2018).Google Scholar
Keeping, S.: The inductor’s role in completing a power module-based solution (2011). Available at: https://www.digikey.com/en/articles/techzone/2011/nov/the-inductors-role-in-completing-a-power-modulebased-solution (accessed April 17, 2018).Google Scholar
Watt, J., Bleier, G.C., Romero, Z.W., Hance, B.G., Bierner, J.A., Monson, T.C., and Huber, D.L.: Gram scale synthesis of Fe/FexOy core—shell nanoparticles and their incorporation into matrix-free superparamagnetic nanocomposites. J. Mater. Res. (2018). doi: 10.1557/jmr.2018.139.CrossRefGoogle Scholar
Mathuna, S.C.O., Donnell, T.O., Ningning, W., and Rinne, K.: Magnetics on silicon: An enabling technology for power supply on chip. IEEE Trans. Power Electron. 20, 3 (2005).CrossRefGoogle Scholar
Mathúna, C.Ó., Wang, N., Kulkarni, S., and Roy, S.: Review of integrated magnetics for power supply on chip (PwrSoC). IEEE Trans. Power Electron. 27, 11 (2012).CrossRefGoogle Scholar
Zhang, D.M. and Foo, C.F.: A simple method to estimate the magnetic field distribution due to current-carrying winding in toroidal core and its influence on the measurement of complex permeability and core losses. J. Magn. Magn. Mater. 191, 1–2 (1999).CrossRefGoogle Scholar
Lopez-Villegas, J.M., Vidal, N., and del Alamo, J.A.: Optimized toroidal inductors versus planar spiral inductors in multilayered technologies. IEEE Trans. Microw. Theor. Tech. 65, 2 (2017).CrossRefGoogle Scholar
Green, L.: RF-inductor modeling for the 21st century (2001). Available at: https://m.eet.com/media/1142818/19256-159688.pdf (accessed April 17, 2018).Google Scholar
Rozanov, E. and Ben-Yaakov, S.: A SPICE behavioral model for current-controlled magnetic inductors. In 23rd IEEE Convention of Electrical and Electronics Engineers in Israel (IEEE, Tel-Aviv, Israel, 2004); p. 338.Google Scholar
Taki, J., Bensetti, M., and Sadarnac, D.: SPICE-compatible high frequency physical modeling approach for an inductor. In 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia, Seoul, South Korea, 2015); pp. 176–181.Google Scholar
MATLAB: Nonlinear inductor: Model inductor with nonideal core (2015). Available at: https://www.mathworks.com/help/physmod/elec/ref/nonlinearinductor.html (accessed April 17, 2018).Google Scholar
Araghchini, M. and Lang, J.H.: Modeling and analysis of silicon-embedded MEMS toroidal inductors. J. Phys.: Conf. Ser. 476, 1 (2013).Google Scholar
Eroglu, A.: Complete modeling of toroidal inductors for high power RF applications. IEEE Trans. Magn. 48, 11 (2012).CrossRefGoogle Scholar
Paoli, G., Biro, O., and Buchgraber, G.: Complex representation in nonlinear time harmonic eddy current problems. IEEE Trans. Magn. 34, 5 (1998).CrossRefGoogle Scholar
Biglarbegian, M., Shah, N., Mazhari, I., and Parkhideh, B.: Design considerations for high power density/efficient PCB embedded inductor. In IEEE 3rd Workshop on Wide Bandgap Power Devices and Applications (WiPDA) (IEEE, Blacksburg, Virginia 2015); pp. 247–252.Google Scholar
Bi, Y. and Jiles, D.C.: Finite element modeling of an electrically variable inductor. IEEE Trans. Magn. 35, 5 (1999).CrossRefGoogle Scholar
Salas, R. and Pleite, J.: Nonlinear modeling of e-type ferrite inductors using finite element analysis in 2D. Materials 7, 8 (2014).CrossRefGoogle ScholarPubMed
Qin, Y. and Holmes, T.W.: A study on stray capacitance modeling of inductors by using the finite element method. IEEE Trans. Electromagn. Compat. 43, 1 (2001).Google Scholar
Ammouri, A., Salah, T.B., and Kourda, F.: Design and modeling of planar magnetic inductors for power converters applications. In 7th International Conference on Modelling, Identification and Control (ICMIC) (IEEE, Piscataway, New Jersey, 2015); p. 1.Google Scholar
Mickey, J.D.M., Madsen, P., Knott, A., and Andersen, M.A.E.: Design optimization of printed circuit board embedded inductors through genetic algorithms with verification by COMSOL (2013). Available at: https://www.comsol.com/paper/download/181351/madsen_paper.pdf (accessed April 17, 2018).Google Scholar
Schneider, T.A.H., Monster, J.D., Madsen, M.P., Knott, A., and Andersen, M.A.E.: Optimizing inductor winding geometry for lowest DC-resistance using livelink between COMSOL and MATLAB (2013). Available at: https://www.comsol.com/paper/download/181441/schneider_paper.pdf (accessed April 17, 2018).Google Scholar
COMSOL: Inductance of a power inductor (2017). Available at: https://www.comsol.com/model/inductance-of-a-power-inductor-1250 (accessed April 17, 2018).Google Scholar
Pokryvailo, A.: Calculation of inductance of sparsely wound toroidal coils (2016). Available at: https://www.comsol.com/paper/download/362301/pokryvailo_paper.pdf (accessed April 17, 2018).Google Scholar
COMSOL: Modeling a spiral inductor coil (2017). Available at: https://www.comsol.com/model/modeling-a-spiral-inductor-coil-21271 (accessed April 17, 2018).Google Scholar
Yang, C., Koh, K., Zhu, X., and Lin, L.: On-chip RF inductors with magnetic nano particles medium. In 16th International Solid-State Sensors, Actuators and Microsystems Conference (IEEE, Beijing, China, 2011); p. 2801.CrossRefGoogle Scholar
Chu, P.: Personal communication, COMSOL tech support, 2017. Available at: .Google Scholar
Frei, W.: Exploiting symmetry to simplify magnetic field modeling (2014). Available at: https://www.comsol.com/blogs/exploiting-symmetry-simplify-magnetic-field-modeling/ (accessed April 17, 2018).Google Scholar
Frei, W.: Modeling coils in the AC/DC module (2016). Available at: https://www.comsol.com/blogs/modeling-coils-in-the-acdc-module/ (accessed April 17, 2018).Google Scholar
Smith, S.: Evaluate your 3D inductor design with COMSOL multiphysics (2016). Available at: https://www.comsol.com/blogs/evaluate-your-3d-inductor-design-with-comsol-multiphysics/ (accessed April 17, 2018).Google Scholar
Frei, W.: How to choose between boundary conditions for coil modeling (2016). Available at: https://www.comsol.com/blogs/how-to-choose-between-boundary-conditions-for-coil-modeling/ (accessed April 17, 2018).Google Scholar
Sullivan, C.R., Li, W., Prabhakaran, S., and Lu, S.: Design and fabrication of low-loss toroidal air-core inductors. In IEEE Power Electronics Specialists Conference (IEEE, Orlando, Florida, 2007); p. 1754.Google Scholar
Phinney, J., Lang, J.H., and Perreault, D.J.: Multi-resonant microfabricated inductors and transformers. In IEEE 35th Annual Power Electronics Specialists Conference (IEEE, Aachen, Germany 2004); p. 4527.Google Scholar
COMSOL: COMSOL Multiphysics Reference Manual 5.3. (2017).Google Scholar
Araghchini, M.: (MEMS) toroidal magnetics for integrated power electronics. Ph.D. thesis, Massachusetts Institute of Technology, Cambridge, Massachusetts, 2013.Google Scholar
Taylor, B.N. and Kuyatt, C.E.: Guidelines for evaluating and expressing the uncertainty of NIST measurement results (1994). Available at: https://www.nist.gov/pml/nist-technical-note-1297 (accessed June, 2018).Google Scholar
Supplementary material: File

Langlois et al. supplementary material

Appendix

Download Langlois et al. supplementary material(File)
File 29.8 KB