Introduction
Recent thinning, acceleration, widening and grounding-line retreat of Pine Island Glacier (PIG) highlight this glacier’s dramatic changes and make it one of the most interesting glaciers in the Amundsen Sea sector of Antarctica, itself one of the ice sheet’s most dynamic areas (Reference RignotRignot, 1998, Reference Rignot2008; Reference BindschadlerBindschadler, 2002; Reference Shepherd, Wingham and MansleyShepherd and others, 2002; Reference Joughin, Rignot, Rosanova, Lucchitta and BohlanderJoughin and others, 2003; Reference ThomasThomas and others, 2004; Reference Scott, Gudmundsson, Smith, Bingham, Pritchard and VaughanScott and others, 2009). The observed changes have contributed to an accelerating rate of ice loss from this sector of the West Antarctic ice sheet from 41 ± 27 Gt a−1 in 1996 to 90 ± 27 Gt a−1 in 2006, delivering the largest ice contribution to rising global sea level of any Antarctic region (Reference RignotRignot, 2008). The spatial patterns of change within the PIG catchment basin and in neighboring glaciers suggest that the ocean is driving these changes (Reference Payne, Vieli, Shepherd, Wingham and RignotPayne and others, 2004). Direct observations of glacier acceleration following ice-shelf removal on the Antarctic Peninsula have been reported (Reference Rignot, Casassa, Gogineni, Krabill, Rivera and ThomasRignot and others, 2004; Reference Scambos, Bohlander, Shuman and SkvarcaScambos and others, 2004) and a visco-plastic ice-flow model capable of matching observations of PIG acceleration and thinning further strengthens the view that basal melt rate plays a key role in the recent dynamical change in PIG (Reference Joughin, Smith and HollandJoughin and others, 2010).
PIG feeds an ice shelf >1 km thick at its grounding line which thins to about 300 m at the calving front. Ice shelves in the Amundsen Sea region experience higher basal melt rates than most other portions of the Antarctic coast due in large measure to the influence of upwelled relatively warm Circumpolar Deep Water (CDW) that floods onto the continental shelf from the deeper ocean (Reference Jacobs, Hellmer and JenkinsJacobs and others, 1996). Melting caused by this ‘mode-2’ circulation (Reference Jacobs, Hellmer, Doake, Jenkins and FrolichJacobs and others, 1992) is enhanced further along the grounding line (the place where the ice first loses contact with the bed) of the deepest ice by the pressure-dependent decrease of the freezing point that increases the temperature difference between the water and ice.
Reference Thoma, Jenkins, Holland and JacobsThoma and others (2008) have established that variability of atmospheric winds in the Amundsen Sea region causes substantial changes in the amount of CDW that upwells onto the continental shelf, approaches PIG and flows beneath its ice shelf. In this paper, we analyze satellite imagery and airborne observations of the PIG ice shelf to investigate the connection between ice-thickness variations created at a spatially limited region of the grounding line and atmospheric wind variability. As others have found, derived melt rates are extremely high and spatially variable, even along the grounding line. We also infer that only a small percentage of the heat available in the ocean water is actually used to melt ice before the water exits the ice-shelf cavity. Both the seasonal and interannual variability of melt are large, indicating a responsive system.
Data
Imagery
Satellite imagery of the PIG ice shelf indicates that it is ∼35 km across at its upstream junction with the glacier, a sinuous and shifting grounding line (Fig. 1). The shelf flows generally westward, gradually turning about 10° to the north over a distance of 50–65 km and widening another 5 km before reaching the calving ice front. Regions of intense crevassing stretch downstream from numerous sites of initiation on the glacier or at either side of the glacier’s grounding zone. Larger-scale features are also apparent. Periodic ridges and troughs with amplitudes of 10–15 m are generally aligned with the direction of motion but occasionally are distorted or interrupted by periodic transverse-oriented topography, particularly along the center of the ice shelf (Fig. 1). Sequences of shorter ridges and troughs angled to flow also occur. The most prominent of these series occurs on the south side of the ice shelf and stretches the full length of the ice shelf. A shorter set of angled undulations occurs on the north side of the ice shelf nearer the grounding line, seen more clearly in Figure 2 which is a higher-resolution image collected with a different sun azimuth than Figure 1.

Fig. 1. Satellite imagery of the PIG ice-shelf area extracted from the Moderate Resolution Imaging Spectroradiometer (MODIS) Mosaic of Antarctica (http://nsidc.org/data/nsidc-0280.html). Collection date is approximately February 2004. Multicolored lines labeled 1–4 are data flight-lines the profiles of which are illustrated in Figures 4–7. Color along line represents distance and is consistent with Figures 4–7 to aid in associating position in those figures with image. Solid color curves are grounding lines mapped at different epochs: red, 1992; green, 1996; blue, 2000; and yellow, 2009 (Reference RignotRignot 1998, Reference Rignot2008; Reference Joughin, Smith and HollandJoughin and others, 2010). White lines are Autosub tracks (Reference JenkinsJenkins and others, 2010). White triangles indicate the January 2005 grounding-line positions along each flight-line as determined from Figures 4–7. Inset shows the location of the PIG ice shelf on a map of the Antarctic continent.
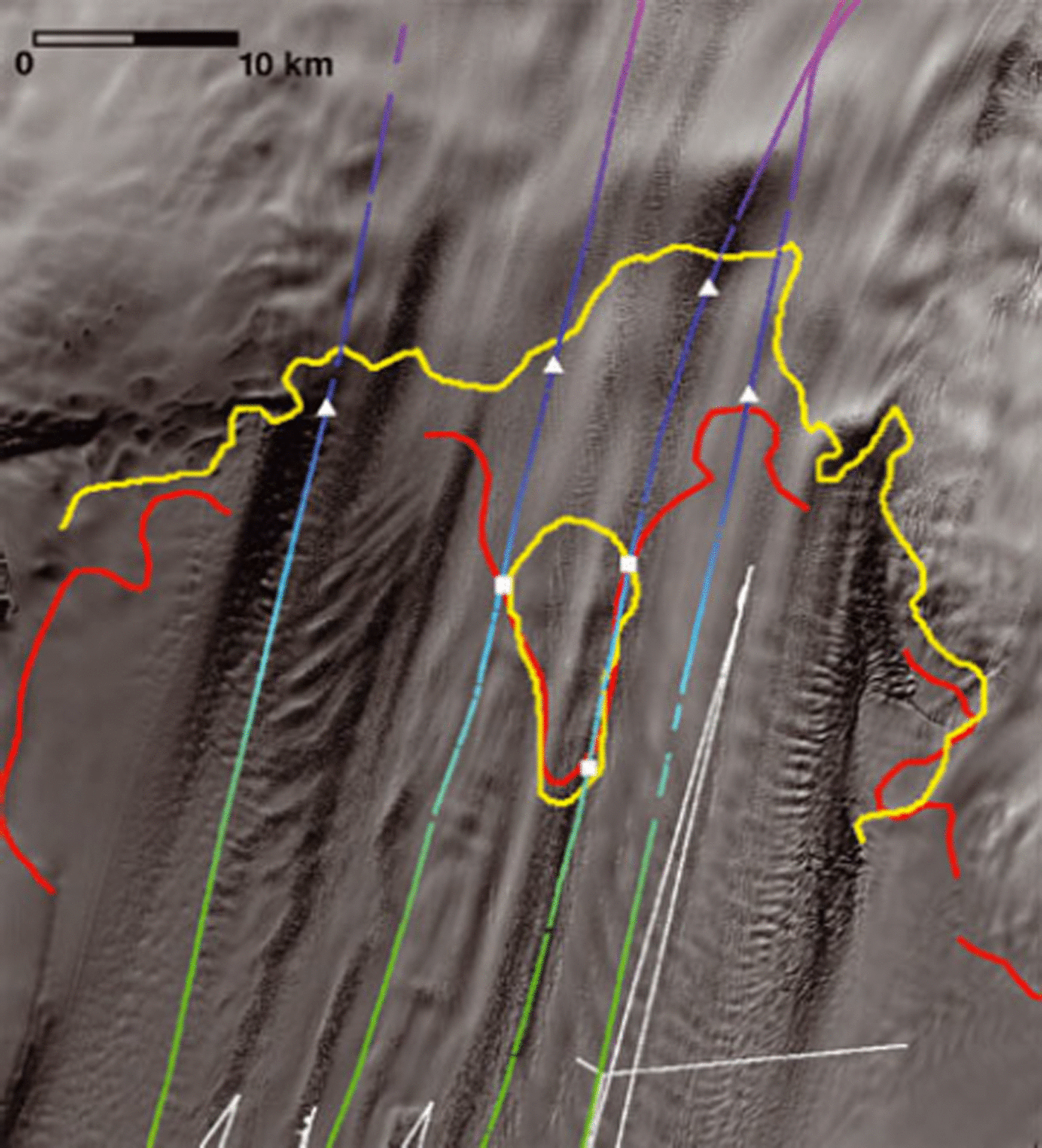
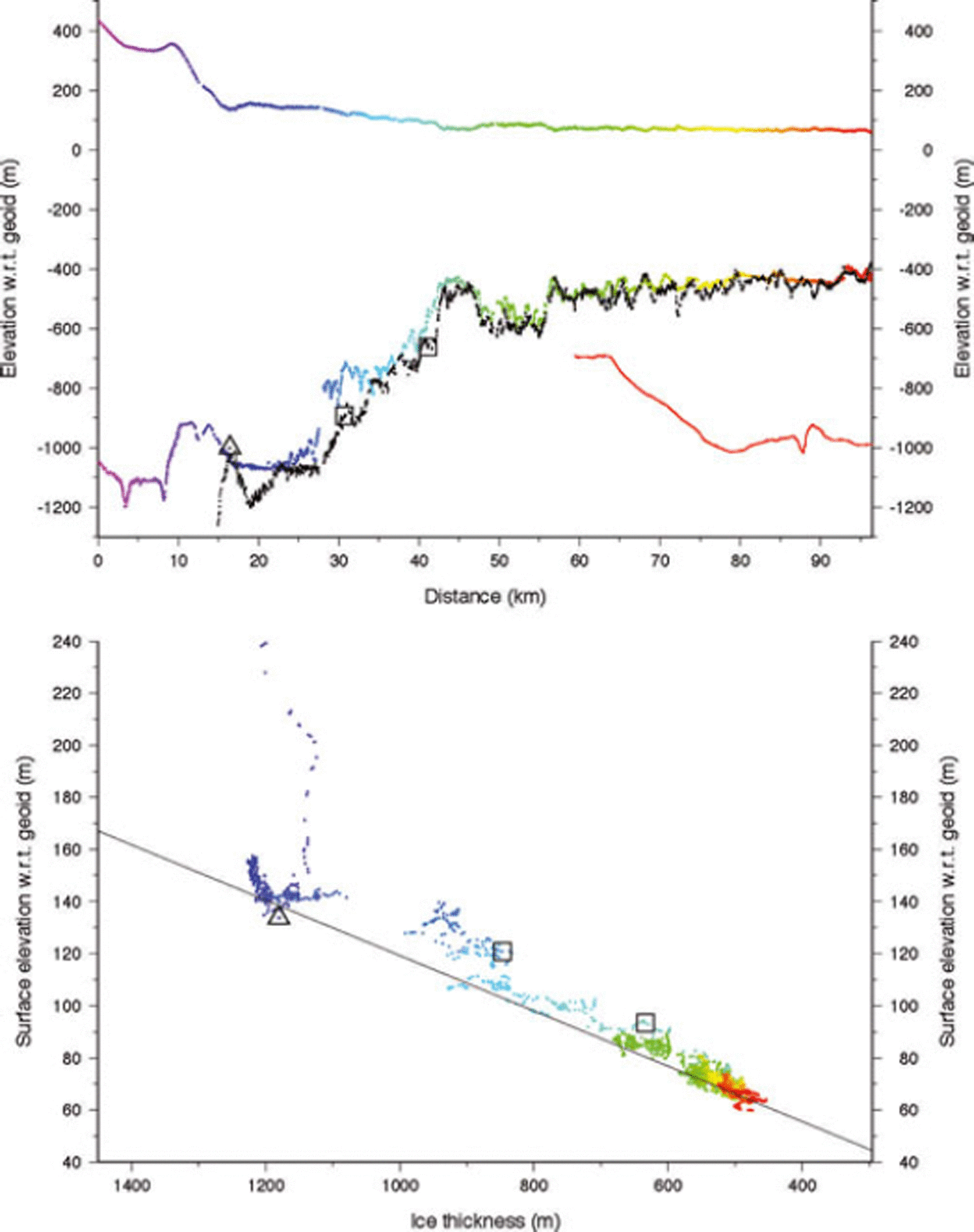
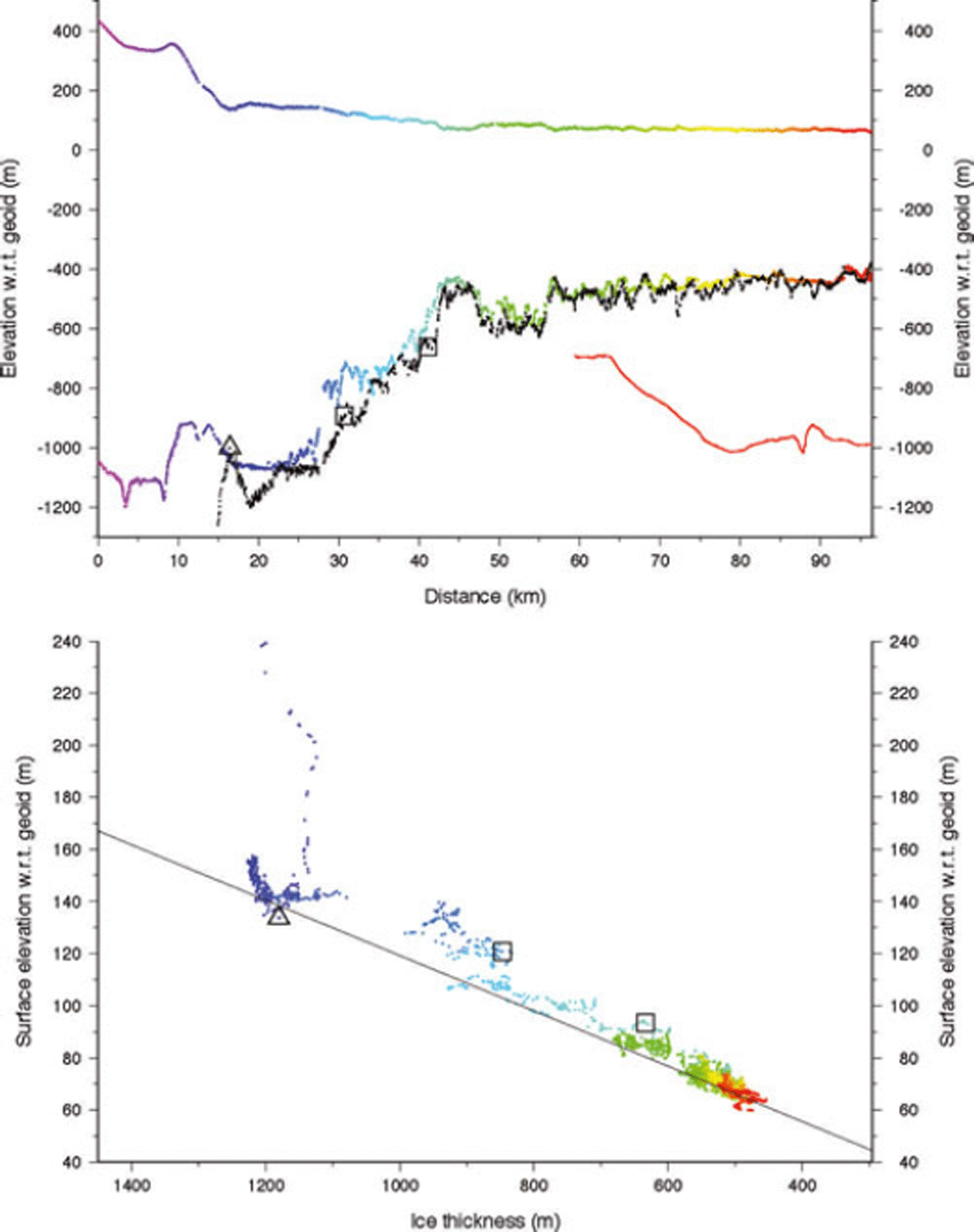
Fig. 2. Landsat imagery of the grounding-line area of PIG and ice shelf composited from imagery collected on 1 January 2005 (75%), 10 January 2005 and 8 January 2005, close to the date of airborne data acquisition. All images are averaged to 60 m pixel resolution. Grounding-line positions shown are for 1992 (red) and 2009 (yellow). Multicolored lines are airborne flight-lines, and white lines are Autosub tracks (as in Fig. 1). White triangles indicate the January 2005 grounding-line positions along each flight-line as determined from Figures 4–7. White squares indicate intersections of flight-lines with the plotted grounding lines and are included in Figures 5 and 6.
The grounding line of PIG has changed over the past 20 years and its locations, mapped at various epochs using interferometric synthetic aperture radar analyses, are included in Figure 1 (Reference RignotRignot, 1998, Reference Rignot2008; Reference Joughin, Smith and HollandJoughin and others, 2010). The general retreat of the grounding line has been attributed to ice-shelf thinning and glacier ungrounding (references cited above).
Changes in the character of surface features can be associated with changes in ice flow, including changes in the nature of the grounding line (e.g. Reference Fahnestock, Scambos, Bindschadler and KvaranFahnestock and others, 2000; Reference BindschadlerBindschadler, 2002; Reference JenkinsJenkins and others, 2010). Figure 3 also shows the image used in Figure 1 collected in February 2004, but with overlays that connect features across the ice shelf that passed the grounding line at the same time. In addition to the 1992 and 1996 grounding lines appearing in their mapped locations, the February 2004 positions of the ice that passed the grounding line in 1992 and 1996 are also indicated. The velocity field used for this calculation used linear temporal interpolations of velocity fields measured in 1996 and 2006 (personal communication from I. Joughin and E. Reference RignotRignot, 2008). These two epochs are chosen because between these dates Reference RignotRignot (1998) reported a dramatic recession of the grounding line and acceleration of the ice speed. Examination of Figure 3 reveals that the advected position of the 1996 grounding line demarcates a change in many of the surface flow features. On the north side of the glacier, ice upstream of the 1996 grounding line is more extensively crevassed and the series of regularly spaced angled linear undulations begins. In the central part of the ice shelf, shorter and more irregularly spaced undulations occur where there are none in ice downstream of this boundary. On the south side of the ice shelf, the surface topography is dominated by a regularly spaced set of undulations angled to flow, extending from the ice-shelf front to near the grounding line, but even within this series the undulations become shorter upstream of the boundary of the advected 1996 grounding-line ice. Our inference from these observations is that the changes in grounding-line position and flow rate are related to a significant change in the ice shelf at this time. Later we associate these changes in surface features with interactions between the ice shelf and the underlying ocean.

Fig. 3. MODIS image collected in February 2004 (from Fig. 1), with grounding-line positions for 1992 (solid red curve) and 1996 (solid green curve) indicated. Dashed lines are computed February 2004 positions of ice that was at the grounding line in 1992 (red) and 1996 (green).
Airborne data
In the 2004/05 field season, airborne studies of the PIG catchment area included four flights along the PIG ice shelf aligned roughly with the flow direction (Fig. 1). Figure 2 is a composite of three Landsat images all collected during the aerogeophysical campaign. Surface elevation, ice-thickness and gravity data were acquired on each flight as described in Reference VaughanVaughan and others (2006). The geometry and hydrostatic character of each of these profiles are discussed below and illustrated in Figures 4–7.

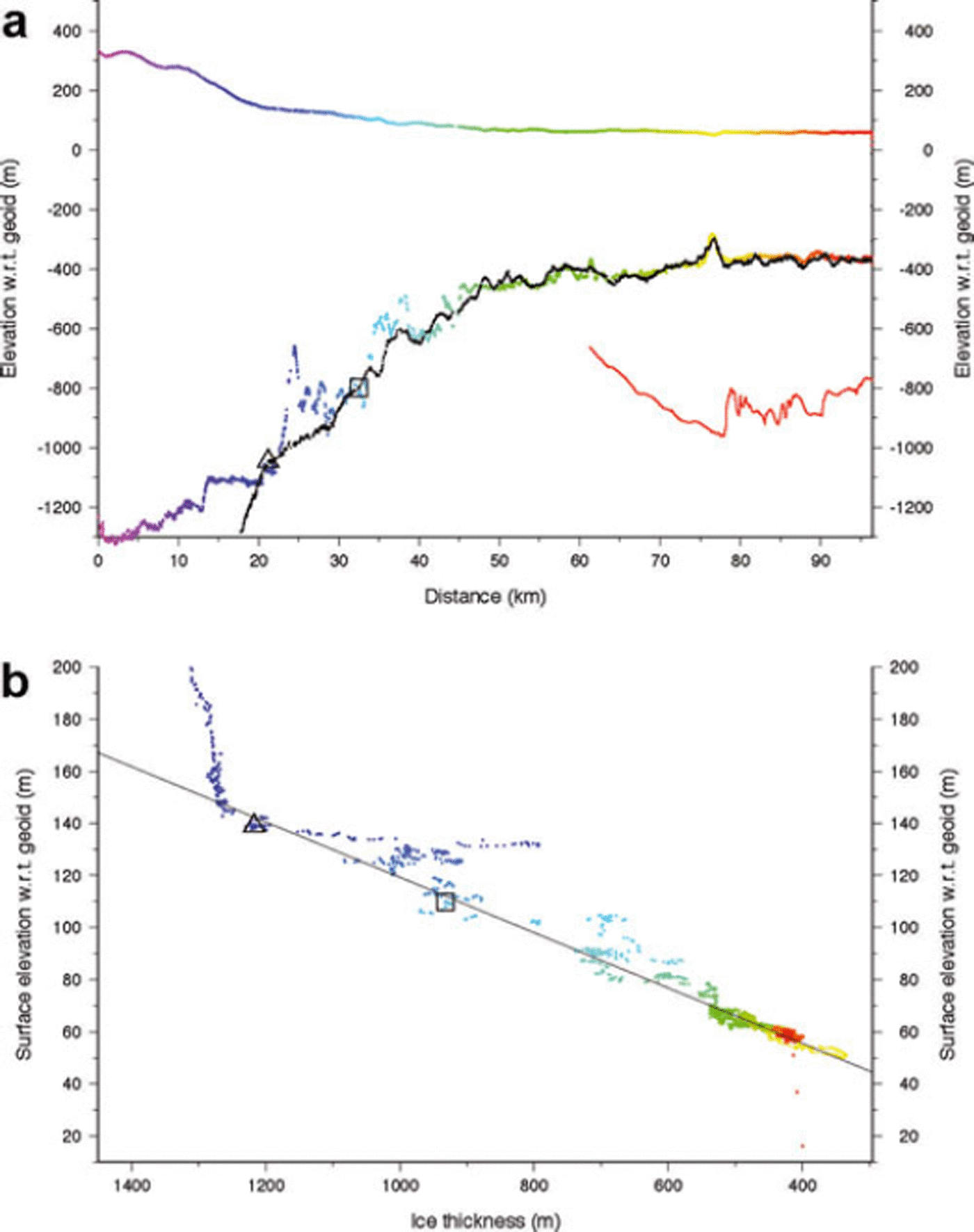
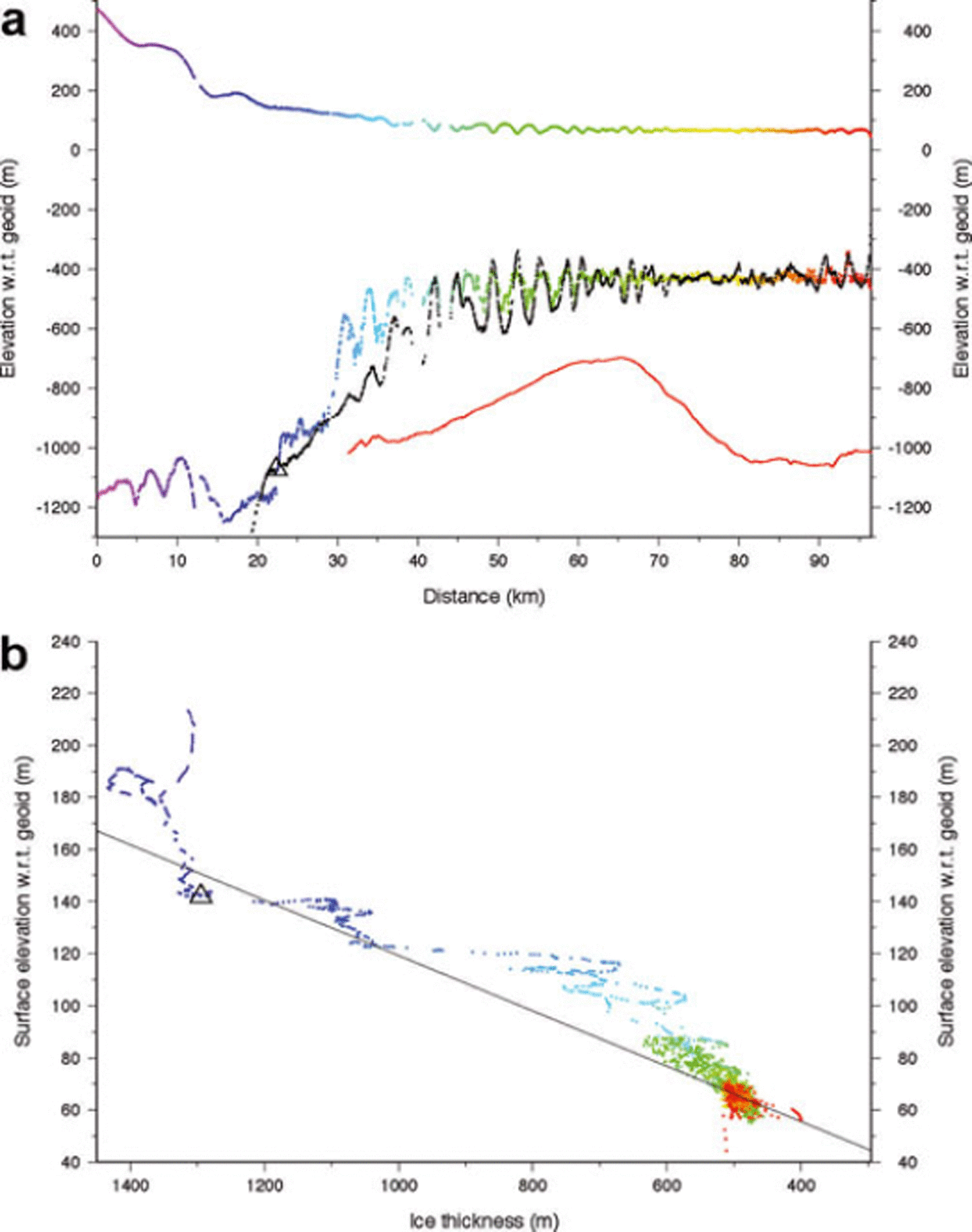
Fig. 4. (a) Multicolored profiles are ice surface and ice-bottom elevations (with respect to the EGM96 geoid) along profile 1 (see Fig. 1 for location) measured by airborne radar during the 2004/05 austral summer. Colors indicate distance from an arbitrary origin upstream to allow correlation with (b) and Figure 1. Black points present ice-bottom profile based on measured surface elevations and the hydrostatic condition given in Equation (1) (and the line in (b)). Red curve is nearby bathymetric profile from Autosub (personal communication from Reference JenkinsA. Jenkins, 2010). Black open triangle is grounding line determined from these data. (b) Surface elevation vs ice thickness for the measured (colored) elevation profiles in (a). Line is derived from Equation (1) and represents hydrostatic equilibrium for ice with an extra column of air 14.6 m thick as described in the text. Floating points lie on or near this line and grounded points plot above this line.
The northernmost profile, 1, is shown in Figure 4. Figures 1 and 2 illustrate that it enters the ice shelf near the northern edge of PIG and continues downstream, coming close to the series of surface undulations angled to ice flow and discussed earlier. The vertical profile along this flight-line shows grounded ice >1000 m thick with a rough surface flowing across an equally rough bottom and thinning rapidly to a nearly uniformly 550 m thick ice shelf extending for >40 km before two thinner portions appear over the last 25 km. Although the profile missed the major surface undulations, there is a set of smaller-amplitude shorter-wavelength surface undulations apparent in the data. Evidence of these can be seen in the Landsat image (Fig. 2). Nearer the downstream end, the much longer-wavelength surface undulations are related to the curved trough seen crossing the yellow portion of profile 1 in Figure 1.
The hydrostatic condition of the ice along this profile is examined by applying the relationship

where Z s is the surface elevation (referenced to the Earth Gravity Model (EGM96) geoid), H is the ice thickness and ρ w and ρ i are the densities of sea water and ice, 1026 and 917 kg m−3, respectively. The parameter h a is the equivalent thickness of air contained in firn. The spatial variation of this firn–air correction term has been modeled by Reference Van den Broeke, van de Berg and van MeijgaardVan den Broeke and others (2008). We interpolate their values to this location and obtain a value of 14.6 m. Assigning these parameter values to the terms in Equation (1) determines the offset and slope of the line shown in Figure 4b. Floating points should lie on or near this line, while grounded points will plot above the line. In addition, Equation (1) can be used to calculate the ‘flotation’ ice thickness corresponding to a given surface elevation. This method is used to calculate the ‘hydrostatic ice bottom’ shown in Figure 4a as a set of black points. The data illustrate a distinct transition from grounded ice to floating ice at a distance coordinate of 27 km (the origin of this axis is not significant); this is the grounding line at the epoch defined by the flight, and its position is included in Figures 1 and 2. Downstream of this location, the ice is floating freely, indicated by these points plotting close to the hydrostatic line in Figure 4b.
The next flight southward, profile 2 (Fig. 5), exhibits a more gradual thinning along most of its length with a smooth upper surface. Figure 1 confirms that this flight-line encounters very few surface undulations. The grounded glacier is >1200 m thick when it reaches initial flotation at distance 21 km. Over the next 25 km downstream, the measured surface and ice-bottom data are near, but not coincident with, hydrostatic equilibrium. This confirms the presence of a lightly grounded ‘ice plain’ as discussed in Reference Corr, Doake, Jenkins and VaughanCorr and others (2001). Figure 2 illustrates a 12 km retreat of the grounding line from 1992 to 2009, with the position interpreted from the 2005 airborne data being much closer to the 2009 position. However, at km 32 the profile passes the isolated grounded region in the 2009 mapping coincident with the 1992 grounding line (see Fig. 2 and open squares in Fig. 5). Nearby grounding makes crevassing more likely.
Careful reinterpretation of the airborne radar records for these flights reveals that the shapes of the thinner portions of the basal undulations, especially those nearest the grounding line, are due in large measure to the presence of basal crevasses deeply incised into the underside of the ice shelf. Reflection hyperbolae in the unmigrated radar data arising from the uppermost vertices of these crevasses were sometimes misinterpreted as ice voids in the ice-shelf basal ice. In some cases, these reflection hyperbolae were strong enough to hide the true ice-bottom reflection. This means that on a horizontal scale of several ice thicknesses, ice thickness was underestimated, an effect that would make a grounded area appear to be floating. For this particular profile, the shape of the ice bottom between km 23 and km 30 and between km 35 and km 40 resembles a set of unmigrated reflection hyperbolae from a few point reflectors. We expect the ice was thicker in these sections, but we cannot be confident that there was, or was not, an ice plain in this area in January 2005.
Moving further south to profile 3 (Fig. 6), this ice exhibits features very similar to profile 2 except that the flight path follows a band of intense surface crevasses over the first half of its length (Figs 1 and 2). The surface is quite steep just upstream of the grounding line, with many smaller surface undulations along the rest of the profile. Ice upstream of km 17 is firmly grounded although the actual grounding line may not occur until km 23. The flight-line follows the edge of the extended peninsula of grounded ice that is most recently mapped as an isolated grounded area (see Fig. 2 and open squares in Fig. 6). Again, basal crevasses are likely, as is the possibility of an ice plain as a transient condition in early 2005, before the separation of this grounded area in the 2009 grounding-line mapping. From km 41 onward the ice appears to be unequivocally afloat, with ice thicknesses between 450 and 680 m. The large thin region centered at km 45 is probably due to the presence of the grounded promontory immediately upstream, either by tensile stretching of the ice or enhanced flow at the grounding line there.
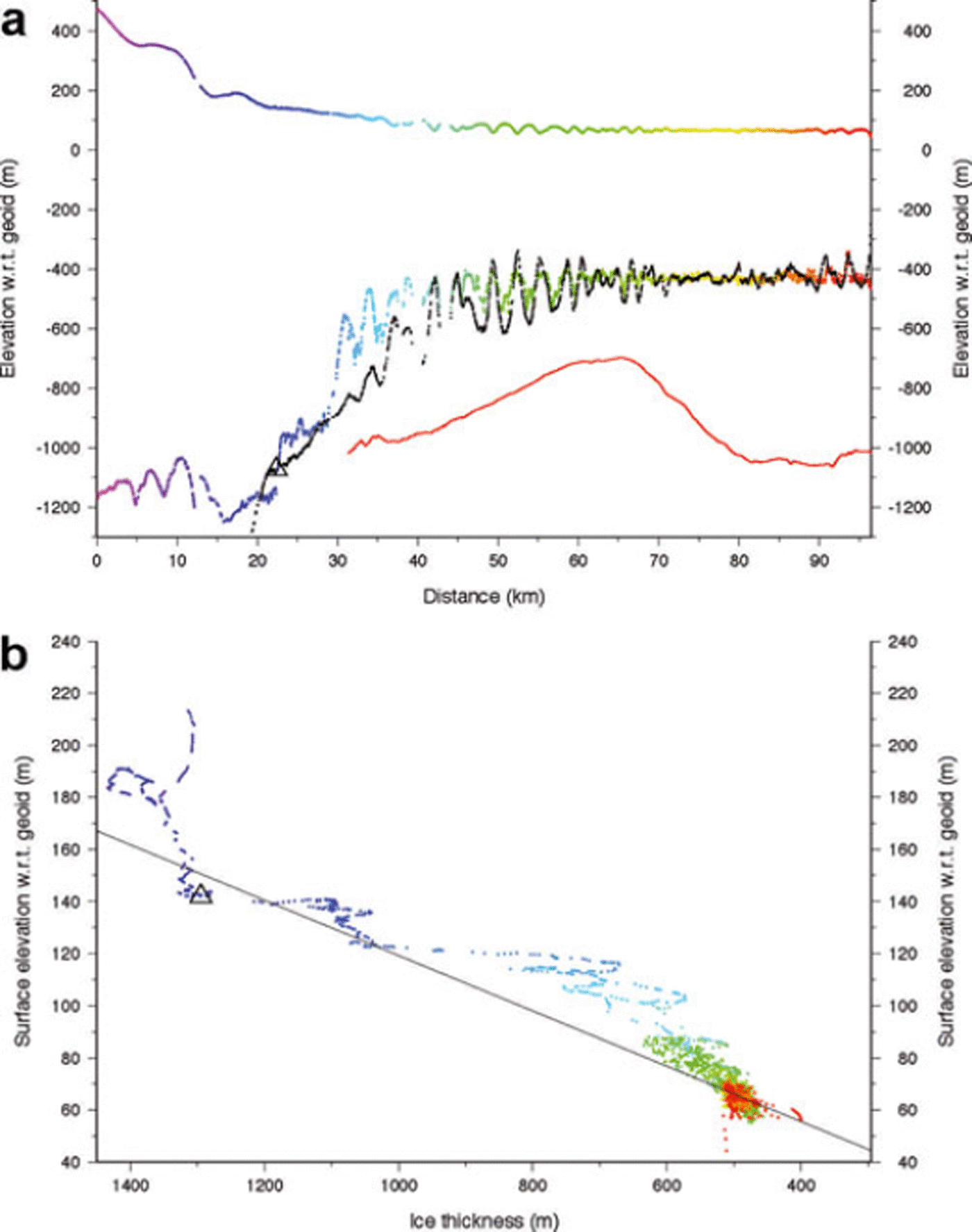
The southernmost profile, 4 (Fig. 7), traverses a region where grounding-line retreat was less than it was for profiles 2 and 3 and it runs more parallel to the 2009 grounding-line position (Fig. 2). The surface is generally free of crevasses and the ice is nearly 1300 m thick at the 2005 grounding line.
What makes this profile most distinct from the others is its inclusion of a series of prominent surface undulations discussed earlier (see Fig. 1). These occur between km 35 and km 70. The undulations do not appear downstream of km 70, but Figure 1 shows that this is because the band of undulations turns northward, veering away from the flightline’s straighter course, so although the undulations persist to the ice-shelf front, they were not sampled by the downstream portion of the profile 4 data. Downstream from this point of departure, the downstream segment of this profile is similar to the others already discussed, with the addition that two flow-transverse surface troughs are sampled very near the ice front (see Fig. 1).
Figure 7 shows that these undulations appear not only in the surface elevations, but also in the bottom elevations, and the surface and bottom undulations are aligned so that surface crests match bottom keels. The ‘hydrostatic’ ice bottom (calculated from Equation (1) and the surface elevations) also emphasizes this alignment and, although the amplitude of the hydrostatically calculated bottom undulations is slightly larger than measured, the average depth agrees, indicating the absence of a bias to either the surface measurements or the obscuration of deeper keels. Surface undulation amplitudes are in the range 10–15 m, with the bottom undulations amplified to 100–150 m.
The grounding line of profile 4 occurs at approximately km 22 (Fig. 7). Between this point and the beginning of the strong surface undulations at km 35 the differences between the measured ice bottom and the ‘hydrostatic’ ice bottom are often >100 m, the largest seen on any of the profiles. The shape of the measured ice bottom here is suggestive of reflection hyperbolae from basal crevasses. A complete masking of a much deeper ice bottom cannot be discounted. Less extreme examples are seen in profiles 2 and 3 (Figs 5 and 6). There are other possibilities. The possible existence of an ice plain cannot be rejected. A lower column density would raise the calculated ice bottom but only by a few meters and it is unclear why lower densities would be limited to this region of this profile. These large basal undulations are overlain by matching inverted surface undulations (just like those downstream), but of much smaller amplitude; this is seen most easily in the hydrostatic bottom (black points in Fig. 7) that amplifies slight variations in the surface elevation data. Here we suggest, and later defend, our interpretation that these basal undulations are initiated as basal crevasses formed in ice that recently transited the grounding line and are enlarged by melting. Their initial depth and width are unknown, due to the obscuring nature of the radar hyperbolae created by the deep incisions into the ice, but their subdued surface topography is due, in part, to the supporting beam stresses of the adjacent grounded ice and vertical stresses. Reference Jacobel and BindschadlerJacobel and Bindschadler (1993) calculated that the vertical shear exerted on the ice in a similar situation on an Antarctic ice stream would require a few years to equilibrate to a hydrostatically balanced configuration.
Sub-ice-shelf bathymetry
Figure 1 shows tracks where Autosub collected the first measurements from within the ocean cavity beneath the PIG ice shelf (Reference JenkinsJenkins and others, 2010). They were intentionally positioned close to the 2004/05 flight tracks. The closest seabed elevations measured by Autosub are included in Figures 4–7. Interpreted collectively, these measurements show a large seabed ridge positioned approximately midway between the grounding line and the ice-shelf front, oriented roughly perpendicular to the ice-flow direction and extending from the northern margin southward at least as far as the southernmost track (Reference JenkinsJenkins and others, 2010; Fig. 1). The three northern cruises did not travel landward beyond the ridge crest, so the ridge’s maximum height in these areas remains unknown as does the shape of the bed landward of the ridge. In contrast, the longest track did clear the ridge to travel nearly to the grounding line of our profile 4 (Figs 1 and 7) to confirm that in this region the seabed is >1000 m below sea level.
There is a suggestion in profiles 2 and 3 that downstream of the ridge crest the ice bottom becomes smoother and the ice thickness more uniform. The passage of the ice seaward over this crest carries this undulated topography into a warmer-water regime on the seaward side of the ridge as measured by Autosub (Reference JenkinsJenkins and others, 2010). Any correlation is less clear in profile 1 because the actual location of the ridge crest is undetermined and, although profile 4 (Fig. 7) includes the complete ridge cross-section, the flight path and the flow direction diverge soon after passing the ridge crest which limits the confidence of possible connections between the ridge and the ice-bottom topography.
In front of the ice shelf, shipborne swath bathymetric data were collected, indicating fine-scale lineations aligned with the ice-flow direction overprinting the previously known gross-scale bathymetry. On this large scale, there is a deeper channel (∼1000 m deep) entering beneath the southern half of the ice-shelf front, while on the northern half, the seabed is shallower, rising from about 800 m depth at the edge of the south channel to 400 m depth at the north edge of the ice-shelf front (Reference Jacobs, Hellmer and JenkinsJacobs and others, 1996).
Inversion of airborne gravity collected in 2009–10 as part of NASA’s IceBridge mission has added coarse bathymetric information in areas not sampled by Autosub (personal communication from M. Studinger, 2010). Although inversion of these data has not yet been entirely reconciled with Autosub data in some critical locations, the bathymetry inverted from the gravity data suggests a channel exists to the south of the ridge, the possible existence of which might allow deep water to access the deep cavity landward of the ridge and adjacent to the grounding line.
Ice-shelf thickness and ocean heat
IHere we examine the spatial variability of the ice thickness along profile 4 presented above and compare it with modeled variability in ocean conditions of the Amundsen Sea. The quasi-regular spacing of the ice-thickness variations is quantified by measuring the distance between successive keels beginning with the prominent keel at km 33 and ending near km 70. The mean spacing is 2480 km, with 3300 and 1600 km being the maximum and minimum spacings, respectively. The mean value is close to the average annual movement of the ice shelf prior to its recent acceleration (Reference Joughin, Rignot, Rosanova, Lucchitta and BohlanderJoughin and others, 2003). Figure 8 compares published speeds for various dates (Reference Joughin, Rignot, Rosanova, Lucchitta and BohlanderJoughin and others, 2003; Reference RignotRignot, 2008) with the inferred annual speed of the ice shelf between keels assuming the keel at km 33 was formed in 2001. The agreement displayed in Figure 8 is sufficient to establish that these ice-thickness features are formed on a roughly annual basis.

Fig. 8. Plot of surface velocity across the grounding line of PIG from Reference Joughin, Smith and HollandJoughin (2003) (green triangles) and Reference RignotRignot (1998) (purple crosses) compared with speed assuming keels of ice shelf along south profile (see Fig. 7) are produced annually (blue diamonds).
The appearance and periodicity of the surface undulations is reminiscent of ogives on glaciers, suggesting they might be formed by a similar process. Ogives form by seasonal changes in ice flow. However, quasi-annual variations in the ice flow as a formation process here can be discounted for two reasons: (1) velocity variations of this type have yet to be reported despite studies of year-round ice flow at several sites on the glacier (Reference Scott, Gudmundsson, Smith, Bingham, Pritchard and VaughanScott and others, 2009); and (2) since horizontal velocity is constant with depth, the resulting ice-thickness variations would be evident on both the surface and bed topographies simultaneously, contrary to the above discussion of subdued surface undulations immediately downstream of the grounding line. Thus, we continue to analyze our contention that these ice-thickness variations form by temporally variable basal melting of the ice shelf at the grounding line followed by eventual downstream hydrostatic equilibration.
The temporal variability of heat contained in waters of the Amundsen Sea, including beneath the PIG ice shelf, was modeled by Reference Thoma, Jenkins, Holland and JacobsThoma and others (2008). Those authors calculated the oceanic circulation throughout the Amundsen Sea and the adjacent deep Southern Ocean by forcing an 11-isopycnal-layer ocean model with daily mean surface air temperatures and sea-level pressure from the US National Centers for Environmental Prediction/US National Center for Atmospheric Research (NCEP/NCAR) reanalysis product for 25 years (1980–2004). There were few direct observations to gauge the accuracy of these model results, but the authors concluded from sensitivity studies with the model that the variability of the heat offshore of PIG is a robust result and a direct consequence of the time-varying wind-forced ocean circulation.
In our analysis, we use their model output of the heat contained within a 24-gridcell volume in the southeastern region of the Amundsen Sea, centered ∼110 km from the front of the PIG ice shelf (box ‘c’ in fig. 1 of Reference Thoma, Jenkins, Holland and JacobsThoma and others, 2008). The heat content within this volume is dominated by the heat within the deep layers composed of the shallower of the two CDW layers (their layers 7 and 8) and the next most shallow layer (their layer 6). The timing of the annual heat maximum in this box is highly variable (see fig. 3d of Reference Thoma, Jenkins, Holland and JacobsThoma and others, 2008): during the interval 1980–93, it occurs in late austral summer (February–April); however, from 1994 to 2004, winter maxima are more common. This may represent a shift in a large-scale climate oscillation reflected in the winds that force the upwelling of warm CDW onto the continental shelf. The timing of the annual minimum in the ocean heat is slightly more regular, occurring most often in July (austral midwinter). The strength of both maxima and minima is also highly variable. The summer to winter variation in total heat can exceed 100% in some years, with the seasonal variation in heat for the CDW contribution even larger.
To compare Reference Thoma, Jenkins, Holland and JacobsThoma and others’ (2008) monthly time series of heat in the southeastern Amundsen Sea with our data of ice-thickness variations along profile 4, we produce a time axis along the profile by calculating the downstream distance traveled along this profile by ice passing the grounding line in each month of the dataset of Reference Thoma, Jenkins, Holland and JacobsThoma and others (2008). The relationship is
where X is the longitudinal position, with X 0 being the grounding-line position (km 22.4), T is the time of a particular heat value, with T2005 being the beginning of calendar year 2005 (the date of the airborne profile measurements), V(t) is the velocity of the ice at the grounding line and t is time. A constant position of the grounding line is assumed because of the complexity and orientation of the transition in this region and because a complete record of grounding-line position is not available (see Fig. 1). However, a temporally variable velocity is applied according to a fit of the published data included in Figure 8. These velocities apply only to the grounding-line region, not downstream, so longitudinal strain rates extracted from the velocity field measured in 2006 (personal communication from E. Reference RignotRignot, 2008) are also applied to account for downstream stretching after the ice passed the grounding line using
where ΔX is the extra downstream distance due to longitudinal strain experienced by ice at position X, ε xx is the longitudinal strain rate along the profile, and the integration is from the grounding line to position X. The additional displacements caused by longitudinal stretching are modest as longitudinal strain rates along profile 4 have a mean value of 0.005 a−1. Equation (2) was evaluated for each month spanning the dataset of Reference Thoma, Jenkins, Holland and JacobsThoma and others (2008) to obtain a rough estimate of the ice-shelf position (its X position) and then Equation (3) was applied to displace the ice associated with each month farther downstream (the ΔX value). The corresponding monthly heat values were then tied to the positions of the associated ice.
Figure 9 presents the comparison of heat in the ocean box with the thickness variations along profile 4. There is a very close correspondence between heat variation and ice thickness over the upstream (most recent) half of the heat record. During these years (1994–2004) the heat record is characterized by sustained higher-than-average annual heat values interspersed with pulses of much warmer water. To facilitate a statistical comparison, ice thicknesses over the interval from km 22 to km 54 are detrended in Figure 9b using a five-term polynomial approximation to the local mean ice thickness. Periods of warmer-than-average water correspond to the thinnest sections of the ice shelf with a statistical correlation coefficient, r 2, of 0.65.
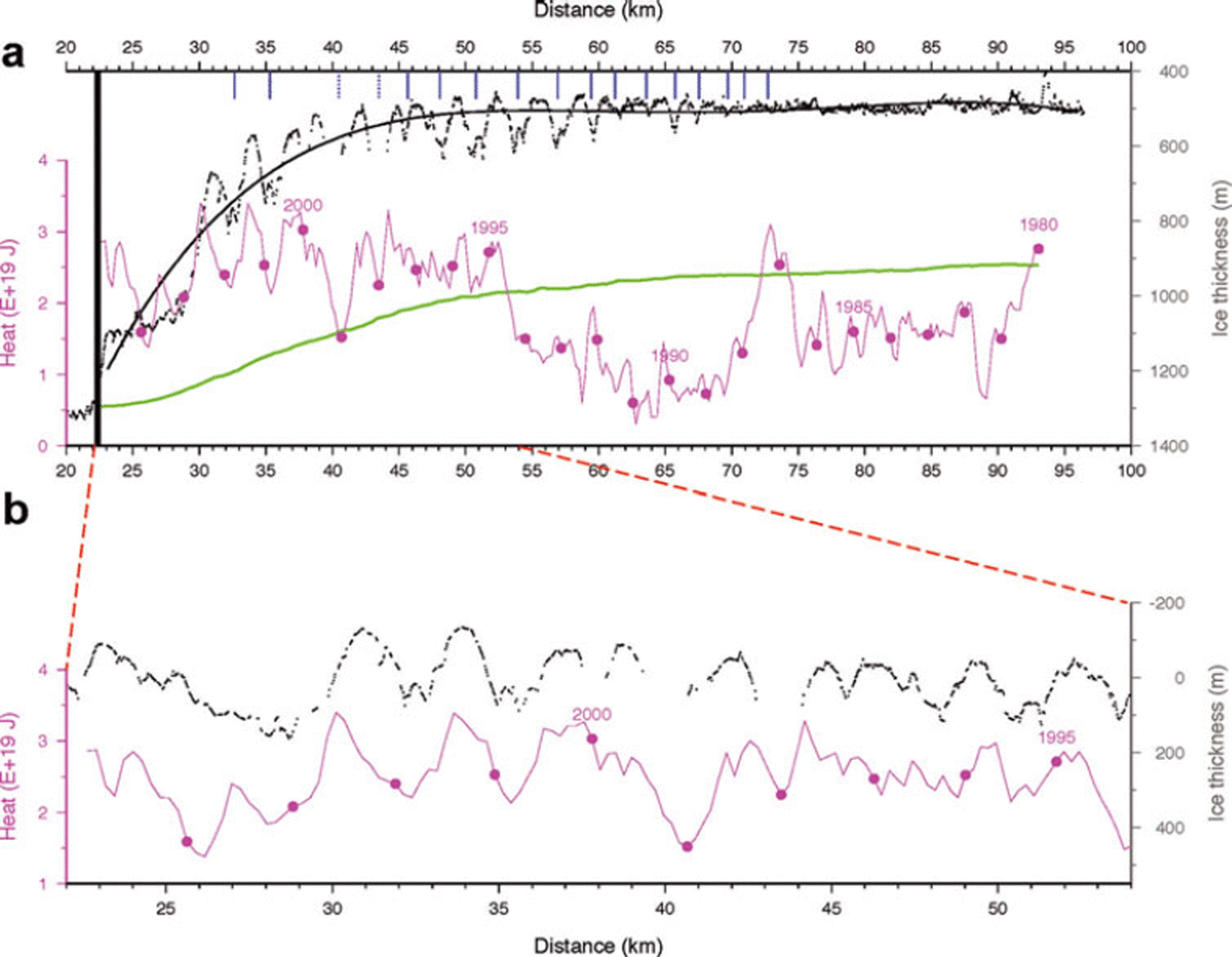
Fig. 9. (a) Black points are measured ice thicknesses along profile 4 (Figs 1 and 7) and the curve is a five-term polynomial fitted to these data. Heavy black vertical line indicates the grounding-line position used for calculations. Blue vertical lines indicate the crest locations of surface undulations. Magenta curve is the monthly values of total ocean heat in the gridcell immediately in front of the PIG ice shelf mapped to positions along the ice shelf as described in the text; dots correspond to January of each year. Green curve is the ‘no melt’ ice bottom calculated from observed surface velocities and strain rates as described in the text. (b) Expanded section of profile including ice thickness and ice-front ocean heat values where the ice-thickness values have been subtracted from the fitted polynomial surface to show the similarity between these two series.
The heat record prior to 1994 is generally much cooler (including a shift in the timing of the annual heat maximum), so these values were not included in the correlation calculations. Nevertheless, the variability of the two parameters seems to continue, with peaks in both heat content and ice thickness at km 60 and km 65. Downstream of km 70, the flight-line veers away from the surface waves, preventing examination of possible correlations during the period of cooler ocean conditions, including the 18 month long pulse of very warm water in 1987. Even so, it is surprising that there is no signature of thinner ice in the imagery (Fig. 1), for example a broad surface trough.
Returning to Figure 9b, there are small horizontal offsets between the heat pulses and the thinner ice-shelf areas. We consider these offsets as indicative of the time it takes water to travel from the center of the ocean box to the grounding line, a distance of ∼170 km. The ice keels and corresponding heat minima provide the most reliable measurement of this delay. When converted to time delays, the spatial offsets between the relative heat minima and the associated keels exhibit a large scatter with a mean value of 1.15 ± 1.7 months. It has been noted that the model also produced highly variable currents within the box we consider here (personal communication from A. Jenkins, 2011). This mean delay corresponds to a mean ocean current of 5.6 cm s−1. Considering the broad assumptions that are involved, this value is remarkably close to an inflow current of 4.3 cm s−1 derived from ocean measurements made directly in front of the ice shelf in 1994 (Reference Jacobs, Hellmer and JenkinsJacobs and others, 1996).
Basal melting rates
Having tied the record of ocean heat to melt features on the ice-shelf underside, we explore their quantitative relationship. First, we consider the excess heat contained in the quasi-annual warm water pulses and the additional ice melted in the thinner voids of the ice shelf, presumably by this excess heat. The heat contained in these warmer pulses is quantified by integrating the additional heat above a base level defined by the coolest periods on either side of each warm pulse as illustrated in Figure 10a. This represents a minimal case, but the results of defining other base levels do not significantly alter the overall conclusions drawn below. The average magnitude of each heat pulse is calculated by dividing the time integral of heat in each pulse (above its base level) by the duration of each pulse. The corresponding losses of ice are quantified in a similar manner, defining pulses based on the ice-thickness values using base levels drawn between keels (minimum ice loss) and calculating the loss as the average magnitude of ice lost between the base level and the ice bottom across each void (Fig. 10b). The actual values of these calculations are given in Table 1. The duration of each pulse is not precisely 1 year (the actual durations are also included in Table 1), but we regard them as annually averaged amounts for some of our analysis.
Table 1. Calculated characteristics of heat pulses and ice voids from Figure 10


Fig. 10. Profiles of (a) time-varying heat and (b) ice-thickness variations versus along-profile distance. Red-line segments near 40 and 43 km depict estimates used to fill gaps in ice-thickness data. Heat pulses and corresponding ice-loss voids are defined as discussed in the text and paired by number. The pulse magnitudes of excess heat or excess ice loss are calculated by integration of the pulse area above the base levels defined by the blue lines drawn between local minima. Magnitudes of total heat and ice loss are calculated as the total area between each curve and a base of zero (for heat) or the ‘no melt’ base (for ice loss).
Before considering this relationship, we recall that radar reflection hyperbolae from deeply incised bottom crevasses may lead to an overestimate of ice loss. For this reason, the hydrostatically equilibrated ice bottom, calculated from the measured surface elevations and Equation (1) (cf. Fig. 7), is used in a similar manner to the measured ice thickness and, by using the same method described above, a second set of ice-loss values is obtained. Excess heat values remain unchanged. No values for the voids inferred from the hydrostatic ice bottom are included for the first three pulses because they are underestimated due to the delay in forming a strong surface elevation expression of basal ice loss, as discussed earlier.
The values of excess heat and ice loss for each pulse and void are plotted in Figure 11. There is considerable scatter, but generally the warmer the pulse in the ocean box, the more ice is lost. The mean values are (0.44 × 1019) ± (0.18 × 1019) J and 73.6 ± 25.1 m. Because there is uncertainty whether basal crevasses mask the true ice bottom, Figure 11 also includes an additional set of points using ice void sizes derived from the hydrostatically equilibrated ice bottom that was computed using Equation (1). Even though the ice void sizes change, the overall pattern is not significantly changed. Ice voids 1–3 are omitted from this second set of points because the hydrostatic ice bottom is probably an unreliable representation of the true ice bottom.
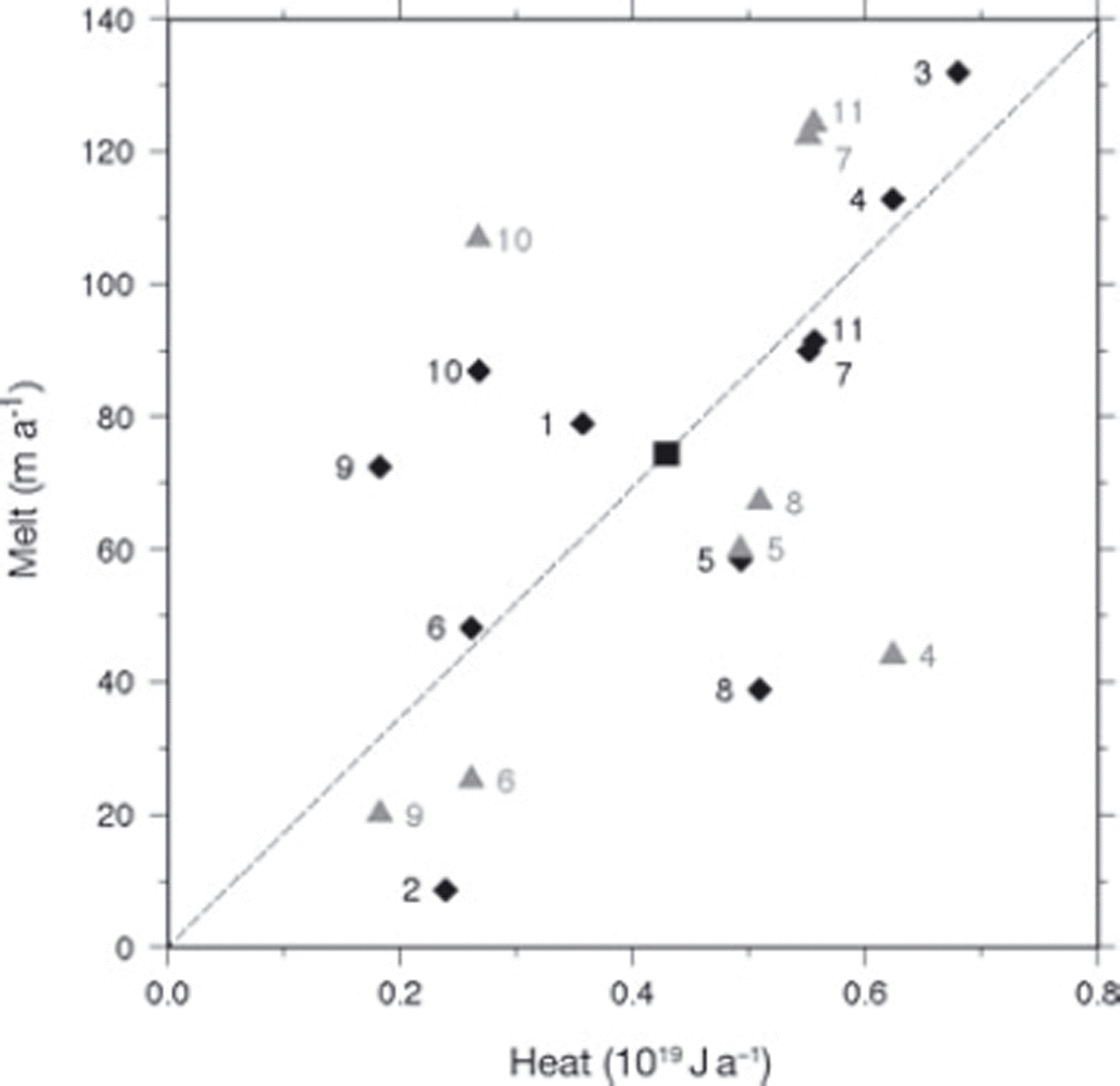
Fig. 11. Time-integrated heat and ice melt for each pulse identified in Figure 10 along profile 4 from 1994 to 2003. Heat values correspond to the sensible heat contained in the ocean box in the southeastern Amundsen Sea (not the heat under the ice shelf). Ice melt is calculated from either the measured ice thickness (black diamonds, with the mean values at the location of the black square) or the hydrostatically equilibrated ice thickness (grey triangles) as discussed in the text. Numbered labels correspond to the pulse interval (cf. Fig. 10).
The average ice volume lost in one of the voids created by a pulse of excess heat can be estimated by taking the product of the axial length of a typical void (estimated as 10 km from Fig. 1), the mean spacing of 2.48 km between voids and 74 m mean height of the voids (from Fig. 11). The result is an average melt volume of 1.835 km3; this can be considered an annual average.
We introduce one additional theoretical ice bottom, one that represents where the bottom would be if there was no basal melting. The ‘no melt’ ice-thickness profile is calculated by converting the surface-parallel strain rates (both longitudinal, which dominate, and transverse) from the 2006 velocity field (personal communication from Reference RignotE. Rignot, 2008) to vertical strain rates and applying these to the measured ice thickness at the grounding line as the ice moves downstream. The equation used is
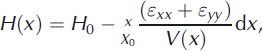
where H 0 is the ice thickness of the grounding line at position X 0, ε xx and ε yy are the longitudinal and transverse strain rates, respectively, and V(x) is the ice velocity. The ‘no-melt’ ice thickness allows us to quantify the melt caused by the sustained input of heat, i.e. total heat minus the heat of the quasi-annual heat pulses. This is illustrated in Figure 10 as the distance between the ‘no melt’ ice thickness and the base levels beneath the quasi-annual ice voids. These values are included in Table 1 as ‘non-seasonal ice melt’ for each quasi-annual pulse.
‘No melt’ profiles of ice thickness were calculated for each of the four profiles as described above, and the ice lost at selected points along each profile was computed by differencing these ‘no melt’ profiles from polynomials fit to the measured ice thicknesses (Fig. 12). Depending on the complexity of the ice-thickness profile, five-, six- or seven-term polynomials were used. Figure 12b shows that significant melt occurs along the underside of the ice shelf, as first estimated by Reference Jacobs, Hellmer and JenkinsJacobs and others (1996) and later supported by others (Reference RignotRignot, 1998; Reference Rignot and JacobsRignot and Jacobs, 2002; Reference Payne, Holland, Shepherd, Rutt, Jenkins and JoughinPayne and others, 2007; Reference Joughin, Smith and HollandJoughin and others, 2010), but that the pattern of melt varies enormously between profiles.

Fig. 12. (a) Calculations of non-seasonal ice melt along each profile (1, gray; 2, blue; 3, green; 4, red) derived as difference between polynomial fit (thin black curve) to measured ice thickness and ‘no melt’ ice bottom (thick black curve) calculated from grounding-line ice thickness and thinned downstream according to local strain rates as described in the text. (b) Ice lost vs downstream distance from the grounding line (primary axis) and date on which ice passed the grounding line (secondary axis). Larger dots indicate extent of near-grounding-line region discussed in the text and included in Table 2.
Small transverse velocity gradients between the profiles allow the inclusion of a secondary time axis in Figure 12 to indicate the time that the ice at the position transited the grounding line. This time axis permits the interpretation of the slope of the plotted profiles of ice lost as estimates of the basal melt rate. Profiles 2 and 3 show a similar pattern of decreasing basal melt rate downstream. Profile 4 displays a higher melt rate at the grounding line, but the trend of this curve changes sign downstream, suggesting basal freezing. This is likely spurious, the result of the deep keels along this profile (cf. Fig. 10). Profile 1 is distinctly different, with negligible melt occurring over the first 30 km downstream of the grounding line before the melt rate gradually increases.
Figure 12 is used to calculate two estimates of nonseasonal melt flux. The values are presented in Table 2. The first estimate extends over most of the ice shelf. Equal weighting applied to each profile produces an estimated basal melt flux of 44.2 km3 a−1 (40.5 Gt a−1). The second estimate applies nearer the grounding line; however, the downstream limit of this zone is rather arbitrary for some of the profiles. The mean longitudinal length of this region is only 24.3 km, compared with 61.5 km for the nearly full profile estimate, but the estimated basal flux is 42.8 km3 a−1 (39.2 Gt a−1). These basal melt fluxes compare favorably with the net melting of 40 Gt a−1 calculated by Reference Joughin, Smith and HollandJoughin and others (2010). In fact, these may be slight underestimates because the ice shelf has been measured to be thinning by a few meters per year (Reference Shepherd, Wingham and MansleyShepherd and others, 2002; Reference ThomasThomas and others, 2004), but the error is relatively small given the magnitude of melt. It is also consistent with the view that basal melt is more intense near the grounding line (>150 m a−1 for profile 4), but shows melt continuing, albeit at more modest rates, downstream.
Table 2. Calculation of ice-shelf-wide and near-grounding-line basal melt flux for each profile

Next we compare the amount of heat required to melt these annual volumes of ice to the heat arriving at these locations using
where Q is the heat, ρ i is the density of ice (917 kg m−3), L is the heat of fusion for ice (333.55 kJ kg−1) and F is the volume of ice. The oceanic heat values provided so far are for a region 110 km from the ice shelf. Reference Thoma, Jenkins, Holland and JacobsThoma and others (2008) did calculate basal melt rates and residual heat beneath the ice shelf, but the melt rates were too small and the residual heat alone does not provide a means to estimate the incoming heat flux. Instead, we turn to field data collected across the ice-shelf front in 1994 by Reference Jacobs, Hellmer and JenkinsJacobs and others (1996), who calculated a 0.172 Sv transport into the sub-shelf cavity over a depth range of 800–1000 m, the deepest 20% of the water column. The correlation of the temporal variability of the heat content in the ocean box with the wave structures on the ice shelf (cf. Fig. 9b) leads us to assume that the heat structure and content of the ocean box are similar to those of the water that enters the PIG cavity. This box has an area of 5400 km2 and a maximum depth of 810 m. We further assume that the heat that does enter the cavity comes from the deepest 20% of the box (a depth range from 650 to 810 m). This depth range contains approximately half of the heat within the box. Based on these estimates, the annual flux of heat into the PIG cavity is roughly three times the heat content of the ocean box. As a check on some of these estimates, we calculate that when the heat content of the ocean box is a typical value of 2 × 1019 J, the average temperature of the layer occupying the lowest 20% of the box is 2.7°C, a reasonable value for CDW (Reference Jacobs, Hellmer and JenkinsJacobs and others, 1996).
Given these values, we can estimate the efficiency of the pulse melting process and of the more broadly distributed basal melting downstream of the grounding line. From the preceding discussion, the mean annual excess heat that actually flows beneath the ice shelf to form the pulses is 1.32 × 1019 J, three times the mean heat value in Figure 11. From Equation (5), the heat required to melt the average void volume of 1.835 km3 is 0.051 × 1019 J. This implies a melt efficiency of only 4%. By comparison, melting across the entire ice shelf occurs at an annual rate of 44.2 km3 a−1 requiring 1.35 × 1019 J a−1. By taking the average heat content in the ocean box, 2.04 × 1019 J, the annual amount of heat entering the cavity is 6.12 × 1019 J for a melting efficiency of 22%.
These estimates are admittedly rough, but they confirm the assessment by Reference Jacobs, Hellmer and JenkinsJacobs and others (1996) that there should be considerable residual heat in the water exiting the subice-shelf cavity and returning to the ocean. They also suggest that there is sufficient heat for additional melting.
Polynyas close to the ice-shelf front
The circulation of water beneath an ice shelf includes exiting currents that are generally shallower than incoming currents due to decreased salinity resulting from basal melting (Reference Jacobs, Hellmer, Doake, Jenkins and FrolichJacobs and others, 1992). This water is often observed to remain below the surface, returning to the open ocean at intermediate depths. Measurements in front of the PIG ice shelf identified exiting water from 300 to 800 m depth flowing at 2.0 cm s−1 (Reference Jacobs, Hellmer and JenkinsJacobs and others, 1996).
Satellite images of the PIG ice shelf frequently show the presence of polynyas, regions of open water surrounded by sea ice, at the ice-shelf front (Fig. 13); however, there are also summers when there is no sea ice at the ice-shelf front. The presence of sea ice and polynyas in front of the ice shelf is captured on satellite images. A review of all Landsat imagery available for the ice front of the PIG ice shelf produced 116 useful acquisitions (low-resolution browse images of 180 or 240 m resolution were sufficient for this purpose) spanning 35 years. To make the satellite observational record as complete as possible, seven additional images from the Advanced Very High Resolution Radiometer (AVHRR) and Moderate Resolution Imaging Spectroradiometer (MODIS) were also used, although the lower resolution of these sensors (250 m for MODIS, 1 km for AVHRR) sometimes made it difficult to identify polynyas.

Fig. 13. (a) Annotated subset of figure 4 from Reference Payne, Holland, Shepherd, Rutt, Jenkins and JoughinPayne and others (2007) showing predicted water circulation vectors beneath the PIG ice shelf. Red lines are added to indicate shear margin of ice shelf, and red letters mark locations of the three persistent polynyas. (b) Subset of Landsat-7 image collected on 24 January 2005 showing the locations of the three persistent polynyas. Orientation is identical to Figure 1.
We observe in this record that when polynyas are present there are usually three, they persist throughout the summer and their locations do not change (Table 3). Polynyas were not observed in any other locations. The largest polynya is usually positioned at the extreme southern end of the ice-shelf front, another is located approximately halfway across the ice front and the third is at the northern extreme of the rapidly moving ice front (Fig. 13). Notably, these locations are precisely those predicted for exiting water by a plume model of sub-shelf circulation, with the southern exit being the most vigorous (fig. 4 of Reference Payne, Holland, Shepherd, Rutt, Jenkins and JoughinPayne and others, 2007; Fig. 13). This result may be serendipitous because the plume model is a ‘reduced gravity’ model in which bathymetry beneath the ice shelf plays no role, although it did include an approximation of the measured bathymetry across the ice-shelf front, including the deep channel spanning the southern half of the ice front (Reference Jacobs, Hellmer and JenkinsJacobs and others, 1996).
Table 3. Observations of ice-front conditions from satellite imagery. Results are expressed as a ratio between the number of occurrences and the number of times the location was within the image field of view

The middle polynya exists at the end of a significant longitudinal surface trough, visible in Figure 1. Previous discussion has established that the majority of the ice shelf is in hydrostatic equilibrium, so this surface trough is likely underlain by a deep inverted trough in the underside of the ice shelf. Such a trough would confine and channel buoyant water rising along the ice-shelf underside. Establishing that the locations of polynyas match the predicted locations of exiting sub-shelf water carries with it two major implications: (1) the exiting water probably carries residual heat, thus melting the sea ice, creating the polynyas and maintaining them through the summer; and (2) the exiting water has sufficient buoyancy to rise the final 270 m from beneath the ice shelf to the surface. Rather than forming polynyas by melting, it is also possible that they are caused by horizontal divergence of rising water once it reaches the surface. We favor melting as the primary process because the highest-resolution imagery shows neither signs of rafted sea ice around the polynya nor a lead pattern that would suggest a local divergence of the sea-ice cover away from the polynyas.
The temporal characteristics of the satellite record are summarized in Table 3. Data are too sparse during the first third of the record (1970s through mid-1980s) to suggest a preferred state. During the middle third of the record (the 11 years beginning in 1986/87) open-ocean conditions were far more prevalent (9 out of 11 years) than sea ice against the front. A marked reversal in this tendency is evident over the last 9 years, with sea ice and polynyas occurring in 7 of the 9 years. 2007/08 was an unusual year when there was a large rift extending across the ice shelf at the beginning of the summer. The middle polynya was never observed during this season and, once the iceberg drifted away, no sea ice formed at the new ice front. It is likely that the rift disturbed the exiting flow of water which otherwise would have formed the middle polynya.
Landsat thermal band data provide an additional means of exploring our interpretation that the sub-ice-shelf waters rise to the surface in these three specific locations even in those years when there is no sea ice against the front and isolated polynyas cannot be observed. Of the 13 known years with a sea-ice-free ice front (cf. Table 3), multiple 60 m resolution Landsat thermal band images were collected twice (during the 2002/03 and 2008/09 austral summers). Figure 14 shows a temporal series of the 2002/03 thermal data, enhanced to show only the thermal range just above the freezing point of sea water (approximately −2°C). The thermal band data record only the skin temperature of the water, probably within the uppermost millimeter of water. In the two earliest images, the warmest waters occur next to the ice-shelf front. In particular, the image from 16 November 2002 shows three warm spots at the same locations where polynyas form in years of heavier sea ice.

Fig. 14. Landsat Enhanced Thermal Mapper Plus (ETM+) thermal band images of the front of the PIG ice shelf collected on the dates indicated. Colored regions are the open-ocean surface; all ice surfaces are black and the images are oriented as in Figure 1. The ice shelf is at the top and an irregularly shaped iceberg appears at various orientations in some of the images. White arrows indicate positions of warmer-water plumes exiting the ice-shelf front where polynyas often appear.
The recorded surface water in these locations is no more than 1°C warmer than the surrounding water. The precision of the Landsat thermal band temperatures is about 0.5°C. It is possible that the rising water is warmer than the temperature recorded at the surface, but this cannot be confirmed with these data. As the summer progresses into late December, the surface waters warm and other circulation patterns dominate the surface water temperature field. It is possible that the years with no sea-ice cover represent unusually large amounts of exiting warm water, essentially merging the individual polynyas into a single polynya extending across the entire ice-shelf front. At the end of the summer, as the skin cools again, the March 2003 image hints at warmer exiting water reappearing. We regard these thermal data as strong evidence that even in years without sea ice, warmer water is exiting from beneath the ice shelf in the same locations where individual polynyas appear in other years. Thus, it is likely that, irrespective of the local sea-ice conditions, some water exiting beneath the PIG ice shelf remains buoyant enough and warm enough to rise to the surface with enough heat to maintain local polynyas.
Discussion and Summary
The combination of satellite imagery and airborne surface-elevation and ice-thickness measurements provides a new opportunity to investigate the interaction of the ocean with the PIG ice shelf. Matching the detailed position and shape of the set of undulations along the southern ice shelf with the temporal variability of heat in the southeastern Amundsen Sea demonstrates that the variability of atmospheric winds in this region is directly imprinted on the ice shelf through the formation of quasi-annual ice-thickness variations that are then seen as waves in the surface topography. Additionally, quite apart from their clear connection to atmospheric behavior via the ocean, a number of other issues require explanation: how do these waves actually form? why do they occur where they do? and why don’t they occur elsewhere? We address each of these in turn.
The formation of the undulations involves both pulses of warmer-than-average water and basal crevasses. It is unlikely that the formation of the basal crevasses at the grounding line is synchronized with the arrival of the warm-water pulses without some cause-and-effect connection. We suggest they are connected through grounding-line dynamics. Either there are many basal crevasses being formed throughout any year and the warm water happens to act on the one closest to the grounding line, or the arrival of the warm water acts to initiate a basal crevasse. The former explanation is unlikely because there is always heat entering the ice shelf and, presumably, reaching the grounding line. Thus every basal crevasse would be injected with warm water as it formed, although some would be injected with warmer-than-average water, so we would expect more frequently spaced ice voids to be produced than are observed. The latter explanation requires not only higher melt rates and grounding-line retreat at the grounding line, but a dynamic response of the ice there. One possibility is that the ice-flow acceleration is sufficient to cause a local crevasse to form through the increase in longitudinal extension. An alternative explanation is that the longitudinal extension increases because the longitudinal stress is supported by a thinner ice shelf. In either case, it suggests an even more active linkage between the interaction of the ocean and the dynamics of the ice sheet at the grounding line.
The downstream preservation of the pattern of ice void shapes and spacing allows it to be matched to the temporal variability of the ocean heat. Preservation also means that the void shapes are not strongly altered by later-arriving water. Although we estimate that the overall melt efficiency of the heat pulse is only 4%, the melting caused by the fraction of the water present at the grounding line that actually enters the crevasse as it forms is probably much higher. The large surface area of the new crevasse would provide an extensive interface for heat exchange. On the other hand, the narrow shape of the void would restrict water circulation within the void, and the exposure within the crevasse to ice at temperatures lower than the pressure-melting temperature would conduct heat from the water to warm this ice without melting. Nevertheless, if exchange with water outside the void is severely restricted, eventually all the heat of the water within the void must be lost to the ice. As melt proceeds, the difference in density between ice and water would require that some external water would enter the basal crevasse. We can speculate on the details of this process but we have few data that would allow us to decide the relative importance of competing processes. Figure 7 hints that the first two voids, up to km29, are not as completely formed as all the remaining voids, so there is a hint that void geometry evolves to some degree. Basal slopes along the sides of the undulations are often 10° and sometimes even steeper, so the isolation of water trapped in the ice voids is possible.
The most satisfactory explanation of why the undulations form where they do appears to be the presence of the seabed ridge which may mean that the deep incoming water passes to the south of the ridge, causing it to access the grounding line first near the south end. The airborne gravity-based bathymetry has not yet been reconciled with the Autosub bathymetry, but the southern limit of Autosub data indicates a downward-dipping end to the ridge. The orientation of the undulation axes is parallel to the grounding line (Fig. 1). This also is an area where the grounding line has been relatively stable since 1992 (Fig. 1). This could explain why this series of features extends the full length of the ice shelf, indicating persistent broad-scale sub-ice-shelf oceanographic conditions throughout the last 25 years.
More difficult to explain is why the waves form in such a laterally limited area if only 4% of the available heat is expended in their formation. Details of the circulation pattern are probably involved. Coriolis forces steer moving water to the left. This effect would make it difficult for water that entered near the southern end of the grounding line to proceed northward around the prominent peninsula of grounded ice extending farther downstream over the central portion of the ice shelf. Instead, the incoming water, made lighter through a decrease in salinity, would hug the southern shore as it exited the cavity. The voids might play a role in steering the exiting water in this southward direction.
Perhaps significantly, between 2000 and 2009, grounding-line retreat separates this grounded peninsula of ice from the glacier, creating a more direct pathway for water to reach the north side of the grounding line (cf. Fig. 1). It is during this transition period that a new set of waves is seen to form on the north side of the grounding line (Fig. 2). We cannot be certain that these waves are akin to the waves on the south side, but it is a reasonable assumption. Their orientation is angled in the opposite direction to the southern set and may be an expression of the grounding-line orientation or reflect the principal axis of tension (and resulting basal crevasse orientations) for side shear of the ice shelf against the nearly stagnant adjacent ice. We expect they are similar in morphology and form in a similar manner to the south set of waves, i.e. the pulse of warmer water causes higher melt rates, lower friction, sudden acceleration and, ultimately, formation of a basal crevasse into which the warmer water flows, melting an ice void. We cannot be sure that this warmer water is arriving by the same path as in the south. They may appear due to a change in the stress state at the grounding line of profile 1; however, the more intermittent occurrence of flow-transverse ridges and troughs in the central ice shelf between these two sets of waves may hint at exactly this type of revised circulation pattern (Fig. 3). A lack of these flow-transverse features downstream, in ice passing the grounding line earlier than this transition, supports our view.
A variety of grounding-line conditions is emphasized by the variety of basal melt patterns for the four profiles (Fig. 12). Profile 1 is most unlike the others. Its constant thickness (cf. Fig. 4) suggests very little basal melting, while the thinner downstream reach and the high slope of its melt profile in Figure 12 suggests the opposite may have been true a decade earlier. The visual evidence also indicates this region has undergone considerable change with the shift from a relatively smooth surface over the thinner downstream section, to a highly crevassed surface upstream (i.e. more recently) with the most recent addition of a set of surface waves possibly associated with the breaching of the grounded peninsula.
Profiles 2 and 3 are more typical in their patterns of basal melt, despite the fact that they are atypical in remaining near grounded ice for a much longer time than ice along the other profiles (Fig. 2). Profile 4 has the highest basal melt rate, but it persists for the shortest time. The melt rates do suggest a northward decrease consistent with, but not confirming, a southern entry of incoming warm water.
Overall, the 22% melt-rate efficiency is much higher than the efficiency of the melting associated with the waves. Nevertheless, the volumes of the ice voids are sufficiently small that most of the water carrying the additional heat during the warmer pulses is not trapped in the voids. We have discussed these two components of the incoming heat separately, but the ice shelf experiences no difference between them. The pulse heat has an average annual value of 0.44 × 1019 J. Assigning most of this to water that is not sequestered in the voids increases the heat available for melt across the ice-shelf base to 2.48 × 1019 J and reduces this overall efficiency to 18%.
Our observation of what appears to be exiting water at the surface adjacent to the ice front is consistent with our conclusions of sub-shelf processes. Sub-shelf melting all the way to the ice front appears likely along two of the profiles; however, it is also very likely given the nature of the surface topography that most of this water is confined within troughs running longitudinally along the underside of the ice shelf. Such troughs have been detected by other aerogeophysical flights oriented transverse to the profiles discussed in this paper. They would concentrate the meltwater, freshening only the water contained within the associated ice-bottom void, allowing it to become lighter than the average exiting water. It is possible that there are two components to the exiting water: (1) the traditionally held intermediate meltwater plume that achieves neutral buoyancy before reaching the sea surface, losing contact with the ice-shelf base; and (2) channeled water that continues to freshen through melting basal ice along the entire ice-shelf underside until it reaches the ice front. While both components have been observed, through ocean measurements in one case (e.g. Reference Jacobs, Hellmer and JenkinsJacobs and others, 1996) and inferred from imagery in the other, present data are not sufficient to estimate their relative flux magnitudes.
Acknowledgements
Special thanks to B. Thomas who, to our knowledge, was the first to identify the quasi-annual character of the interesting waves on the south profile. A. Jenkins kindly provided the detailed model results from the ocean-modeling work of Reference Thoma, Jenkins, Holland and JacobsThoma and others (2008). Detailed and constructive reviews of an early manuscript were provided by I. Joughin, M. Thoma and A. Jenkins. Funding for the research came from NASA grant No. 509496.02.08.01.68 and US National Science Foundation (NSF) Office of Polar Programs (OPP) grant No. 0732906.