I. Introduction
The method commonly used in the past to determine the annual accumulation of snow in a permanent snow field, such as the Greenland Ice Sheet, has been by a direct examination of the stratification of the firn as revealed in pits. The properties of the firn which are usually determined are the density, the grain size, the crystal form and the degree of compaction, but normally the annual layering can be distinguished from the density profile alone.
A party of the British North Greenland Expedition, 1952–54, carried out a gravity survey across the northern part of the Greenland Ice Sheet, from Dronning Louise Land (lat. 77° N., long. 25° W.) to Nunatarssuaq (lat. 76° 30′ N., long. 68° W.), a distance of about 1200 km. The opportunity was taken to examine the firn structure at about 30 points on the route.
Although the direct examination of the firn gives information about properties other than the density, it is time-consuming, and the method adopted on this traverse was to make Rammsonde profiles to a depth of about three metres at each of the points.
The Rammsonde, a simple instrument developed by HaefelilReference Bader 1 , Reference Quervain 2 measures directly the “resistance to penetration” of the firn. It is the purpose of this paper to show that a direct relationship exists between the “resistance to penetration” and the density of a snow or firn layer, and that consequently an accurate density profile can be deduced from the “resistance” profile.
The experimental results used in this paper were obtained during the winter of 1953–54, at the Expedition’s central station, Northice (lat. 78° 04′ N., long. 38° 29′ W.), altitude 2345 m.
II. The Rammsonde Apparatus
The Rammsonde consists of a calibrated duralumin tube, 1 m. long, ending in a solid conical tip, the point of which is of hardened steel. The tube is of about 4 cm. diameter, the maximum diameter of the cone being about 5 cm. Two calibrated extension tubes, each 1 m. long, can be fixed end to end on the first tube by bayonet fittings, so that a total depth of 3 m. can be reached.
The upper end of the first, or of the uppermost extension tube, is sealed with a short plunger, to which is attached a calibrated rod, 60 cm. long. Cylindrical masses of 1, 2 and 3 kg. are provided, each with an axial hole so that the mass can slide freely on the rod.
The “resistance to penetration” of a snow layer is determined by measuring the penetration of the pointed tip when a weight is dropped vertically on to the flat upper surface of the plunger from a height measured on the calibrated rod.
If R is the “resistance to penetration” then the work done by the Rammsonde in penetrating a distance D cm. is equal to the loss of potential energy of the Rammsonde and weights.
Thus R (measured in kilograms) is defined by the equation
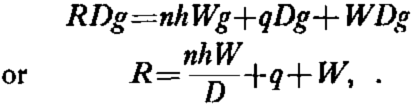
where n is the number of times the mass W kilograms must be dropped vertically from a height of h cm. to cause a penetration of the tip of D cm., and q is the mass in kIIograms of the tubes used. R, thus defined, has the dimensions of a mass and will be dependent on the geometrical form of the apparatus as well as on the properties of the firn layer.
In this equation small energy losses have been neglected. These include the elastic losses in dropping the mass and the friction between the tubes and the snow forming the sides of the hole. This second factor will be considered in the next section.
III. Corrections to the Measured Resistance for the Length of Tubing Used
Due to the frictional forces on the tubes the apparent resistance of a particular layer is greater when the layer is near the bottom of a three-metre profile than when it is close to the surface.
To determine the effect of the frictional forces on the measured resistance a series of overlapping Rammsonde profiles was made in the glaciological pit at Northice, which was eventually dug to a depth of 14 m. A three-metre profile was made, 2 m. of firn were dug away, another three-metre profile was made, and so on. Thus the resistance of a layer was measured first with 2 to 3 m. of Rammsonde tubing below the surface and then again with 2 m. less tubing, the difference in resistance being the frictional forces on the additional two metres. Unfortunately at depths greater than 8 m. the firn was so hard that it was impossible to pull out the Rammsonde after making a profile. Thus there are available only 4 profiles in which the overlap is sufficient to allow enough corresponding layers to be identified for a statistical analysis of the measured resistances. Frequently with high density layers (ρ > 0.52) it was not possible to penetrate the layer when it lay at a depth greater than 2 m.
In the upper layers, however, the correlation is high between values of R l+2, the apparent resistance of a layer initially at a depth of l+2 m, below the surface (0 < l < 1 m) and R l , the apparent resistance when the sounding is made after removal of the top 2 m. of firn. For the overlapping parts of profiles 1 and 2, 2 and 3, and 3 and 4, the correlation coefficients are all greater than 0.85, the number of corresponding layers being 15, 9 and 9 respectively. In these cases the mean density of the layer concerned is less than about 0.47.
If it is assumed that all of the energy losses are due to frictional resistance on the tube and the “resistance” of the layer at the tip of the Rammsonde, and further that the frictional resistance is proportional to the length of tubing (during a particular profile), then the difference
is equal to the frictional resistance on 2 m. of tubing; μ in the equation is the frictional resistance per metre of tubing and is not a constant, being dependent, probably, on grain size, density and temperature of the firn layers through which the Rammsonde has passed.
The three regression equations obtained for these overlapping regions are:

and
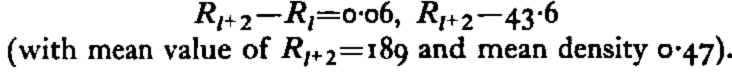
Thus the mean values of 2μ, as a percentage of the corresponding values of R l+2, are 19.6, 11.3 and 29%.
Corrections of this order of magnitude can be applied with some confidence, but at depths greater than 8 m. the correlations between R l + 2 and R l are much poorer (and are based on fewer pairs of observations), so that the corrections are correspondingly uncertain. With the harder layers it is also apparent that the loss of energy caused by the bouncing of the weight is large, and it seems to increase rapidly with the length of tube used.
Therefore it is unwise to use the resistances determined with more than 1 m. of Rammsonde tubing below ground, when the mean density of the 1 m. layer is greater than about 0.49.
With the same assumptions as given above one can write
where l is the length of tubing below the snow surface (0 < l < 3 m.), and μ is the resistance per metre, as before. Thus it should be possible to determine the true resistance of any layer. However, in the range for which it has been possible to determine p., the corrections to values of R l for values of l < 1 m., are of the order of 10% only. Since this is the order of magnitude of the accuracy of measurement of the penetration, this correction has not been made for values of l < 1 m. For l < 2 m., half of the correction given above has been applied. With Rammsonde profiles at greater depths, values of R l for l < 1 m. have been assumed to be correct, but values obtained with more than 1 m. of tubing have been ignored.
IV. Calibration of the Rammsonde
The densities of the firn samples used in the calibration of the apparatus were determined by weighing 500 cm.3 specimens extracted from the walls of pits in aluminium cylinders of about 28 sq. cm. cross-section. The cylinders were pushed horizontally into the walls. Samples were weighed with an accuracy of about 0.2 gm.
Because of the considerable size of the specimens required for the accurate determination of density, it has been possible in these studies to use only samples from regions where the “resistance to penetration”, and consequently the density, was sensibly constant over a vertical distance of 5 cm. or more.
The temperature of the firn in which the profile was made was not measured accurately. Near the melting point of ice variations in temperature may produce large variations in the “resistance to penetration” of a firn layer but, as with the other mechanical properties, at temperatures well below 0° C. the “resistance” is expected to vary only slowly with temperature. The temperature near the bottom of the 14 m. pit was approximately −28° C., and the temperatures of the fim layers at the time of the various soundings probably all lay in the range −22° C. to −32° C.
(a) Low density range
From the wall of a pit 3 m. deep 40 firn samples were taken. The mean density was 0.409, with standard deviation, σ ρ , of 0.056. A Rammsonde profile to a depth of 3 m, was taken at an adjacent point.
An inspection of the plot of “resistance to penetration” (measured in kilograms) against the density (measured in gm. cm.−3) of these 40 layers suggested that a direct relationship existed between the density of a layer and the logarithm of its resistance. Normal statistical treatment showed that the correlation coefficient, r, is 0.80, and the regression equation for density on log resistance (with the units given above, and assumed to be pure numbers), is
The probability that this correlation is accidental is <<0.000l and the standard error in estimating density from resistance is 0.034.
(b) Low and medium density range
From the top 7 m. of the wall of the 14 m. pit, 78 specimens were taken. The mean density was 0.429 and σ ρ = 0.043. Following a similar treatment to that in (a) above, r = 0.85 and the regression equation is
The standard error of estimating density is 0.023.
(c) Complete available density range
From the total available range of 14 m., 172 specimens were taken, including the 78 specimens considered in (b) above. The mean density was 0.475 and σρ = 0.054. Analysis shows that r = 0.92 and the regression equation is
The standard error of estimate of density is here 0.017.
The differences between the regression coefficients of Equations 2, 3 and 4 are all statistically significant, but the differences in calculated values of density given by these three formulae for a given value of the resistance are small within the density ranges where the various formulae are applicable, as is shown in Table I.
Table I Densities Given by Equations 2, 3 and 4 for Given Values of Resistance

It is estimated that errors in determining values of the resistance do not exceed 10%. These errors are due mainly to errors in measuring D. Errors in applying a correction for the frictional resistance of the length of tube below ground (or in ignoring this correction for values of l < 1 m.) should not be greater than 10%.
Thus the maximum error in determining the true resistance of a firn layer should not exceed 20%. An inspection of Table I shows that the corresponding error in density is in all cases less than 0.01 gm. cm.−3, and errors from this source do not appreciably increase the standard errors of estimate of density from resistance, using the Equations 2, 3 and 4.
(d) Effect of grain size on the resistance of low density specimens
Obviously factors other than the density have an effect on the “resistance to penetration” of a firn layer. It has not been possible to deal mathematically with such factors as the degree of compaction, but a partial correlation between resistance, density and grain size has been attempted.
Of the 40 specimens dealt with in (a) above, the mean size of 27 was measured. The mean density of these 27 specimens was 0.417 and σ ρ = 0.054. The correlation coefficient, r, between density and log resistance is 0.72 and the regression equation is
The standard error of estimate of density is 0.036. (The difference between the regression coefficients of Equations 2 and 5 is not statistically significant).
Inspection of the data shows that a further correlation exists between the logarithm of the resistance and the logarithm of the mean linear dimension of the grain. Following the normal statistical treatment for multiple correlation and treating density and grain size as independent variables the following formula is derived:
An analysis of variance associated with this formula shows that the grain size has a significant effect on the resistance, other than that due to the direct correlation between density and grain size.
The correlation coefficient between observed resistances and those calculated from Equation 6 is 0.898, and the standard error of estimate of density from this equation is reduced to 0.023.
With samples of higher density it was found that the variations in grain size are much smaller and it seems probable that the effect of these variations in grain size on the resistance is much less than in the low density specimens, but no statistical analysis of the data has been possible.
V. Conclusions
It has been shown that a direct relationship exists between the “resistance to penetration” and the density of a firn layer.
Although other factors, and particularly the grain size, affect the resistance, especially when the density is low, it is possible from the resistance of a layer of firn to determine its density. The standard error of estimate of density from resistance is less than 0.04 for all densities within the range 0.3 to 0.57, and less than 0.02 for densities between about 0.42 and 0.57.
Where the mean density is less than about 0.47 it is possible to apply corrections to the measured resistance to allow for the effect of frictional resistance between the walls of the hole and the tubes of the Rammsonde, and the density can be determined to a depth of 3 m. Where the density is greater than this, estimates of density at depths greater than 1 m. are inaccurate.
The primary reason for making this calibration of the instrument was to allow an interpretation of the Rammsonde profiles obtained at points along the gravity traverse. From these it will be possible to determine the variation of accumulation during the last ten years or so with position, along this traverse. However, it is probable that the instrument can be used in other cases where a rapid method is required for determining a density profile. It must be pointed out that the equations given above refer specifically to one particular instrument; no attempt has been made to transform “resistances” (in kilograms) into “pressures” (force per unit area). Further, as pointed out earlier, these calibration experiments have all been carried out in cold firn. Obviously the same calibration equations cannot be applied when the instrument is used under very different conditions, such as, for example, those existing in the snow of a temperate glacier. Under these conditions a recalibration would be required.
VI. Acknowledgments
With pleasure I acknowledge the help given me by other members of the Expedition. Chief Officer E. O. Jones assisted with the determinations of the densities of many of the samples and Mr. S. Paterson has given valuable advice on the statistical problems. In particular I wish to thank Mr. H. Lister for his help in the arduous task of digging the pit, in measuring grain sizes and densities, and in making the Rammsonde profiles.



