Introduction
Changes in the flow of the huge Antarctic ice sheet can significantly influence sea-level rise and are a major cause of uncertainty in the prediction of sea-level evolution (Reference SolomonSolomon and others, 2007). The basis of ice-sheet flow models is Glen’s flow law (e.g. Reference Huybrechts and NuttallHuybrechts, 2007), a power law typical for dislocation-creep controlled deformation describing ice deformation on a macroscopic scale, but the actual physical deformation or strain-rate controlling processes are not reflected in this law (Reference Alley, Clark, Huybrechts and JoughinAlley and others, 2005). Rather, it is extrapolated from creep experiments in the secondary creep stage, although the stage at which the polar ice deforms is not known.
The creep deformation of natural ice is governed by dislocation dynamics, which is highly anisotropic at the crystal scale. In the hexagonal ice Ih, the most common dislocations are those gliding on the basal plane. Two more glide-plane sets theoretically permitted by the hexagonal symmetry are nonbasal planes providing glide on the prismatic and pyramidal plane, but the peculiar behaviour of dislocations (Reference Hondoh and HondohHondoh, 2000) leads to the well-known high anisotropy of the plasticity of ice: nonbasal deformation of ice single crystals requires stresses at least 60 times larger than those activating the basal slip (Reference Duval, Ashby and AndermanDuval and others, 1983). Nonetheless, during extensive deformation by dislocation creep of polycrystalline ice, four independent slip systems are locally required (Reference HutchinsonHutchinson, 1977) in order to achieve deformation compatibility at grain boundaries (GBs). Basal glide only provides two independent slip systems, so nonbasal glide has sometimes to be activated, at least locally. This is accepted as the rate-limiting process under high-stress conditions leading to a stress exponent n Pz:i3 in Glen’s flow law, but during the low-stress deformation of polar ice sheets these processes are not yet clear (Reference Montagnat and DuvalMontagnat and Duval, 2004).
Although individual dislocations and their distribution and dynamics have frequently been observed (e.g. Reference Higashi, Fukuda, Shoji, Oguro, Hondoh and Goto-AzumaHigashi and others, 1988; Reference BakerBaker, 2003), slip system activity can only be observed if dislocations (of the same type) occur frequently enough to exert deformation. Well-developed dislocation walls (subGBs) are easy to observe with optical methods such as polarization methods (Reference Durand, Perrson, Samyn and SvenssonDurand and others, 2008) or microstructure mapping (Reference KipfstuhlKipfstuhl and others, 2006). SubGB grooves have been proven to be typical deformation-induced structures (Reference Hamann, Weikusat, Azuma and KipfstuhlHamann and others, 2007) and to occur frequently in a polar ice core (EDML; Reference Weikusat, Kipfstuhl, Faria, Azuma and MiyamotoWeikusat and others, 2009b). Remarkably, subGBs observed in such high spatial resolution as provided by microstructure mapping reveal distinct characteristics in shape and arrangement with respect to the c-axes orientations of the individual crystals (Reference Hamann, Weikusat, Azuma and KipfstuhlHamann and others, 2007; Reference Weikusat, Kipfstuhl, Azuma, Faria, Miyamoto and HondohWeikusat and others, 2009): straight subGBs occur parallel to the basal plane trace (intersection line of basal plane with the sectioned observation plane), whereas zigzag-shaped substructures are observed, typically in their main direction, showing high angles to the basal plane and parallel to the basal plane in their shorter segments (Fig. 1).
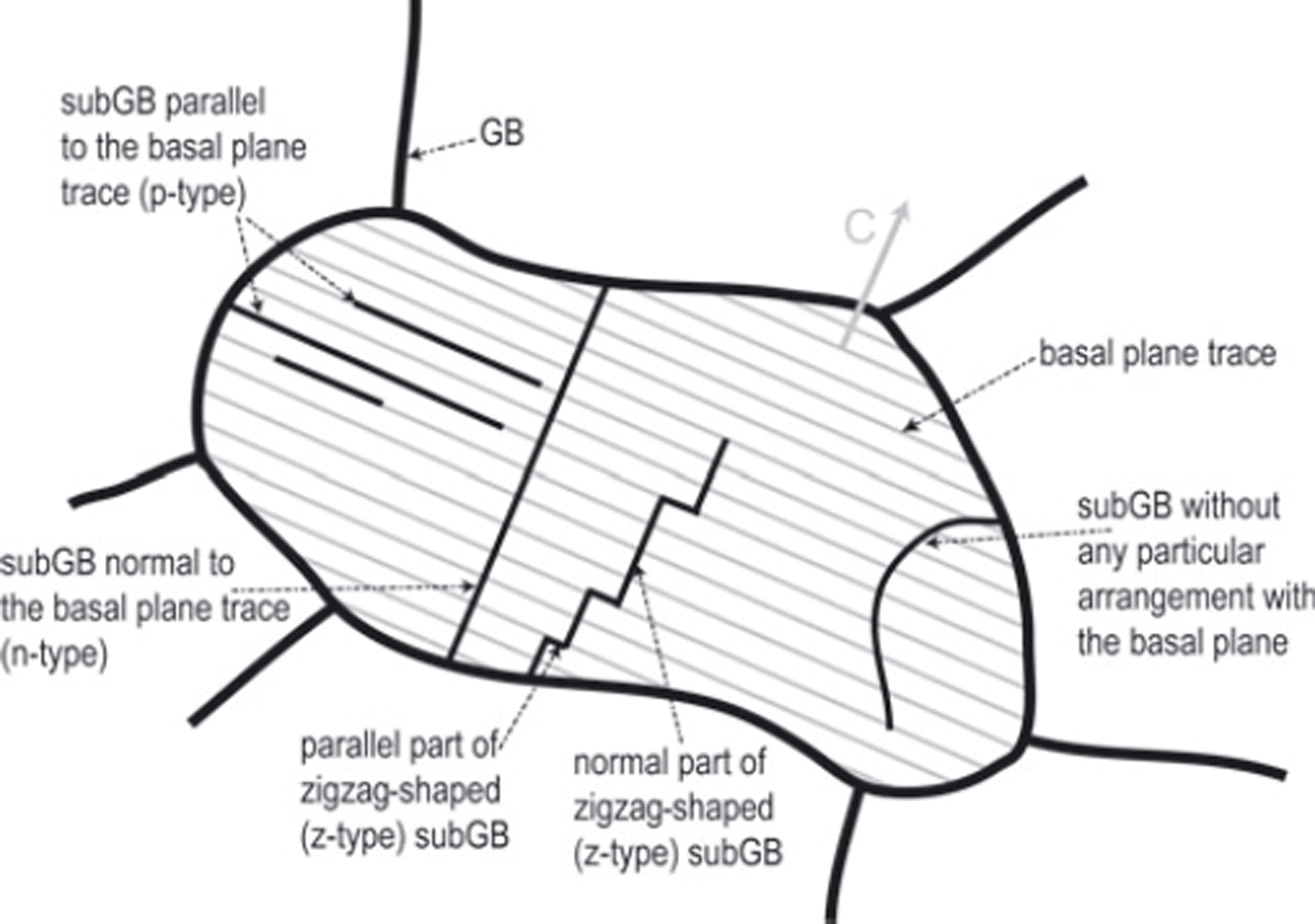
Fig. 1. Schematic description of subGB types described by Reference Hamann, Weikusat, Azuma and KipfstuhlHamann and others (2007) and Reference Weikusat, Kipfstuhl, Azuma, Faria, Miyamoto and HondohWeikusat and others (2009a,Reference Weikusat, Kipfstuhl, Faria, Azuma and Miyamotob). Modified after figure 7a in Reference Weikusat, Kipfstuhl, Faria, Azuma and MiyamotoWeikusat and others (2009b). Note: as the crystal orientation data are taken as line scans (1-D track), the z-type subGB is classified either as normal or as parallel, depending on the very local subGB segment, where the X-ray Laue line scan crosses the subGB.
Full three-dimensional (3-D) crystal-orientation changes across such typical subGBs were determined using X-ray Laue diffraction (Reference Miyamoto, Weikusat and HondohMiyamoto and others, 2011) in order to:
-
validate and specify the microstructure mapping images and
-
further characterize the different types of grain substructures with respect to the high mechanic anisotropy of the hexagonal ice crystal.
Here we present misorientation data and observations on subgrain boundaries in natural polar ice.
Methods and Material
Samples were obtained from the EPICA (European Project for Ice Coring in Antarctica) deep ice core from Dronning Maud Land (EDML) and from one shallow core (B37), drilled between 2003 and 2006 at Kohnen station (75°00′ S, 0°40′ E; 2892 m a.s.l.), East Antarctica. The EDML drill site is located on a flank ∼5 km from an ice divide with a horizontal flow velocity at the surface of 0.76 m a−1 (Reference Wesche, Eisen, Oerter, Schulte and SteinhageWesche and others, 2007). Samples were stored at −30°C after transportation at −25°C from Antarctica to Bremerhaven, Germany. Thin sections from vertically cut samples (∼50 × 2 mm) were prepared in a −25°C cold laboratory in Bremerhaven using a microtome according to standard procedures, but using X-ray transparent plastic plates instead of glass plates. Microstructure mapping (Reference KipfstuhlKipfstuhl and others, 2006) was performed in order to obtain an overview of the present features under an optical microscope. This method uses sublimation as an etching technique to visualize GBs as grooves at a very high spatial resolution (one-pixel edge ∼3.3 μm). A distinction between high-angle GBs and small-angle subGBs is associated with a discontinuity in the boundaries’ properties (e.g. Reference Gottstein and ShvindlermanGottstein and others, 1999), so here the different sublimation behaviour (Reference Saylor and RohrerSaylor and Rohrer, 1999) can be used to distinguish between deep grooves, i.e. dark GBs, and shallower grooves, i.e. grey subGBs (Reference KipfstuhlKipfstuhl and others, 2006; Reference Hamann, Weikusat, Azuma and KipfstuhlHamann and others, 2007; Reference Weikusat, Kipfstuhl, Faria, Azuma and MiyamotoWeikusat and others, 2009b). Typical examples of such structures were selected, and crystal orientations were measured by means of X-ray Laue diffraction (Reference Miyamoto, Shoji, Hori, Hondoh, Clausen and WatanabeMiyamoto and others, 2005, Reference Miyamoto, Weikusat and Hondoh2011).
In total, 83 grains in samples from 15 different depths (115–2702 m) from Holocene ice to marine isotope stage 6 (MIS6) or even MIS7? ice (Reference RuthRuth and others, 2007) were measured and ∼240 individual subGBs were characterized.
Results
Validation of microstructure mapping
Microstructure mapping reveals grooves along lattice mis-orientation boundaries, which were qualitatively validated using crossed polarizers additionally to the sublimation technique (e.g. fig. 4 in Reference Wang, Kipfstuhl, Azuma, Thorsteinsson and MillerWang and others, 2003; fig. 6 in Reference KipfstuhlKipfstuhl and others, 2006). However, a high-resolution crystallographic technique can quantitatively verify the misorientations. Misorientation angles, θ, across GBs have been measured (Fig. 2) and, as expected, show c-axes misorientations ranging from a few degrees to almost 90°.
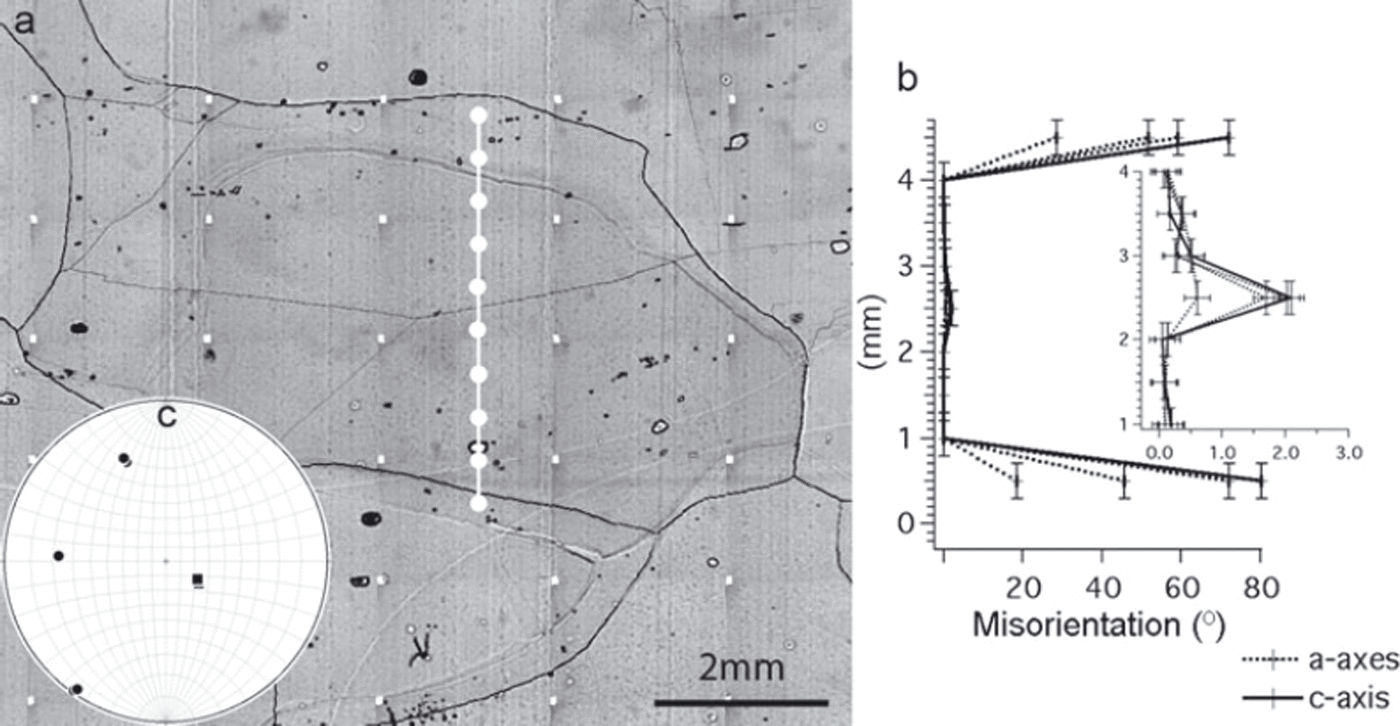
Fig. 2. Misorientation data across GBs (2365.8 m depth). (a) Microstructure mapping image with track of orientation measurements (white circles). Dark thick black lines: GBs. Thin lines: subGBs. GB grooves from the lower surface of the thin section are visible as unfocused lines, indicating inclination of GBs in three dimensions. (b) Misorientations between neighbouring points calculated from X-ray Laue measurements. (b) is placed according to (a), i.e. y = 0 mm is equal with lowest white circle in (a). Insert shows detail of (b) with different scale of misorientations axis. (c) Stereographic projection of c-axes (box symbols) and a-axes (circle symbols) to illustrate the general orientation of the centre grain. The basal plane is the great circle formed by the three a-axes.
Whether all structures are revealed by microstructure mapping can be demonstrated by observing the orientations within ‘clean’ grains without any sublimation substructures visible with the optical microscope (Fig. 3). Such undisturbed grains or grain parts reveal only some noise below 0.5°, which can thus be regarded as the angular resolution of the misorientation measurements.
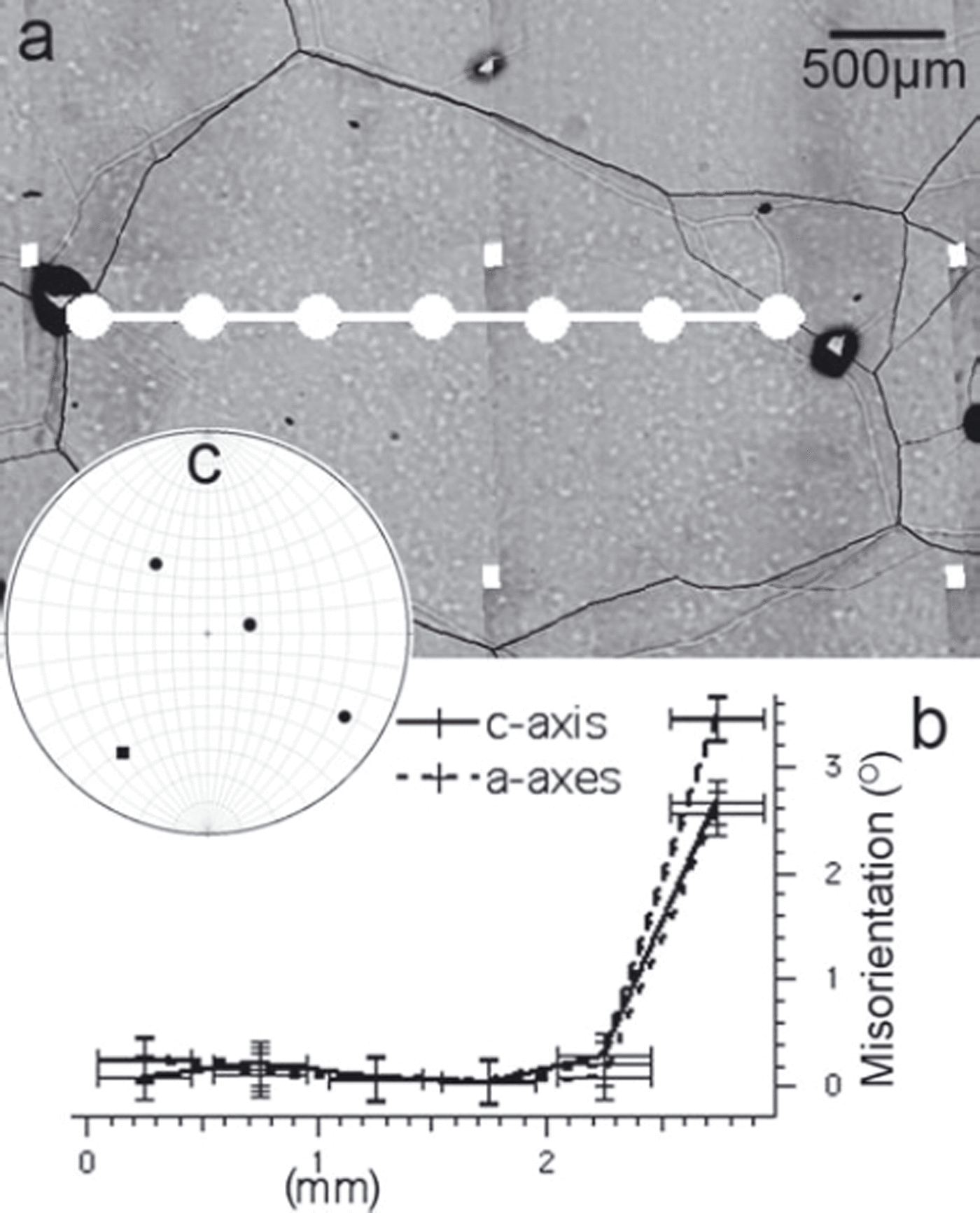
Fig. 3. Misorientation data within a sublimation feature-free grain (454.8 m depth). (a–c) as in Figure 2. Misorientations among neighbouring points within the centre grain are less than 0.5°, the angular resolution.
Subgrain boundaries
SubGBs appear as shallow grooves (thin grey lines) in the microstructure mapping image due to the sublimation behaviour depending on its misorientation angle (Reference Saylor and RohrerSaylor and Rohrer, 1999). Indeed, X-ray Laue orientation measurements reveal higher misorientations at deep sublimation grooves (GBs) compared to shallow sublimation grooves (subGBs) (Fig. 2b and insert). Frequencies of misorientations measured across such thin sublimation features are given in Table 1. It is remarkable that a high fraction (42%) of subGBs cannot be detected by their c-axis misorientations (θc <0.5°) and that only a few subGBs have misorientations >3°.
Table 1. Frequencies of misorientations across shallow sublimation grooves (total number of subGBs measured: n ≈ 240)

A correlation of subGB misorientation angles with grain microstructure data (grain size, grain aspect ratio, grain irregularity, grain elongation direction) cannot be observed. The orientation of c-axes (angle between the vertical core axis as overall main compression direction and the c-axes) cannot be correlated with misorientation angles.
Another important observation regarding subGBs is their preferred occurrence close to GBs, and especially close to peculiar shapes of GBs: for example, subGBs typically show up at the outside of smoothly curved GBs (Reference Weikusat, Kipfstuhl, Faria, Azuma and MiyamotoWeikusat and others, 2009b), but they are frequently also directly attached to edges or necking GBs.
Subgrain boundary types
For ∼70% of all subGBs, misorientation in c- or a-axes was high enough to be detected. Examining the misorientations of c- and a-axes separately (e.g. θc and θa in Figs 2b and 3b) enables an immediate recognition of the misorientation rotation axis. Observed configurations of misorientations, shown schematically in Figure 4, are:
Arbitrary misorientation rotation axis: The rotation axis is not (close to) a crystallographic axis, so none of the four calculated misorientations of the crystallographic axes is particularly low (Fig. 4a; for an example see Fig. 5). This is the case for ∼23% of all subGBs with a detectable misorientation
c-axis is (close to) misorientation rotation axis: The misorientation of the c-axis is significantly lower (i.e. 0 within measurement accuracy) than those of the a-axes (Fig. 4b; for an example see Fig. 6) in ∼8% of the subGBs.
One a-axis is (close to) misorientation rotation axis: The majority (∼70%) of all subGBs with misorientation >0.5° show misorientation of one a-axis significantly lower (i.e. 0 within measurement accuracy) than those of the other three crystal axes (Fig. 4c; for an example see Figs 7 and 8).
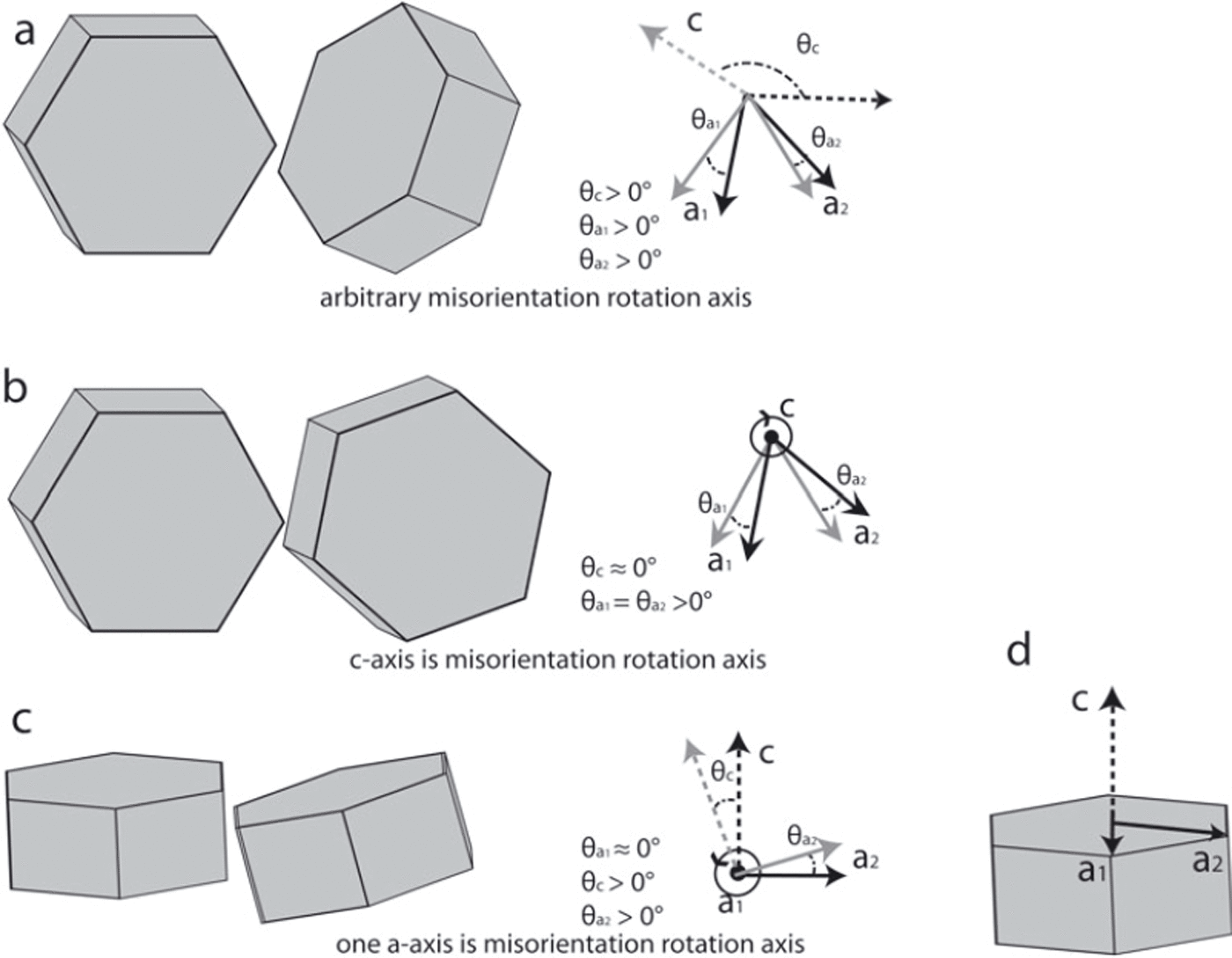
Fig. 4. Rotation axes generating different configurations of misorientation. (a) Schematic of two crystals rotated around an arbitrary axis with respect to each other (left) and the two corresponding systems of crystal axes showing all misorientation angles (right). (b) Schematic of two crystals oriented to each other by rotation around the c-axis (left) and the two corresponding systems of crystal axes, with c being normal to the image plane, showing all misorientation angles (right). (c) Schematic of two crystals misoriented by rotation around one a-axis (left) and the two corresponding systems of crystal axes, with a 1 being normal to the image plane, showing all misorientation angles (right). (d) Crystal axes with schematic crystal.
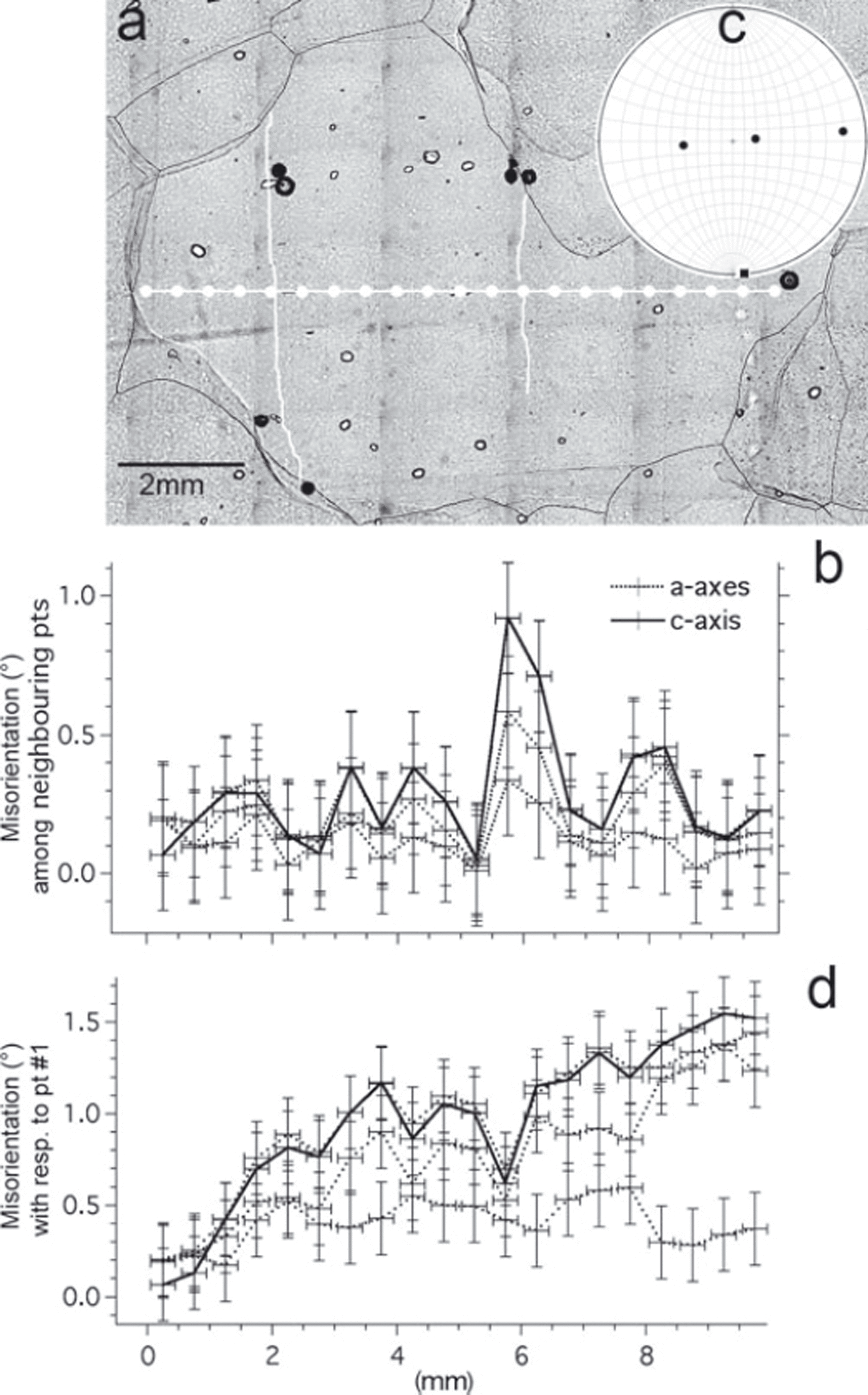
Fig. 5. Misorientation data across two subGBs highlighted in white (1855.9 m depth). (a–c) as in Figure 2. Left subGB has misorientation below the detection limit. Right subGB has no particularly low misorientation in the c- or one a-axis. (d) Misorientation with respect to the leftmost measurement point in a at x = 0 mm shows a gradient in misorientation and a significantly low value in one axis despite the arbitrary rotation axis close to the subGB.
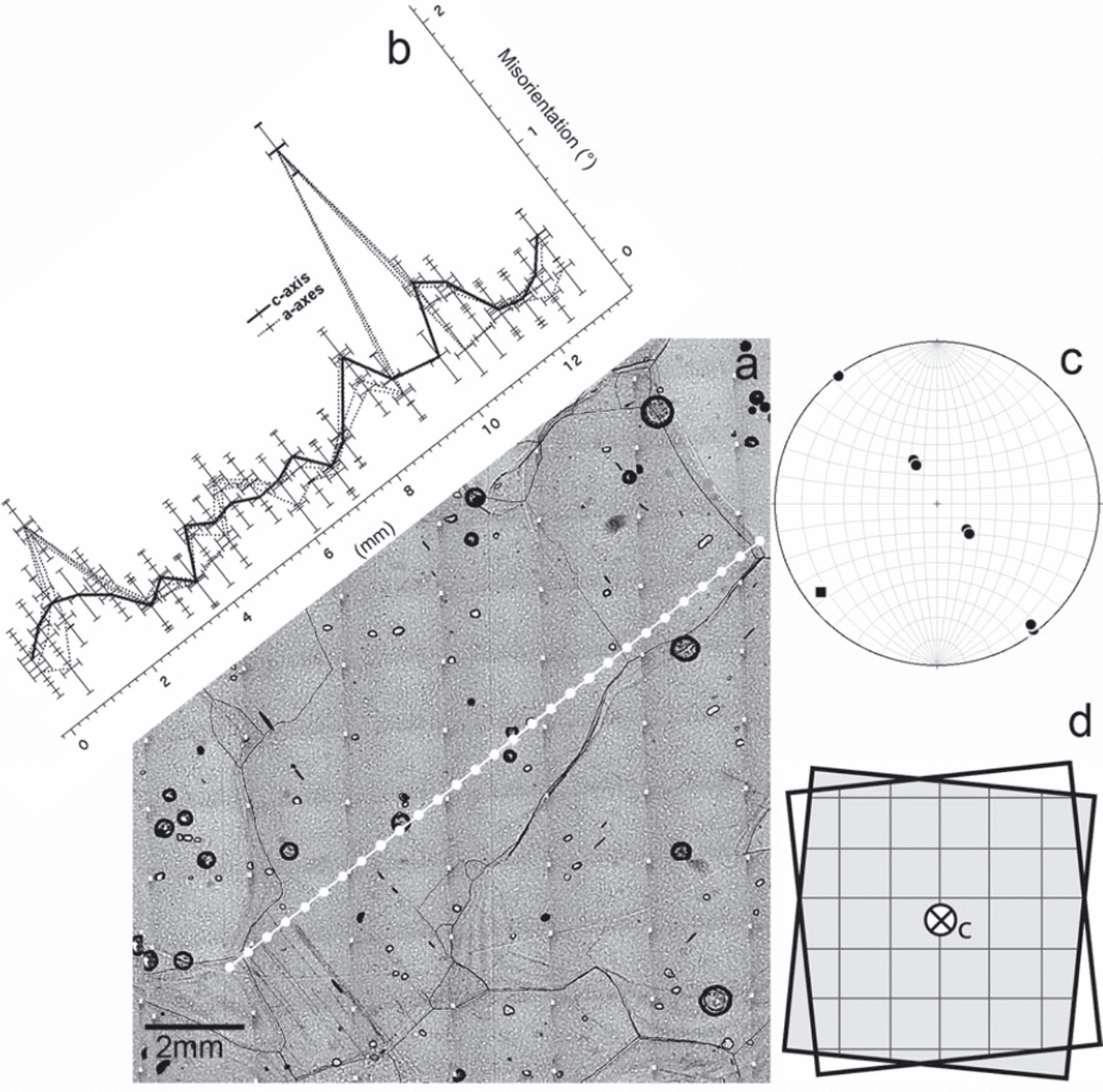
Fig. 6. Misorientation data across several subGBs parallel to the basal plane trace (1855.9 m depth). (a–c) as in Figure 2. Multiple subGBs at x < 2 mm cannot be resolved due to the spatial resolution. The misorientation across subGB at x = 10 mm shows that the c-axis has a significantly lower value than the three a-axes. (d) Schematic illustration of the configuration of a rotation around the c-axis assuming a dislocation wall composed of screw dislocations lying in the basal plane. This configuration describes a twist boundary comprising two sets of screw dislocations in the basal plane with Burgers vectors b = a.
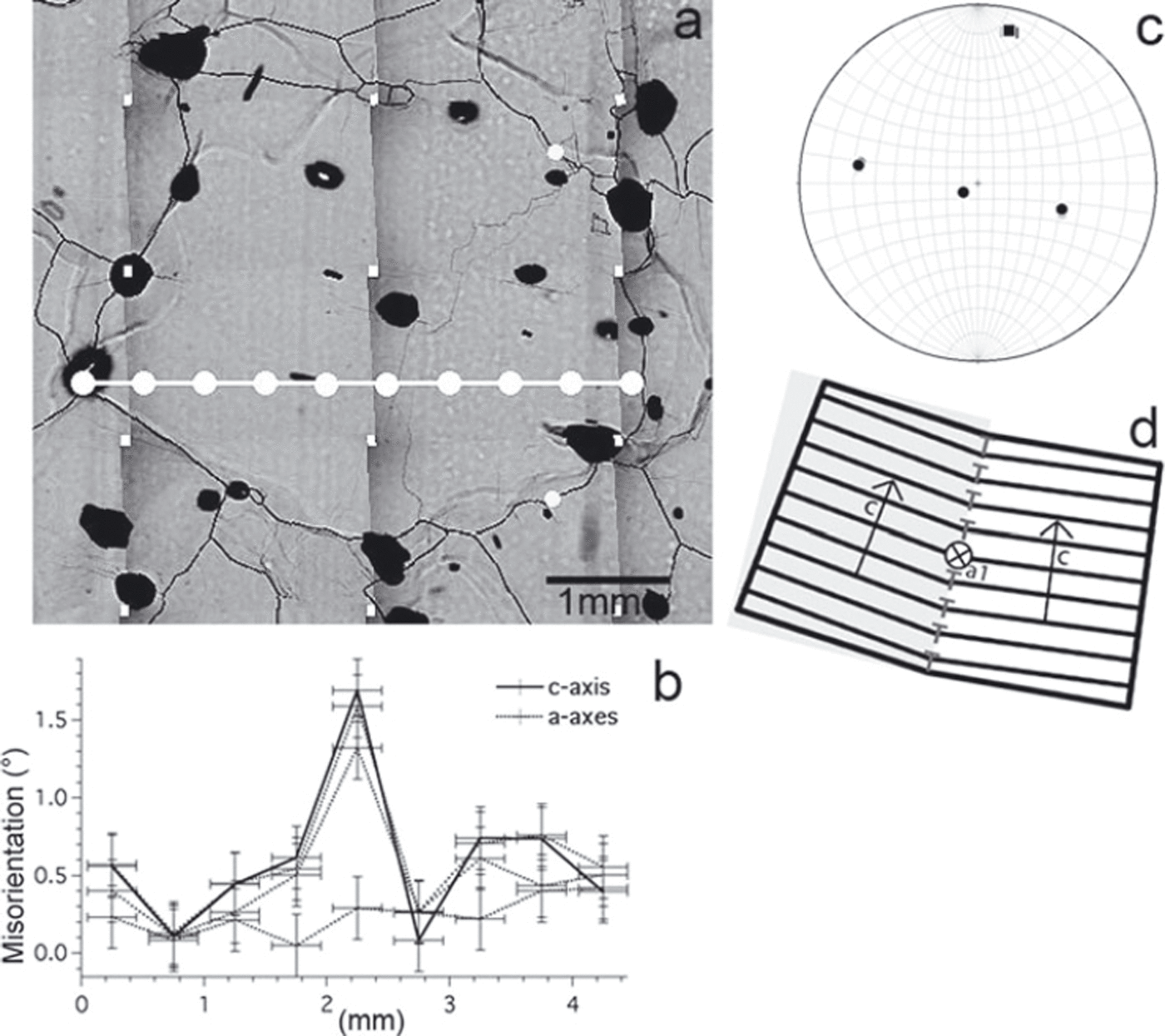
Fig. 7. Misorientation data of a subGB normal to the basal plane trace (655.9 m depth). (a–c) as in Figure 2. One a-axis has a significantly lower misorientation value than the other three axes across the subGB (x = 2.25 mm). (d) Schematic illustration of the configuration of a dislocation wall composed of edge dislocations perpendicular to the basal plane indicated by ‘T’ and the rotation axis, a 1. This configuration describes a tilt boundary comprising edge dislocations in the basal plane with Burgers vector b = a.
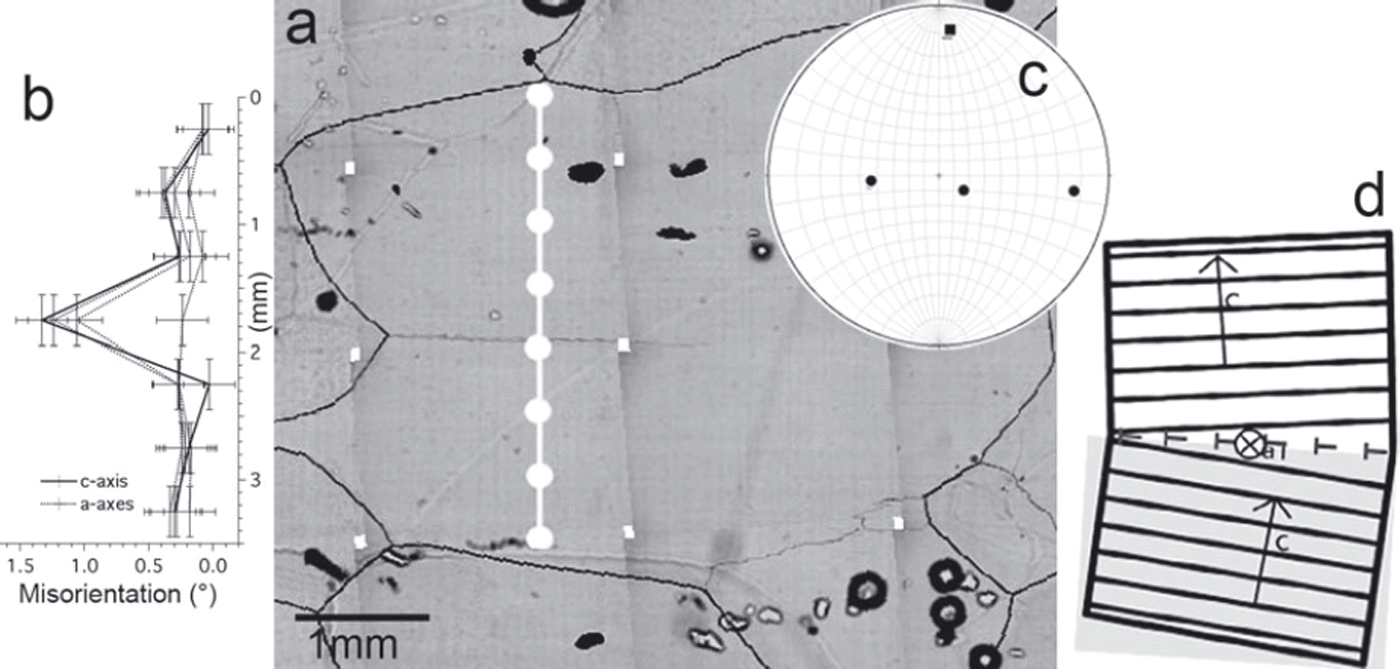
Fig. 8. Misorientation data of a subGB parallel to the basal plane trace (1204.1 m depth). (a–c) as in Figure 2. One a-axis has a significantly lower value than the other three axes across the subGB (x = 1.75 mm). (d) Schematic illustration of the configuration of a dislocation wall composed of edge dislocations parallel to the basal plane indicated by ‘T’ and the rotation axis, a 1. This configuration describes a tilt boundary comprising dislocations in a nonbasal plane with Burgers vector b = c or b = c0+ a.
Characteristic subGB types discovered with microstructure mapping (Reference Hamann, Weikusat, Azuma and KipfstuhlHamann and others, 2007; Reference Weikusat, Kipfstuhl, Azuma, Faria, Miyamoto and HondohWeikusat and others, 2009a,Reference Weikusat, Kipfstuhl, Faria, Azuma and Miyamotob) can be summarized by their basic arrangement (Fig. 1):
normal to the basal plane: either of long and straight shape (n-type; Fig. 1) like the classical conception of a grain undergoing polygonization (Reference NakayaNakaya, 1958; Reference Alley, Gow and MeeseAlley and others, 1995, fig. 2) or rather short as segment of irregularly zigzag or step-like shaped subGB (z-type; Fig. 1).
parallel to the basal plane: straight shallow sublimation grooves (p-type; Fig. 1), typically occurring in peculiar swarms of multiple subGBs parallel to each other. (Although some segments of irregularly zigzag-shaped subGB can also be parallel to the basal plane (z-type; Fig. 1), the normal segments are typically the dominant features.)
no particular arrangement with the basal plane: typically bowed smooth shapes resembling GBs (Fig. 1), but as shallow sublimation grooves.
The observation of these characteristic arrangements with respect to the crystallography of the crystal is in accordance with observations from X-ray diffraction topography on laboratory-grown ice single crystals shown as an example in Figure 9: higher dislocation densities accumulated in planes normal to the basal plane (Fig. 9a), and higher-dislocationdensity regions developed parallel to the basal plane (Fig. 9a–c). Figure 9e reveals complex interaction of such planes in basal and in prismatic orientation leading to a zigzag arrangement (Fig. 9d). The similarity in arrangement of subGB and higher-dislocation-density regions with respect to the crystallography of ice suggests that the formation processes are related or rely on similar mechanisms. The regions of possible subGB formation may be preestablished by the observed variations in dislocation density. Among the regions of high dislocation density, only some develop further by accumulating more dislocations and only those with highest energy are revealed by sublimation, leading to the peculiar step-shaped subGB groove. Details on X-ray diffraction topography method and further images of local variations in dislocation density are provided by Reference Higashi, Fukuda, Shoji, Oguro, Hondoh and Goto-AzumaHigashi and others (1988).

Fig. 9. X-ray diffraction topographs (for method description see Reference Higashi, Fukuda, Shoji, Oguro, Hondoh and Goto-AzumaHigashi and others, 1988) from laboratory-grown ice single crystals. Grey-value contrasts indicate variations in dislocation density and in configuration of dislocations and in direction of the diffraction vector, g. Orientation of c-axes is identical in all five images (vertical). The direction of the diffraction vector g is given. (a) Stable walls of higher dislocation density normal to the basal plane (upper rim of plane indicated by dotted line and white arrows) and stable walls of higher dislocation density parallel to basal plane (black arrow indicates a strong example of many more horizontal dislocation walls). (b) Stable dislocation wall parallel to basal plane exhibited as a horizontal dark band indicated by arrows (diffraction vector is ![]() ). (c) X-ray topograph of the same crystal as (b), but with diffraction vector [0002]. The same dislocation wall indicated by the arrows in (b) displays a strong band here, which shows that this wall consists mainly of dislocations with the Burgers vector b = c. (d) Zigzag structure of regions of higher dislocation density. (e) Interacting walls parallel to basal (black arrows) and prismatic planes (white arrows).
). (c) X-ray topograph of the same crystal as (b), but with diffraction vector [0002]. The same dislocation wall indicated by the arrows in (b) displays a strong band here, which shows that this wall consists mainly of dislocations with the Burgers vector b = c. (d) Zigzag structure of regions of higher dislocation density. (e) Interacting walls parallel to basal (black arrows) and prismatic planes (white arrows).
Combining the information on misorientation rotation axes and arrangement with respect to the basal plane gives additional information to characterize subGBs (Table 2). Boundaries arranged normal to the trace of the basal plane are not further distinguished here into n-type and z-type, because X-ray Laue measurements are collected as one-dimensional (1-D) line scans, so misorientation measurements cross the z-type boundaries at the typically longer part which is normal to the basal plane trace. All basal-plane normal subGBs, where a misorientation axis close to the crystal axes could be determined, originate from rotations around one a-axis (Table 2; example in Fig. 7), whereas basalplane-trace parallel subGBs with a rotation axis close to the crystallographic directions can be divided into two types: (1) originating from a rotation around one a-axis (example in Fig. 8) and (2) originating from a rotation around the c-axis (example in Fig. 6). Approximately one-third of all subGBs cannot be classified easily either by their arrangement or by their rotation axis. Remarkably, no boundary normal to the basal plane and rotated around an a-axis was observed.
Table 2. Absolute number frequencies of all subGBs with detectable misorientations (>0.5°; n = 165)

Discussion
Observations of the expected high misorientations across GBs, low misorientations across subGBs and the very low fluctuations within undeformed grains free of sublimation features verify that all subGBs are revealed by sublimation used for microstructure mapping. The observation that shallowest sublimation grooves can be observed reliably with microstructure mapping, but have very small misorientations (<0.5°), proves microstructure mapping is an extremely sensitive method to visualize very small lattice misorientations.
Implications on energies of subgrain boundaries
An easy correlation of groove depth, i.e. grey value in the microstructure mapping images, could not be found, however, probably because of other factors influencing the sublimation, such as the angle between boundary plane and section surface: the optimal thermal grooving (Reference MullinsMullins, 1957) can be obtained if the boundary is perpendicular to the surface, whereas an oblique intersection of boundary and surface produces oblique grooves which do not achieve the maximum possible depth. Furthermore, GB thickness generally varies with impurities (e.g. Reference BarnesBarnes, 2003) which are not considered in this study. Nevertheless, the definite difference in groove depth between GBs and subGBs indicates an abrupt transition in the sublimation behaviour due to GB energy.
Measurements of GB energies for ice are available for larger misorientation boundaries (Reference SuzukiSuzuki, 1970). However, our observations allow some discussion of GB energies for small-angle boundaries, because the thermal-etching groove depth, i.e. surface dihedral angle of the groove, ψ S, depends on the ratio of GB energy, γ, and surface energy, γ S (Reference Saylor and RohrerSaylor and Rohrer, 1999),
assuming that the surface energy is isotropic. The GB energy, γ, of a small-angle grain boundary is in turn correlated to the misorientation angle, θ (Reference Read and ShockleyRead and Shockley, 1950; Reference Hirth and LotheHirth and Lothe, 1982):
with γ 0 and A depending on the character and orientation of the boundary and the form of the dislocation arrangement (shear modulus, Burgers vector and Poisson ratio; core parameters of dislocation sets). We observed that very low θ (<0.5°) produces thermal grooves, requiring that γ has a very steep slope in the γ−θ space in this range, i.e. GB energy is low only for tiny misorientations (∼<0.1°) and reaches a certain critical-threshold GB energy, γ C, to produce grooves at low misorientations. It can thus be predicted that a very fast increase in GB energy should occur in the lower misorientation range, which is consistent with the estimated development for smallest values of γ by Reference SuzukiSuzuki (1970).
Using the dislocation spacing, D, derived by Frank’s formula (Humphreys, 2004),
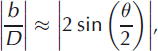
with b being the Burgers vector of the dislocation (4.52 Å for basal dislocations and 7.36 or 8.63 Å for nonbasal dislocations), and the energy of single dislocations
with G being the shear modulus (4 × 29 N m−2), an upper bound of the energy of a subGB can be estimated:
For the measured typical misorientations (0.5–3°) for boundaries with dislocations in the basal plane, the estimated values for γ range from 8 to 47 mJ m−2. This is about 8–50% of the energy usually assumed for high-angle grain boundaries in ice (65 mJ m−2 (Reference HobbsHobbs, 1974, p. 440) and 60–100 mJ m−2 (Reference SuzukiSuzuki, 1970)). Highest misorientations of ∼5° were observed across shallow sublimation grooves showing the classical tilt geometry with edge dislocations in the basal plane. These boundaries have energies, γ, of 79 mJ m−2 which is well within the range of high-angle grain boundaries. Misorientations for boundaries with dislocations on nonbasal planes range from 0.5° to 4°, but their energy has to be estimated significantly higher (3–90 mJ m−2) due to the larger Burgers vector of c or c + a dislocations. This finding is supported by subGB energy estimates using Equation (2): as well as larger Burgers vectors, the angle of the boundary with the basal plane is included in this estimation (Reference Read and ShockleyRead and Shockley, 1950), causing higher γ values for boundaries with dislocations on nonbasal planes (10–20%) than for other subGB types. The GB–subGB geometry in Figure 8 indeed seems to indicate a higher energy than expected for a subGB: the dihedral angles appear almost equilibrated for boundaries of similar energy. This finding is common with the strongest parallel subGB grooves with rotation around one a-axis. From the boundary energy estimates and the observations on groove depth, we can expect that the subGB–GB threshold angle is 4–5° for boundaries with basal dislocations, but close to 3° for boundaries with nonbasal dislocations. Note that the estimations using Equations (2) and (5) give upper bounds of GB energies considering stable states of dislocation walls. However, most cases observed during this study probably represent unstable states with even higher energies than those estimated here.
The sudden transition in the sublimation behaviour of GBs and subGBs is due to different boundary structures of GB and subGB: subGBs are strictly periodic crystal dislocation arrangements which minimize the GB energy. In GBs dislocation cores tend to overlap and to lose their identity as individual lattice defects (Reference Gottstein and ShvindlermanGottstein and Shvindlerman, 1999). The observation of strong, regular and deep etch grooves from misorientation θ ≈ 4–90° indicates a similar structure for all grain boundaries, whereas the appearance variability of subGBs may be due to a multitude of boundary types (e.g. tilt boundaries and twist boundaries) which are expected to have different energies, apart from misorientation differences. For instance, Equation (2) is strictly valid only for one-dislocation set tilt boundaries with small misorientation angles.
Implications on dislocation types
Although the actual characteristic structures of dislocations in ice are very peculiar and rather complicated (Reference Hondoh and HondohHondoh, 2000), the combined information on misorientation rotation axes and arrangement with respect to the basal plane allow basic inferences regarding the activity of different dislocation types.
Basal tilt boundary: A dislocation wall accumulating dislocations normal to the basal plane and a resulting rotation around one a-axis can be produced by an array of basal edge dislocations with Burgers vector b = a (Fig. 7d). The vast majority of all measured subGBs perpendicular to the basal plane are indeed mainly composed of basal edge dislocations, and thus are basal tilt boundaries (Table 2).
Basal twist boundary: A dislocation wall parallel to the basal plane and a resulting rotation around the c-axis can be produced by two sets of basal screw dislocations with Burgers vectors b = a (Fig. 6d). Only ∼16% of all measured parallel subGBs are basal twist boundaries (Table 2).
Nonbasal tilt boundary: A dislocation wall accumulating dislocations parallel to the basal plane and a resulting rotation around one a-axis can be produced by an array of nonbasal edge dislocations with Burgers vector b = c or b = c + a (Fig. 8d). X-ray diffraction topographs using different diffraction vectors (![]() and [0002]) confirm the occurrence of walls mainly consisting of dislocations with the Burgers vector b = c (Fig. 9b and c). More than half of all measured parallel subGBs are nonbasal tilt boundaries (Table 2).
and [0002]) confirm the occurrence of walls mainly consisting of dislocations with the Burgers vector b = c (Fig. 9b and c). More than half of all measured parallel subGBs are nonbasal tilt boundaries (Table 2).
The observations of this study and the interpretation given above led to the theoretical considerations by Reference Hondoh and HondohHondoh (2009).
One-third of all subGBs measured here cannot be specified regarding a dominant activity of dislocation types, and thus are probably mixed boundaries composed of mixed dislocations, which is usually considered to be the typical appearance of dislocations (e.g. Reference Hull and BaconHull and Bacon, 1984; Reference Weertman and WeertmanWeertman and Weertman, 1992). However, as only a limited amount of subGBs could be measured with the semi-automatic X-ray Laue diffraction method and the obvious typical types (normal and parallel) may have been favoured unintentionally, the subGBs with no particular shape and arrangement, i.e. mixed boundaries, might be under-represented in this study. However, the finding that among the typical subGB types the almost pure nonbasal tilt boundary is the second frequent boundary type together with the basal tilt boundary indicates that nonbasal edge dislocations cannot be neglected concerning the deformation around EDML.
Conclusions
X-ray Laue diffraction validates and quantifies the occurrence of sublimation grooves along GBs and subGBs observed with microstructure mapping. Misorientation values of subGB in natural ice range from <0.5° to 4°.
A combination of full crystallographic analyses and geometrical information enables subgrain boundary types to be identified. Basal tilt boundaries composed of basal edge dislocations (b = a) have been found as basal-plane normal features caused by a rotation around one a-axis, which describes a symmetric bending of the basal plane. Basal twist boundaries composed of sets of basal screw dislocations (b = a) could be identified as basal-plane parallel features caused by a rotation around the c-axis, which describes a rotation of basal planes above each other. Geometries of subGB as basal-plane parallel features caused by a rotation around one a-axis, which describes a bending of pyramidal or prism planes, can be interpreted as nonbasal tilt boundaries comprising edge dislocations on nonbasal planes (b = c or c + a).
Boundary energies estimated using the measured mis-orientation angles and characteristics of the dislocation types give values of 8–90 mJ m−2. Note that the highest boundary-energy values, which are within the range of high-angle grain boundaries, are obtained with nonbasal tilt boundaries. Due to this finding, the threshold angle for GB–subGB transition can be expected to be less for nonbasal boundaries (∼3°) than for basal boundaries (4–5°).
The combination of X-ray Laue diffraction and microstructure mapping shows that nonbasal tilt boundaries and thus nonbasal edge dislocations are frequent subGBs and should not be neglected for the deformation under low-stress deformation of the Antarctic ice sheet in Dronning Maud Land.
Acknowledgements
This project was funded by the German Science Foundation (DFG HA 5675/1-1 and WE 4695/1-2) and supported by travel grants in the framework of a cooperation agreement between the German Science Foundation (DFG) and the Japanese Society for the Promotion of Science. This work is a contribution to the European Project for Ice Coring in Antarctica (EPICA), a joint European Science Foundation/ European Commission scientific programme, funded by the EU and by national contributions from Belgium, Denmark, France, Germany, Italy, the Netherlands, Norway, Sweden, Switzerland and the United Kingdom. The main logistic support was provided by Institut Polaire Français–Emile Victor (IPEV) and Programma Nazionale di Ricerche in Antartide (PNRA) (at Dome C) and the Alfred Wegner Institute (at Dronning Maud Land). This is EPICA publication No. 273. We thank P. Duval and D. Samyn for helpful comments and discussion.













