1. Introduction
Data in the form of time series obtained from ice cores have proved to be valuable high-resolution climate records (e.g. Reference DelmasDelmas, 1992; EPICA community members, 2004). The goal of most data processing is to retrieve relevant information from a dataset in an objective and reproducible way. Useful signals might be obtained in both the time and frequency domains. Depending on the time-scale of interest, longer trends and events on short time-scales may have different significance in a study. The identification of peaks (episodic events) in ice-core time series is of fundamental interest with respect to finding dating horizons such as volcanic tracers. These horizons are important tie points both for dating by annual-layer counting and for depth–age modelling. Once the volcanic peaks are identified and dated, a volcanic chronology may be established. In addition, based on the chronology, a mass-balance record may be established for an area (Reference Karlo¨fKarlöf and others, 2000; Reference HofstedeHofstede and others, 2004). To identify the processes behind the recording of a signal in the snow, it may require objective processing to be reproducible. For example, sulphuric acid is the most important component of volcanic deposits in the snow. Explosive eruptions emit sulphur, which is transformed to sulphuric acid in the atmosphere. However, background aerosol mainly derived from marine biogenic activity also contributes to the recorded signal. As the marine signal has high year-to-year variability (Reference Legrand and DelmasLegrand, 1995), it might obscure the correct peaks and make them difficult to unambiguously identify.
Ice-core and other geophysical records can be divided into a dynamical part (Dt ) and a noise part (Nt ) expressed as Xt = Dt + Nt . The fundamental challenge is then to separate the significant dynamical part from the noise. In this study, the dynamical part is a peak. Moreover, the dynamical part has a background level, and it is the significant deviations from this background level over a finite length in time (or ice-core depth) that are defined as peaks.
In the last two decades, many studies have been performed to either determine volcanic peaks to establish a mass-balance record, when the peaks are known and dated independently (e.g. Reference Oerter, Graf, Wilhelms, Minikin and MillerOerter and others, 1999, Reference Oerter2000; Reference Karlo¨fKarlöf and others, 2000; Reference HofstedeHofstede and others, 2004) or establish a volcanic chronology when the core has been dated by other means (e.g. Reference Legrand and DelmasLegrand and Delmas, 1987; Reference Moore, Narita and MaenoMoore and others, 1991; Reference DelmasDelmas and others, 1992; Reference Cole-Dai, Mosley-Thompson and ThompsonCole-Dai and others, 1997; Reference Traufetter, Oerter, Fischer, Weller and MillerTraufetter and others, 2004). The techniques presented here, as well as earlier work (e.g. Reference DelmasDelmas and others, 1992; Reference MayewskiMayewski and others, 1993; Reference ZielinskiZielinski and others, 1994; Reference Fischer, Wagenbach and KipfstuhlFischer and others, 1998; Reference Karlo¨fKarlöf and others, 2000), first attempt to define a background, which in turn is subtracted from the original time series. The residuals, i.e. the high-frequency part of the original time series, are subjected to a different statistical treatment in order to define a threshold for a peak. Both multivariate discriminant analysis and simpler variance-based thresholds have been proposed (e.g. Reference DelmasDelmas and others, 1992; Reference ZielinskiZielinski and others, 1994; Reference Cole-Dai, Mosley-Thompson and ThompsonCole-Dai and others, 1997). The different studies have made use of different filtering techniques to define the background level: spline-based methods (Reference ZielinskiZielinski and others, 1994), median filter (Reference Fischer, Wagenbach and KipfstuhlFischer and others, 1998) or Savitsky–Golay filter (Reference Karlo¨fKarlöf and others, 2000). Regardless of which filtering technique has been used, the primary objective of the filtering is to define the background level by filtering out climate and measurement- induced trends as well as blocking periods shorter than the episodic event of interest. Filtering is not a fully objective procedure, as the correct choice of filter lengths, i.e. cut-off frequencies, requires good knowledge of the data and is dependent on the skill of the operator. However, it is a very important part of successful data processing.
In this paper, we examine and evaluate five different statistical techniques for the selection of thresholds for peak signals in ice-core data. The motivation for doing so is to investigate whether objective and robust techniques in the future could be established as standards for finding peaks in palaeoclimatic records. The techniques presented in this paper identify events of significant amplitude in ice-core records. The time series contain peaks of volcanic origin, but the presented techniques may have merit for other data when studying short-scale anomalies in other environmental records. In this paper, there is no attempt to describe the origin of the events.
2. Data Description
Three different time series, electrical conductivity measurements (ECM), dielectric properties (DEP) and ion chemistry (SO4 2¯) from one medium-length (~2500 years; 160 m) ice core, have been used to implement the techniques (Fig. 1). The solid conductivity of the ice cores has been measured with ECM (Reference HammerHammer, 1980) and DEP (Reference Moore and ParenMoore and Paren, 1987; Reference Moore, Mulvaney and ParenMoore and others, 1989; Reference MooreMoore, 1993; Reference Wilhelms, Kipfstuhl, Miller, Heinloth and FirestoneWilhelms and others, 1998). The measurements were sampled semicontinuously, with an interval of 2 mm for the ECM and 5 mm for the DEP. They were performed in an excavated freeze laboratory at the drilling site. The DEP measuring electrode was 10 mm and the measurements were performed at 250 kHz (Reference HofstedeHofstede and others, 2004). Both ECM and DEP measurements have been normalized to –15°C. The sulphate data were sampled adjacently with a length of 50 mm, and the sulphate content was determined by ion chromatographic analysis at the Alfred Wegener Institute, Bremerhaven, Germany. For details on the measurement set-up see Reference Traufetter, Oerter, Fischer, Weller and MillerTraufetter and others (2004) and references therein.

Fig. 1 Raw data of sulphate, DEP and ECM used to evaluate the compared methods (Reference HofstedeHofstede and others, 2004).
In this study, ECM represents a densely sampled signal with a low-frequency trend and low signal-to-noise ratio (S/N). That is, relatively high noise is obscuring the dynamical part of the signal. DEP represents a densely sampled smooth signal with high S/N. The low-frequency trend in the ECM signal is probably an effect of increased density down-core. The raw DEP record shows a similar low-frequency trend, but since the relation between ice capacitance and density is relatively well understood it has been corrected for.
The sulphate data are derived from samples cut from the ice core, and each piece represents a data point, so they are not as densely sampled as the electrical data. This way of sampling leads to a low-pass filtered version of the underlying sulphate signal.
3. Criteria for Threshold Selection
In this section, we present five different techniques for determining thresholds for peak detection in ice-core records. The first three techniques use all the available data to estimate a global threshold, whereas the latter two techniques are based on local estimation of the threshold via windowing and local smoothing.
In four of the techniques a bandpass filter operation is performed before the statistical test is applied. This is done to improve the S/N, to eliminate natural and measurement- induced variations in background values with time. This operation is important for data sampled semi-continuously like the DEP and ECM. For sampling techniques where adjacent samples of a finite (longer) length are obtained, the sampling procedure naturally performs a low-pass filtering. Due to this low-pass filtering, some of the noise artefacts have been removed. The purpose of the bandpass filtering process is to enhance the features of interest by blocking short and long wavelengths.
Technique I: normalized amplitudes
This method has previously been described in Reference Karlo¨fKarlöf and others (2000) and applied in Reference Karlo¨fKarlöf and others (2005). The records were first low-pass filtered, then we subtracted the low-pass filtered data from the original data, thus creating de-trended, high-pass filtered versions (Fig. 2). A first-order Savitsky–Golay filter was used because of its documented good performance in retaining peaks when smoothing data (Reference Press, Teukolsky, Vetterling and FlanneryPress and others, 1992). This removes unknown low- frequency relationships, such as the density effect on the ECM signal in the measurements (Reference Karlo¨fKarlöf and others, 2000). Finally, the residual was low-pass filtered at a higher cut-off frequency (called high-pass filter in Reference Karlo¨fKarlöf and others, 2000), and the bandpassed output was used for further analysis (Fig. 2). This bandpass routine has been used for all methods except method V. The output was then normalized to one standard deviation (1σ), and peaks having positive amplitude over 2σ were considered for dating purposes. This technique is adapted from Reference DelmasDelmas and others (1992), Reference MayewskiMayewski and others (1993), Reference ZielinskiZielinski and others (1994) and Reference Cole-Dai, Mosley-Thompson and ThompsonCole-Dai and others (1997), and defines a volcanic signal to be a spike larger than the normal background, i.e. mean plus standard deviation. The filtering technique described is different from that used in the other studies. The variance (σ 2) is estimated as the mean squared deviation from the mean, and the whole dataset was included in estimating the variance, i.e. the peaks were not omitted. This leads to an increase in σ and therefore a higher and more conservative threshold value. Thus, we can summarize the test in the following way: the significant threshold (ST) is

Fig. 2. (a) The original data (light shade) and its low-frequency component (black). (b) The high-pass residuals (light shade) and the Savitsky–Golay bandpass filtered residual (black).
where ![]() is the mean of the bandpass filtered signal xs and σs is the estimated standard deviation of xs.
is the mean of the bandpass filtered signal xs and σs is the estimated standard deviation of xs.
This method has proven successful, but the fact that we are not correcting for multiple testing, and that we need to make a subjective decision on the best smooth, can be considered as weaknesses. The method is also biased since we are assuming more or less the same amplitude of the episodic events throughout the period covered.
When many hypotheses are tested (multiple testing), the probability of falsely rejecting the null hypothesis (e.g. erroneously detecting a peak) increases sharply with the number of hypotheses. The number of hypotheses in our case is the number of samples in the dataset. An unguarded use of single-inference procedures, where we control the level of the test for each single test, results in a greatly increased false-significance rate when the number of tests is large. This is the problem of multiple testing, and instead of controlling the level for each test, one would like to control the false rejection of the null hypothesis for the entire collection (or family) of tests that makes up our experiment.
Technique II: normalized amplitudes using a difference variance estimate and correcting for multiple testing
This technique involves the same smoothing operation and test statistics as for technique I, but with a correction of the significance level since multiple testing is performed. Moreover, a new, more conservative way of calculating the variance (Var(xi)), is presented. In our new procedure, this variance is related to the difference between values of adjacent indices, Var(x i – x i’1).
We have:
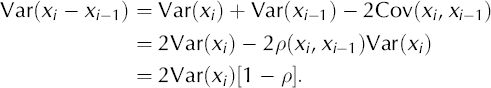
Thus, it follows from Equation (2) that
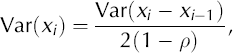
where the autocorrelation ρ is estimated from x. The technique relies on applying Equation (2) in an area of the time series where the adjacent differences of neighbouring values are due only to noise, and no peaks are present. The method presented in Reference Godtliebsen and Øigård.Godtliebsen and Øigard (2005) suggests how this can be done, and we use their suggestion to obtain a global estimate of the variance of x;, i.e. Var(x;). Thus, Var(x;) = σ2 and the threshold STÜ is found by correcting the threshold level for multiple testing with the assumption of a normal distributed error term
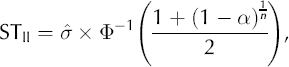
where ϕ–1 is the inverse of the normal distribution and n is the number of observations in x. As discussed in section 4, the assumption of normal distribution can be strengthened by taking the logarithm of the time series.
The rationale for correcting for multiple testing is as mentioned above, based on the assumption that the more tests we perform, the more likely it is to erroneously detect a peak.
Our hypothesis test is based on testing
H0: the peak amplitude is not significantly higher than the background
against the alternative hypothesis,
H1: the peak amplitude is significantly higher than the background.
We define α as the probability (P) of falsely rejecting the null hypothesis. Namely,
Consequently,
When performing multiple tests we define the following events:
where n is number of tests performed and, hence, equal to number of observations in x. To obtain an overall significance level equal to α when n tests are performed, we must have
If we assume that the tests are independent, we have
For each test we have
Hence, it follows that
which means that
Thus, for each test we use, under the assumption of a normally distributed error term, the quantile
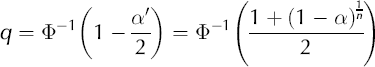
will be the new quantile which corrects for multiple testing. Here n is the number of tests, and n is the number of observations in x in this case (Reference Chaudhuri and MarronChaudhuri and Marron, 1999).
The variance calculated this way is lower than the variance calculated in technique I. Note, however, that by correcting for multiple testing, a threshold, motivated from more accepted principles in statistics, is achieved (Fig. 3).

Fig. 3. Example of bandpassed version of the Savitsky–Golay filtered sulphate data. The horizontal line indicates the level of the threshold as estimated with technique II. All peaks having amplitude over the threshold are considered.
Technique III: normalized amplitudes using median variance estimate and correction for multiple testing
A robust way of estimating the variance is to estimate it via the median, i.e.
and then correct for multiple tests in the following way:
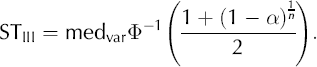
Here n has the same interpretation as in Equation (7). This estimation of the variance has been used previously in geophysical applications to detect volcanic peaks in nonsea-salt sulphate records of Greenland ice cores (e.g. Reference Fischer, Wagenbach and KipfstuhlFischer and others, 1998). However, they did not correct for multiple testing. Moreover their method was applied as a running analysis only on data with a high S/N (see method IV). Their method can be summarized as
where runmed is a running median filter, k is an empirically found parameter and should be compared with Equation (7), and MAD is the same as medvar. Thus, instead of using a Savitsky–Golay bandpass filter they used a low-pass median filter.
Technique IV: a local window version
By applying either technique II or III locally, we obtain techniques that circumvent problems with non-stationarity in variance leading to a biased threshold towards higher peaks and thus rejecting peaks of less magnitude (Fig. 4). These smaller peaks may also be significant but they might have a smaller magnitude due to the way they have been recorded in the snow. This might be explained by changes in snow deposition pattern over time. This process is something techniques I–III do not account for.

Fig. 4. Technique IV applied on bandpass filtered DEP data. Again all peaks having amplitude over the wiggly line are considered. Technique III is used within the window to do the statistical inference.
Here we propose a technique based on a rectangular window of a certain size that is run over xs, and the variance and threshold is estimated within the window in the same way as described in Equations (8) and (9). However, n now represents the part of xs contained in the window. The major disadvantage of this technique is the loss of data at the start and end of the time series. One way to partially circumvent this is to pad mirrored versions of x and run the window over the ‘edges’. Of course the threshold will be affected by the end effects, but the threshold obtained will aid in guiding the analyst’s interpretation of these areas. The influence of end effects on the threshold will not reach further into the record than the window length at each end. Moreover, the influence decreases with distance from the start and end. When choosing the window length, the following considerations should be accounted for: First, sufficient data points need to be covered in the window to allow for proper statistics. As a rule of thumb, we suggest that the window should always be greater than 30 observations. Second, the length of the window should be shorter than the distance between two adjacent peak events of the record. This minimizes the risk of biasing the threshold due to adjacent peaks of different amplitude.
Technique V: scale-space analysis of ice-core records
In this technique the estimation of variance for the threshold determination is replaced by an estimation of the significance of the derivative. A peak is defined where the sign of the derivative is changed more or less simultaneously over a number of scales. We apply a scale-space technique described in Reference Godtliebsen and Øigård.Godtliebsen and Øigård (2005) to analyze the ice-core records. The technique first obtains a family of smoothed estimates of the ice-core records for various degrees of smoothing. Next, the derivatives of the estimates are studied, and the testing is now concerned with whether the derivative of a smoothed estimate has zero crossings, i.e. the sign of the derivative is changed. When the derivative is significantly greater than zero, this means that the ice-core records are increasing. When the derivative is significantly below zero, the ice-core records are decreasing. When the derivative is not significantly different from zero, the ice- core records are flat. A peak is detected where the sign of the derivative is changing for estimates of various degrees of smoothing. We will not go into detail concerning the method, but only give an outline of the procedure. See Reference Godtliebsen and Øigård.Godtliebsen and Øigård (2005) for a thorough description of this technique.
The procedure is as follows:
Obtain smoothed estimates of the ice-core record.
Estimate the derivative of the ice-core time series over several scales. In this case the physical scale is in metres along the ice core.
Perform statistical tests on the derivative to check whether it is greater than zero, below zero or not significantly different from zero.
The above-mentioned procedure is repeated for a whole range of different degrees of smoothing (scales). The idea is to view the ice-core time series at different degrees of resolution. For small smoothing parameters, i.e. small scales, we zoom into the ice-core time series and investigate local behaviour, i.e. short time-scales. For larger smoothing parameters, i.e. large scales, we zoom out of the ice-core records and investigate the global behaviour, i.e. the overall trend of the time series. The output of the method is a feature map, which is a greyscale map as a function of location (time) and scale (degree of smoothing) (Fig. 5). This feature map is a graphic illustration of the dynamic behaviour of the ice-core records, and can be interpreted as follows. When the derivative is significantly greater than zero, the feature map is flagged black at this particular location and scale. When the derivative is significantly below zero, the feature map is flagged white at this particular location and scale. When the derivative is not significantly different from zero, the feature map is flagged grey at this location and scale. Thus, a peak will be detected in the areas where the map shows a transition from black to white.

Fig. 5. Highlighted section of the result from implementation of technique V on the DEP record. (a) A family of smoothed records. (b) Areas of significant positive or negative derivative as function of depth and scale. Dark grey indicates significant positive, light grey indicates significant negative and white indicates derivative not significantly different from zero. A peak is defined in the transition from dark grey to light grey, and the transition has to be clear over several scales (ß) (Reference Godtliebsen and Øigård.Godtliebsen and Øigard, 2005).
4. Results, Discussion and Evaluation of Performance
When evaluating the technique the following criteria were considered:
-
1. Number of peaks identified by the technique.
-
2. The ability to find ‘known’ peaks in the datasets.
For the technique to perform satisfactorily we decided that it should be able to detect the peaks of Krakatau, Indonesia (AD 1883), Tambora, Indonesia (AD 1815), the quadruple peak around AD 1254 and the large-amplitude peak dated to 364 BC (Reference ZielinskiZielinski and others, 1994). In the current datasets this corresponds to depths of 12, 18, 57 and 147 m respectively. In general, there are four factors that determine the amplitude of the signal peak recorded in an ice core:
-
1. Strength of source. The signal needs to be strong enough to change the local atmospheric concentrations in order to make a significant imprint in the record.
-
2. Short residence time to create localization in the peak. Longer residence times might be recorded as a trend rather than a peak since the fallout time is extended with longer residence time in the atmosphere.
-
3. Deposition of particulate needs to occur at the drill site during the atmospheric residence time.
-
4. Limited post-depositional redistribution of the snow. Post-depositional redistribution may either erode the snow in which the signal is contained or lead to a mixing of snow from different precipitation events. Both processes may lead to a decrease in amplitude.
Techniques I–III provide different ways of estimating the variance of the dataset. Techniques II and III also correct the threshold for multiple testing. The techniques that use all the data are sensitive to long-period trends. This is partly handled by the elimination of trends through bandpass filtering of the data prior to analysis. This is one major disadvantage of these techniques, as successful bandpass filtering of the input data before the analysis is dependent on the user’s knowledge of the dataset. If the peaks in the dataset are of variable amplitude, the first three methods are biased towards selecting large-amplitude events. There are variations in the level of estimated threshold values between methods I–III and the respective data series (Table 1). The reason for this variation is that the error or noise term in the respective data series influences the determination of variance in each method. The low-S/N ECM signal gives lowest ST by technique I and highest by technique III, whereas for the high-S/N signals like DEP and sulphate the picture is reversed. Technique II has a ST between III and I for all three data series. That is, how conservative a method is with respect to ST is determined by the noise characteristics of the recorded signal under consideration. Technique II seems to be least susceptible to this effect (Fig. 3).
Table 1. Summary of significant thresholds (ST). Note the differences in threshold level due to how the different types of recorded signals interact with the threshold estimation

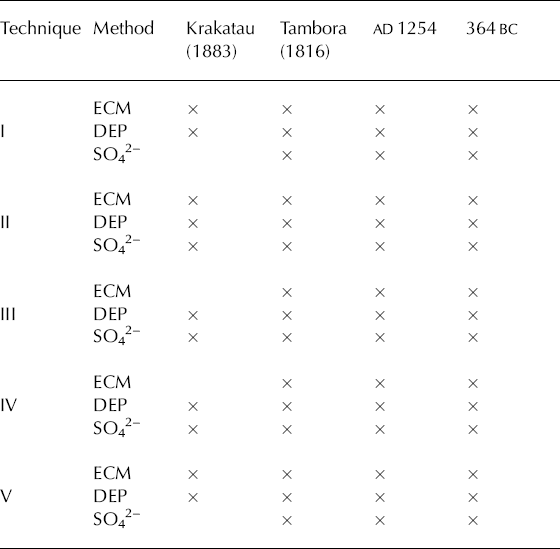
A more important comparison than the ST level, and which also allows comparison with the other two methods, is the number of peaks detected and the ability to detect defined reference peaks. For techniques I–III the number of detected peaks is directly related to the threshold level (Table 2). However, the detection of the defined reference peaks indicates the ability to detect peaks of variable amplitude. The reference peak with the smallest amplitude (Krakatau 1883) is the one that is missed by techniques I, III, IV and V, but not in all three records (Table 3). The reason why technique II captures this peak in all three records is simply the low variability of threshold level compared with I and III.
Table 2. Number of peaks identified by each method
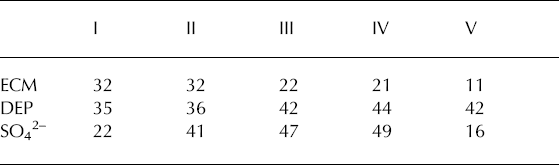
Table 3. Compilation of identified reference peaks. Note that only technique II identifies all reference peaks in all three types of records. Only the reference peak with the smallest amplitude falls out
Technique V identifies a similar number of peaks in DEP to the other techniques. This is not the case for the sulphate data, probably because of their smaller sample size. As mentioned before, each sample of the sulphate data is a mean value over a finite length (5 cm) of the ice core. This gives fewer samples along the record, but each sample has a higher ‘degree of freedom’ (df). A mean of several samples has higher df than each individual sample contributing to the mean. Technique V does not take this into account, but treats the data as if they consist of a lower number of samples. This leads to the possibility of fewer peaks being identified. This effect is naturally handled by the other techniques that base the threshold on the variance, as the variance naturally decreases with longer samples (higher df per sample), or, more precisely, low-pass filtering with lower cut-off frequency gives lower variability for this type of signal. Technique V does not work satisfactorily on the low- S/N record represented by ECM data. Many peaks are not well defined, probably for two reasons. First, as there is more noise in these data it is naturally more difficult to define a significant slope of the derivative. Second, as this dataset is sampled very densely, not only does it contain more high- frequency noise but also the peaks are not as sharp as those of a dataset containing fewer samples. This also leads to less defined peaks in technique V. Technique IV (Fig. 4) is the least conservative method with respect to the number of peaks identified, whereas V is the most conservative for records of fewer samples as well as for the low-S/N ECM record.
The sulphate and DEP records are weakly log-normal distributed (Fig. 6). Thus, by log-transforming these data the assumptions of normal distribution are strengthened. For technique I this results in less conservative thresholds, with more peaks identified. Techniques II and III are more conservative and thus identify fewer peaks. However, the reference peaks are all identified. As anticipated, technique IV shows, within the window, the same pattern as techniques II and III. The performance of technique V is not changed for the log-transformed DEP records compared to the non-transformed data, whereas for the transformed sulphate data it fails. This is probably due to the influence of low S/N or low sample rates, both of which contribute to the difficulties in defining significant derivatives.

Fig. 6. Distribution of the DEP data with a normal distribution fitted to the data (solid line). Note the tail towards higher values which indicate a logarithmic distribution. Taking the logarithm of the data gives a more normal distribution.
Techniques I–III are very quick and easy to implement, and no subjective choices need to be made except for the bandpass filtering. However, they suffer from the fact that they take all the data into account in the variance estimate, and thus are somewhat biased towards large-amplitude peaks. Technique IV suffers slightly from a longer computational time and the additional decision on the optimal window size, whereas technique V is computationally slow for large datasets and dependent on ‘large’ transitions in the values to efficiently define the position of zero derivative of the peak. Another disadvantage with technique V is that asymmetric peaks with a long tail (on the ‘younger’ side) might hamper its ability to define a significant slope of the derivative. However, the idea of looking for significant peaks at several time-scales, not only the scale defined via a static filter routine as for the other techniques, the colour map presentation (Fig. 5) and the ability of the method to take the shape of the peak into consideration are compelling aspects of the scale-space approach.
It should also be noted that a direct implementation of a derivative method like SiZer (Reference Chaudhuri and MarronChaudhuri and Marron, 1999) has been tried. However, it did not yield satisfactory results, primarily because the events we are trying to identify are present on such short scales that proper analysis of the significance of the slope of the derivative is prevented.
All the techniques reveal whether a peak deviates significantly from the background. Only technique V takes into account the shape of the peak. Further, no inference is made on the origin of the peak. Knowledge of the underlying physical process is required to assess correctly the significance and origin of the peak. Peaks found in time series such as those used in this study are believed to have a volcanic origin (Reference HammerHammer, 1980; Reference Moore, Mulvaney and ParenMoore and others, 1989; Reference ClausenClausen and others, 1997). However, to be able to address that question, other methods need to be used based on historical data on eruptions, location and magnitude of source (Reference Delmas, Legrand, Aristarain and ZanoliniDelmas and others, 1985) and trace element analyses of fine ash (Reference Palais, Kirchner and DelmasPalais and others, 1990). In addition, only peaks that are identified in all of the available records should be considered (Reference ZielinskiZielinski and others, 1994; Reference Karlo¨fKarlöf and others, 2000).
5. Conclusion
Five techniques for determining significant peaks are compared. Technique II shows less variation in its estimates of threshold than techniques I and III. Techniques I–III are easy and quick to implement, once the data have been bandpass filtered. Technique IV is a local implementation of II and III, and is preferred if one assumes that the record is affected by changes in variance over time (non-stationarity in variance). Technique V is recommended when one considers the shape to be more important than the amplitude of the peak;however, one drawback is the long computational time compared with the other methods. For most situations technique II or III is recommended.
This study has shown that there are obvious advantages in using a statistical approach to find peaks in ice-core records. A further advantage if such methodology can be standardized is that intercomparison of different ice cores can be done much more accurately than today. Moreover, since the methods we have compared identify different numbers of peaks, it is important to use patterns of several peaks when trying to line up events between different stratigraphy records.
Acknowledgements
The scientific editor D. Peel and two anonymous reviewers are thanked for helpful comments on the manuscript. J.-G. Winther, E. Isaksson and R. van de Wal are also acknowledged for insightful comments. This work is a contribution to the ‘European Project for Ice Coring in Antarctica’ (EPICA), a joint European Science Foundation (ESF)/European Commission (EC) scientific programme, funded by the EC and by national contributions from Belgium, Denmark, France, Germany, Italy, the Netherlands, Norway, Sweden, Switzerland and the United Kingdom. This is EPICA Publication No. 135. The Norwegian Polar Institute and the Research Council of Norway have funded the work.











